このページは、令和2年4月24日に一部更新しました。
![]()
ここで、狭義の分散分析すなわち1変量分散分析に戻ると、狭義の意味における 分散分析にも大きな広がりがある。この広がりを一瞥する前に、分散分析、ひいては 実験計画法の基本的原則を示しておこう。つぎに示すのは、Fisher の提唱した 実験計画法の3原則である。
|
さて、最も単純な完全無作為化法 (completely randomized design) の 場合で上の問題を説明しよう。この場合、3原則のうち最初の2つのみ が満たされる。以下に、Kirk (1982) の用法に従って、以降この計画法を CR-p デ ザインと書くことにする。CR-p デザインでは、水準の数 p は2以上である。 研究者は、従属変数に影響すると考えかつ最も重要であると考える1つの因子 を取り上げ、従属変数に関して均質な無限母集団からの独立で無作為なN 個 の標本のそれぞれを、設定した p 水準のいずれかに無作為に割り付ける必要 がある。
つぎに、因子数が2つ以上の実験は、多因子実験 (multi factor experiment) と呼ばれるが、とりわけ取り上げた因子の水準のすべての組み合わせを1回以上実験 するものは、一般に 要因実験 (factorial experiment) と呼ばれる。もし、 CR-p デザインを2つ以上の因子の場合に拡張するとすれば、そのような実 験は完全無作為化要因デザイン (completely randomized factorial design) と 呼ばれる。とりわけ、因子が2つの場合は、2処理(因子)完全無作為化要因デザイ ン (completely randomized factorial design with two treatments) と呼ばれ る。Kirk (1982) に従えば、これは CRF-pq デザインと表記される。
例えば、2処理 (因子) 完全無作為化要因デザインの2因子の水準がそれぞれ p 及び q であるとする。この時、2因子の処理のすべての組み合わせの数 すなわちセルの総数は、pq となる。このデザインでは、われわれはこれらす べてのセルに対してそれぞれ等しい被験者数r を考えるとすれば、これらのセ ルに対してpqr 人の被験者を完全に無作為に割り付けなければならない。
因子数がいくつであれ、完全無作為化デザインでは、従属変数に影響しなおかつ 研究者が関心のある要因間に重要度の強弱はない。これに対して、それらの間に 強弱があり、因子のなかに当面の主要な関心がない因子、すなわち局外変数 (より、 正確には、nuisance parameter 局外母数という) が存在 する場合には、Fisher の実験計画法の3原則のうちの最後の局所管理の原則を 取り入れて、局外変数の幾つかの水準内では局所的な均一化を計るとよい。
そのためには、あらかじめ無作為抽出された被験者を局外因子の複数の水準ごと に仕分けしておき、つぎに局外因子のそれぞれの水準ごとに複数の被験者を主要 な関心のある因子の各水準に無作為に割り付ける。このようなデザインは、 乱塊 法 (randomized block design) と呼ばれる。 Kirk (1982) に従えば、このデザ インは、RB-p デザインと表記される。
RB-p デザインでは、通常主要な因子と局外因子の交互作用はない、もしくは無視 できるという前提がある。この前提が疑われる場合は、局外因子(ブロック因子)の 水準ごとに、主要因子の各水準に対して同数の被験者を割り付ける。このデザイ ンは {\gt 一般化乱塊法} (generalized randomized design) と呼ばれ、GRB-p デ ザインと表記 される。一般化乱塊法デザインは、形式上は CRF-pq デザインと同一であるが、完全 無作為化要因デザインの場合と異なり、被験者は局所管理されたグループごとに主要 な要因の各水準に無作為に割り付けられる点に注意が必要である。
RB デザインで主要な因子が2つ以上の場合は、一般に乱塊要因デザイン (randomized block factorial design) と呼ばれる。例えば、それが2つ のデザインは2処理(因子)乱塊要因デザイン (randomized block design with two treatments, 又は a two-treatment randomized block design) と呼ばれ、 Kirk 流には RBF-pq のように表記される。ここで、p 及び q は、各 主要因子の水準数である。
RBF-pq デザインでは、あらかじめ無作為抽出された被験者を局外因子の複数の 水準ごとに仕分けしておき、つぎに局外因子のそれぞれの水準ごとに複数の 被験者を主要な関心のある因子の組み合わせによりできるpq 個の水準に無作為 に割り付ける必要がある。
RB-p デザインも RBF-pq デザインも共に、局外因子は1つであった。これを 2つ以上考える1つの方法が、分割区画デザイン (split-plot design) であ る。その最も単純なケースが、Kirk (1982) に従えば、SPF-p.q デザインである。この デザインは、 RB-q デザインが p 個あるケースと考えることもできる。
![]()
SPF-p.q デザインでは、原則として、従属変数に影響する2つの主要因子と
2つの局外因子を考える。また、主要2因子には研究者の関心に強弱があるものと
する。ここで、それらをA因子、B因子とし、研究者は A因子の方の効果には
あまり関心がなく、B因子の効果及びA因子とB因子のからみの効果に関心が強い
とする。
このような場合、われわれはまず(原則的には無限母集団からの無作為標本 としての)被験者を、第1局外因子の水準による p 個のブロックに仕分けし、 さらにそれぞれのブロックを、第2の局外因子の水準により r 個のブロックに 仕分けし、それらの1つ1つは q 人の被験者から成るとする。
SPF-p.q デザインでは、この時まずA因子の p 個の水準に、第1局外因子の 水準から成る p 個のブロックを無作為に割り付ける。つぎに、A因子のそれぞ れの水準ごとに、第2局外因子の r 水準の各々に仕分けられたq 人の 被験者を、 B 因子のq 個の水準に無作為に割り付ける。
例えば、 A因子はミラーリエル錯視の斜線分の長さのp 水準から成り、 B因子は斜線分の角度のq 水準から成り、第1局外因子は被験者の知能レベルの p 水準から成り、第2局外因子は当錯視の練習回数のr レベルから成 るとする。この時、われわれはまずA因子である斜線分の長さのp 水準に、第 1局外因子である被験者の知能レベルp 水準を無作為に割り付ける。つぎに、 A因子のそれぞれの水準に割り付けられた qr 人の被験者を、第2の局外因子 である練習回数のr レベルごと、q 人の被験者をB因子すなわち斜線分 の角度のq 水準に無作為に割り付ける。
SPF-p.q デザインでは、いつもこのように2つの局外因子が全く異質なもの である必要はない。例えば、農場における施肥の効果を見る実験では、例えば 農場をまず大きな区画にわけ、さらにそれぞれを隣接した下位区画に細分する。 そして、そこでの大区画を第1局外因子、下位区画を第2局外因子と見做すことが ある (奥野ら、1975)。
いずれにせよ、このようにして得られる SPF-p.q デザインでは、A因子の効果と第
1局外因子の効果は、完全に交絡している (completely confounded)、従って
両者は識別不可能である。しかし、一方では SPF-p.q デザイ
ンでは、一般に効果に関する検定での検出力は、B 因
子及び A 因子と B 因子のからみについては、A 因子のそれに比べて高いこと
がわかっている。
![]()
実験計画法では、うえのようなオーソドックスなデザインのみならず、実験の 日時を短縮したり、少ない被験者で結論を得るために上述のデザインを変形する ことも多い。例えば、CRF-pq デザインではセルの総数はpq 個に、CRF-pqr デ ザインではセルの総数は pqr になる。セルの総数が多くなると、実験の費用や 時間がかかること以外に実験条件の均一化が一般に困難になる場合が出てくる。 これらの難点を克服するための1つの方法が因子数3の場合のラテン方格法 (Latin square) である。
ラテン方格法では、3因子の水準がすべて同じでなければならないという制約が あるが、それを p とすれば、CRF-ppp デザインでは p3 個のセル が必要なのに対して、この方法では、それを p2 個、すなわち 1/p で済ませてしまうことができる。Table 1.1 は3つの因子 A、B、C が すべて4水準から成る場合のラテン方格の1つの例である。セルの数は、CRF-444 デ ザインの場合、43=64 必要なのに対して、その4分の1の 16 個で済ませる ことができる。
| 因子・水準 | B1 | B2 | B3 | B4 |
| C1 | A2 | A1 | A4 | A3 |
| C2 | A3 | A4 | A1 | A2 |
| C3 | A4 | A2 | A3 | A1 |
| C4 | A1 | A3 | A2 | A4 |
ラテン方格法では、一般に3因子の水準数をすべて p として、つぎの制約を 必要とする:
ラテン方格法とよく似た方法に、グレコラテン方格法 (Graeco-Latin square) がある。この方法は、CRF-pppp デザインの場合、p4 個のセルを 必要とするのに対して、p2 個のセルで済ませてしまうことができる。
ラテン方格法は、主要な1つの因子に対して2つのブロック因子を構成する もう1つの方法とみることもできる。例えば、上の表で因子 A は主要因子、B 及び C 因子は共にブロック因子と見れば、ブロック因子構成のための1つの方法と みれる。同様に、グレコ・ラテン方格法は、主要な1つの因子に対して3つの ブロック因子を構成する方法ともみれる (奥野ら、1975)。
教育や心理学の分野では、これ以外にも複数の水準もしくは処理を、同一の 被験者が繰り返すようなデザインがよく用いられる。このようなデザインは、 反復測度デザイン (repeated measures design) とか反復測定デザイン (repeated measurement design) と呼ばれる。反復測度デザインは、上述の方法のうち、 ブロック因子を用いるデザインで、ブロック因子の各水準に各被験者を充てる ことによって、実現する。例えば、通常の RB-p デザインでは、被験者は 主要因子の水準数を p、ブロック因子の水準を k とすれば、pk 人必要なのに対して、反復測度 RB-p デザインでは、ブロック因子の各水準には各 被験者が対応するので、k 人で済むことになる。
反復測度デザインは、しかしながら、一方では同一被験者
が異なる水準に反応することにより、場合によっては F- 検定量もしくは t- 検定量に
ゆがみを生じさせるという弱点も持つ。
![]()
実験計画法の中には、上述のような比較的単純なデザイン以外に、例えば 釣り合い型不完備デザイン (Balanced Incomplete Block Design)、ユーデ ン方格法 (Youden square)、一部釣り合い型不完備デザイン (Partially Balanced Incomplete Block Design) など、複雑なデザインも考案 されている (奥野ら、1975)。
これまで、実験計画法の広がりをいろいろなデザインを紹介することにより
議論してきた。この議論を通じて、実験計画法というものは、
得られたデータを事後的に単に統計的に分析する方法ではなく、従属変数に影
響する因子の効果の有無を検討するために最初からデータの収
集方法まできちんと決めておく、体系的、組織的なデータの収集・分析の方法
である、ということに注意すべきである。
![]()
さて、上述の如何なるデザインに対しても、統計学ではそれに特有な構造模型 (structural model) を対応させる。構造模型は、当該デザインにより収集された 従属変数の値がどのような数学的な構造式により表現できるかを記述するもので ある。例えば、CR-p デザインの構造模型は、つぎのように書かれる:
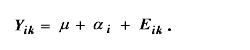
|
(1.1) |
ここで、例えば Yik は、当該因子の第i水準の第k被験 者の従属変数の値を実現値 (realization) とする 確率変数で、αi は第 i 水準の因子の効果 (正確には、のち に見るように主効果という)を、Eik は第 i 水準の第k 被験者の測定誤差を実現値とする確率変数を表す。
如何なるデザインでも、因子の効果は、各水準に対して1つづつ対応して いると仮定する。したがって、因子の効果がないという仮説 (帰無仮説)は、 その水準に対応した効果がすべて等しい、という表現をとる。
ところで、「各水準の効果がすべて等しい」という帰無仮説を表現する方法として、 実験計画法、とりわけ分散分析では2つの表現を考える。1つは、当該因子の各 水準の効果は定数であると見做される時で、この場合には帰無仮説は、それらの 水準の効果を α1、α2、...、αp として、
H0: α1=α2= ... =αp, (1.2)
のように表現する。このように、因子の効果を定数と考える構造模型は、 母数模型 (fixed-effects model) と呼ばれる。うえ の H0 が成り立つ時は、標本としての従属変数の値の各水準での平均 値間には差がないことが期待される。
これに対して、当該因子の各水準の効果は変量 (確率変数)と見做される時 には、帰無仮説は (1.2) 式の形ではなく、水準の効果 (仮にA因子の効果とする) が母集団では平均ゼロ、分散 σA2 なる 正規分布 (normal distribution) (これは、統計 学では N(0, σA2) と書く)に従うと仮定し、その結果と して帰無仮説は、
H0: σA2=0, (1.3)
と書く。この場合の構造模型は、変量模型 (random-effects model) と呼ばれる。
どちらの模型を考えるかは、研究仮説の内容により変る。また、場合によっては 構造模型の右辺の誤差項を除く部分の要素が母数と確率変数の両方が混在する デザインを考えることもある。このようなデザインは、 混合模型 (mixed model) と呼ばれる。
最後に、分散分析では通常つぎの3つの仮定がなされることに注意しよう。
|
しかし、通常の分散分析では因子の効果を検討する F- 検定量は、正規性や等分
散性のくずれに対してはかなり頑健であるとの研究がなされている。ただしこれらの
仮定も、如何なる崩れに対しても F-検定量が頑健である、と
までは言えない ことにも注意することが必要である。例えば Pearson (1931)
は、F-検定量は正規性仮定からの適度の乖離に関してはたいへん頑健である、として
いる。また、 Lunney (1970) は、水準間でサンプル数が等
しいときは2値変数でも F-検定量は頑健であるが、サンプル数が異なる時には頑健で
ないとしている。
![]()
また、分散の 等質性に関しては、Box (1954a,b) や Cochran (1947) の研究からは、水準間で サンプル数が等しいときは、等質性からの適度な乖離に関してF-検定量は頑健である という結果が得られている。一方、Box (1953, 1954a) では、サンプル数が異な る時には、適度な等質性からの乖離しかない時でさえ、有意性検定への影響は 大であるという結果も得られている。
ここで、分散の等質性の検定には、これまで Bartlett (1937)、Hartley (1940, 1950) の方法、Cochran (1941) の方法、及び Box-Scheff\`e (Box, 1953; Scheff\`e, 1959) の方法が知られている。
また、上述の反復測度デザインでは、一般に反復測度因子の水準間では 同一被験者が反応することにより、従属変数の値は、独立性の仮定が損われ ることが多いので、後に見るように因子の効果を検討する F- 検定量や 水準間の平均値の比較時の F- や t- 検定量がゆがむ可能性がある。 このような場合には、そこで紹介するようにそれに対処するための何らかの 手立てが必要なことがある。さらに、反復測度デザインでは、通常の分散分析 ではあまり神経質にならなくてよい正規性からの乖離の影響が重大になる 場合もあり、注意が必要である。