一般に３つ以上の平均値の差の検定では、どの平均値間に差があるかを問題 にする。このような平均値間の差は、 対比(contrast) 又は 比較(comparison) と呼ばれる。対比（又は比較）のより正確な表現をするため、ここではまず、 分散分析モデルとして前節で述べた最も単純な完全無作為化デザイン(CR-Iデザイン) を取り上げてみよう。
例えば、Yを斜線分と主線分の角度を30度一定とした条件での
ミラーリエル錯視実験での錯視量で、I =3 で、
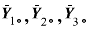は、それぞれ、斜線分の長さが、15mm、
30mm、45mm条件での錯視量の平均値であるとする。
この時、I 個の水準のそれぞれの従属変数 Y の平均値を
とする
と、それらは
|
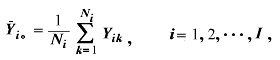
(1.13) |
と書ける。
一方、確率変数とその実現値（サンプル）を区別するために、 Yik の実現値を, yik と書くことにすると、標本平均は
|
(1.14) |
となる。この時
|
(1.15) |
|
(1.16) |
なる ψ が、対比の正確な定義である。
一方、対比 ψの推定値を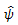 
と書くと、一般に
|
(1.17) |
となる。
上記のミラーリエル錯視で、(1.17) 式の対比の係数 c1 , ・・・ , cI を たとえば
|
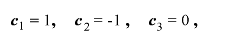
(1.18) |
とすれば、これは15mm条件と30mm条件の平均値間の 対比較 (pairwise comparison) であり、その推定値は、
|
(1.19) |
と書ける。
対比もしくは比較は、対比較のみに限定されない。たとえば、15mm条件と 30mm条件での錯視量の平均値と、45mm条件での錯視量の平均値との対比を考える こともできる。この場合、
|
(1.20) |
に取ればよく、その推定値は、
|
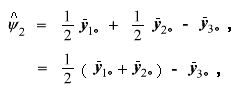
(1.21) |
と書ける。(1.21) 式のような対比は、 非対・比較 (nonpairwise comparison) と呼ばれる。
このように、一般に３つ以上の平均値について対比を考えると、たくさんの 対比を考えることができ、これらを総括的に 多重比較 (multiple comparison) と呼ぶ。
これらの対比相互の関係にかかわる重要な概念に、 直交対比 (orthogonal contrast) というものがある。ここで、つぎの２つの対比
|
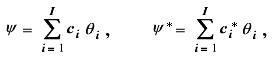
(1.22) |
を考えよう。ψの係数はc1 ,・・・, cI であり、
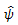の係数は
c1*,・・・, cI* である。この時、
２つの対比 ψ、ψ*は、
|
(1.23) |
又は
|
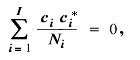
(1.24) |
を満たすとき、直交対比と呼ばれる。ここで、 釣り合い型デザイン (balanced design) とは、各水準のサンプル数がすべて等しいデザインであり、 非釣り合い型デザイン (unbalanced design) とは、各水準のサンプル数 が必ずしも等しくないデザインをいう。
たとえば、上記の(1.19)式及び(1.21)式の２つの対比
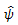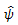及び 2
は、直交対比である。なぜならばそれぞれの対比の
係数(1.18)式及び(1.20)式で、N1 = N2 = N3 すなわち、
釣り合い型デザイン (balanced design) だとすれば、(1.23) 式を用いて、
|
(1.25) |
であるから。
一般に、I 
4
の時には、このような直交対比は無限に存在する。しかし、I個
の水準で１組の I -1個の直交対比 (I -1個の対比相互がすべて直交しているような
対比)を考えるとき、他の任意の直交対比 (の組み)は、その１組の直交対比の線形
結合 (重みづけ合計)により表現できることがわかっている。
ただし、一般に実験者は常に直交対比のみに関心をもつわけでもないし、 I -1個の直交対比に限定してもそれらのすべてに関心を持つわけでもない。
一方、(1.23) 式や (1.24) 式を満たさないような対比は、無限にあると いってよい。そのような対比は、 非直交対比 (nonorthogonal contrast) と呼ばれる。 たとえば上記のミラーリエル錯視で、(1.19) 式の対比に対して、
|
(1.26) |
なる対比
|
(1.27) |
を考えると、釣り合い型として、(1.23) 式を満たさないことは明白である。
対比についてのもう１つの重要な概念は、対比が実験の前にすでに確定している か否かに関するもので、どの対比を検討すべきかがあらかじめ決まっているような場 合、その対比は 計画的 (planned) もしくは 事前的 (a priori) で あるという。逆に決まっていない場合を、 非計画的 (unplanned) 又は 事後的(a posteriori 又は post hoc) という。
Kirk (1982)は、一般の対比を、つぎのように３分している：
|
これに関して、３つ以上の平均差の検定で、最初から検討すべき対比が決まって いる場合、 計画的検定 (planned test) という。一方、そうでなく、 全 体的F-検定 (overall F-test) を行い、要因の効果が有意な場合、すべての可能な 対比検定を行なう場合を 非計画的、事後的検定 (unplanned 又は a posteriori 又は post hoc test) と呼ぶ。