このページは、平成11年2月5日に開設しました。
このページは、令和2年4月24日に一部修正しました。
![]()
| 1. LSD 検定 |
| 2. HSD 検定 (Tukey法) |
| 3. SpjötvollとStolineのHSD検定の修正 |
| 4. Tukey-KramerのHSD検定の修正 |
| 5. Games-Howell法 |
| 6. Tamhane法 |
| 7. Scheffé のS法 |
| 8. Brown-ForsytheのBF法 |
| 9. Newman-Keuls法 |
| 10. Duncanの新多範囲検定 |
LSD検定 (the least significant difference test) は、Fisherが提案し たもので、まず全体的F-検定で帰無仮説 H0: α1=α2=…=αI の検定を行ない、有意差があるときのみ、すべての対に関する対比、すなわち対比較

|
(1.31) |
を考え、それが次式で与えられる 最小有意差 (least significant difference) を越えていれば、当該対比は有意とする方法である:

|
(1.32) |
ここで、tα/2, ν は、t-分布の上側 α/2 パーセント点の値であり、 νは UE の自由度である。又、Noは、釣り合い型デザインでの各グループ のサンプル数である。すなわちNo=N/I である。非釣り合い型の場合には、(1.32) 式の右辺のルートとしては、(1.28) 式のt の分母を用いる必要がある。
この方法では、全体的F検定は有意でも、対比較はいずれも有意でないということが 起こりうる。
HSD検定 (the honestly significant difference test) もしくは、 WSD検定 (wholly significant difference test) は、Tukey (1953) により 提案されたもので、各水準の標本数や母分散は同じと仮定さ れる。
HSD検定は幅広く使われているもので、 スチューデント化された範囲統計量
q (the studentized range statistic) の標本分布を用いる。q は、
及び
を、I個の
水準の平均のうち最大なものと最小なものとする時、

|
(1.33) |
と定義される。
q の分布では、UE の自由度 νと水準数Iが必要となる。LSD検定の (1.32) 式 に対応するHSD検定の場合の式、すなわち 臨界差 (critical difference) は、

|
(1.34) |
である。
最大なものと最小なものとの間で有意差があれば、さらにその範囲を1つづつ せばめて、同様な検定を行なう。その場合の q は、せばめたときの時の平均の 数に対応する qα と、もとの I の時の数の qα の平均とする。 α は、最初から 5 % なら 0.05 とする。
Ury (1976) は、非釣り合い型デザインの場合の事後的比較法間の 比較を行ない、標本数がほぼ同じ場合には、この方法 (Spjötvoll & Stoline, 1973) が最もよいことを示した。この方法は、Tukey のHSD 検定を一般化するもので、Tukey 法の (1.34) 式に当る臨界差は、
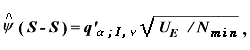
|
(1.35) |
とする。ここで、q'α; I, νは数表による。Nmin はI個の水準のサンプル数のうち、最小のものである。
非釣り合い型デザインで、水準間の標本数に開きがある時の 対比較には、Tukey (1953)とKramer (1956)によるTukey-Kramer法 がよいとされる。この場合、(1.34) 式のかわりに、

|
(1.36) |
を臨界差とする。Ni 及び Ni' は、対比較すべき2つの 水準数のサンプル数である。
ここまでに紹介した4つの方法は、通常の分散分析 (反復測度は含まない)の3つの仮定、すなわち正規性、等分散性、 独立性、の仮定をすべて満たすことが前提であるが、以下の2つの 方法は、等分散性が成り立たないか分散と標本数が異なる時に 頑健といわれている。
Games and Howell (1976)によるもので、臨界差は
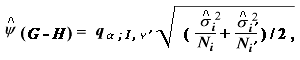
|
(1.37) |
を用いる。ここで、

|
(1.38) |
Tamhane (1977,1979) によるもので、臨界差は、
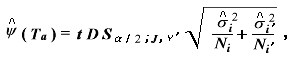
|
(1.39) |
を用いる。ここで、t DSα/2;J,ν' は、 J = IC2 及び Games-Howell法で定義される ν' ((1.38)式) に対して Sidák の乗法不等式 (the Sidák multiplicative inequality) を用いてt-分布から得られる値で ある。
Scheffé のS法は、Scheffé (1953)によるもので、全体的F-検定が有意ならば、 この方法は危険率 $\alpha$を一定に保ったままで、すべての事後的対比の評価が 可能となる。この方法は又、非釣り合い型デザインにも適用できる。ただし、 この方法は、たとえば対比較のための Tukey法 に比べて検出力は低いので、 Kirk (1982)は複雑な対比の評価の場合のみに勧めている。
この方法では、臨界差は、

|
(1.40) |
を用いる。ここで、
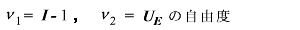
|
(1.41) |
Scheffé 法を、通常のF-検定として書くと、帰無仮説 ψ=0 を

|
の時、有意とすることに等しい (ここで、F 自身の自由度は ν1=1, ν2 = UE の自由度であることに注意!)。このことは、個々の対比の F-比 F1, ν2 に対して、帰無仮説のもとで

|
ならば、帰無仮説を棄却することに等しい。
![]() SAS では、contrast 文を用いた個々の対比の検定時に、F-値の検定には
族あたりの危険率をコントロールしていない。そこで、事後的非直交対比と見なされる
対比の場合には、うえの方法で族あたりの危険率をコントロールする必要がある。
ただし、そのためには竹内啓監修・高橋ら (1990, p.64) のように棄却点の数表
は見なくても、1.3.6 節に掲げたプログラムのように SAS を用いて検定すればよい。
SAS では、contrast 文を用いた個々の対比の検定時に、F-値の検定には
族あたりの危険率をコントロールしていない。そこで、事後的非直交対比と見なされる
対比の場合には、うえの方法で族あたりの危険率をコントロールする必要がある。
ただし、そのためには竹内啓監修・高橋ら (1990, p.64) のように棄却点の数表
は見なくても、1.3.6 節に掲げたプログラムのように SAS を用いて検定すればよい。
![]() SAS では独立測定要因の対比における対比平方和として、contrast 文によ
る F-検定における「Contrast SS」なる項が出力されるが、それはうえの
SAS では独立測定要因の対比における対比平方和として、contrast 文によ
る F-検定における「Contrast SS」なる項が出力されるが、それはうえの
ではなく、
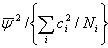
![]() 一方、SAS では反復測定要因の対比における対比平方和の場合、repeated
文もしくは manova 文の m= オプションで指定する対比の F-検定における平方和は、
個々の対比の誤差平方和が正規化される前のそれである関係上、
一方、SAS では反復測定要因の対比における対比平方和の場合、repeated
文もしくは manova 文の m= オプションで指定する対比の F-検定における平方和は、
個々の対比の誤差平方和が正規化される前のそれである関係上、
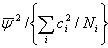
を掛けた
ものになっている。
BF法は、Scheffé のS法を修正するもので、Brown and Forsythe (1974)により提案された。彼らの方法は、Scheff\'eのS法以上に 分散の異質性に関して頑健であるという。この方法では、 臨界差は、

|
(1.42) |
を用いる。ここで、

|
(1.43) |
である。ただし、対比較の場合には、Games-Howell法やTamhane法の方が、検出力 が高い。
この方法は、Student(1927), Newman (1939), Keuls (1952)によるもので、 逐次手続き (stepwise approach) に基づく。まず標本平均 $\bar{y}_{1\bullet}, \bar{y}_{2\bullet}, \cdots,\bar{y}_{I\bullet}$ が小さい順に並べられる。そして、対比較はまずIステップ離れた 最大の平均差のある水準間で危険率$\alpha$で行なわれ、もし有意 ならば次にはI-1ステップ離れた次に大きい平均差のある水準間で 同じく危険率 $\alpha$で行なわれる、という形を取る。
Newmam-Keuls法は、釣り合い型デザインを仮定している 。 この方法での臨界差は、

|
(1.44) |
である。$\gamma$は当該対間のステップ数である。
Newmam-Keuls法の検出力は、Tukey法よりも高い。ただし、 この方法は実験ごとの危険率を$\alpha$に統制しない。
Duncan (1955)は、Newmam-Keuls法とよく似た事後的対比較の評価法を 開発した。この場合、rステップ離れた平均の対比較の危険率を、 $\alpha$ではなく、
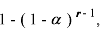
|
とする。
この方法での臨界差はNewmam-Keuls法と形式的には同じだが、 $q_{\alpha;\,r,\,\nu}$の値は彼の表を見なければならない。
Kramer (1956)は、Duncan法を非釣り合い型デザインの場合に 拡張する新しい多範囲検定を提案している。
最後に、統計パッケージプログラム SAS では、anova 及び glm の means 文のオプ ションとして、うえの方法のうち、1) LSD 検定(SAS 表記では LSD もしくは T)、 2) HSD 検定 (Tukey 法)とその非釣り合い型デザインへの修正(同 TUKEY)、 7) Scheffé の S 法(同 SCHEFFE)、9) Newman-Keuls 法(同 SNK、すなわち Student-Newman-Keuls multiple range test)、10) Duncan の新多範囲検定(DUNCAN) が利用可能である。
SAS ではこれらの他に、Gabriel 法 (Gabriel's multiple-comparison procedure, SAS では means 文の GABRIEL オプション) (Gabriel, 1978)、 Ryan-Einot-Gabriel-Welsch 法 (Ryan-Einot-Gabriel-Welsch multiple F test, means 文の REGWF オプション、及び 同 multiple-comparison procedure, means 文の REGWQ オプション) (Einot \& Gabriel, 1975; Ryan, 1959, 1960; Welsch, 1977)、対照群との比較のための Dunnett 法 (Dunnett' two-tailed t-test, means 文の DUNNETT オプション) (Dunnett, 1955) が利用 できる。
また、SAS では、上述のボンフェロニ手続き(BON)、及びシダークの修正手続き (SIDAK)も利用できる。ただし、これら計画的非直交対比も上の非計画的対比も 共に、SAS では区別せず並べているので、問題がなくもない。