このページは、令和2年4月25日に一部更新しました(数式を読みやすくしまし
た)。
![]()
完全無作為化2要因デザインの構造模型は、母数模型の場合次のように表わさ れる。
|
ここで、$\mu$は一般平均、$\alpha_i$は処理 A の第 i 水準の(主)効果、 $\beta_j$は処理 B の第 j 水準の(主)効果、$\gamma_{ij}$は処理 A の第 i 水準と処理 B の第 j 水準の 交互作用 (interaction)、Eijkは 誤差項である。また、

|
(1.46) |
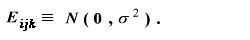
|
(1.47) |
帰無仮説は、次の3つである。

|
(1.48) |
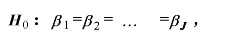
|
(1.49) |
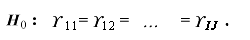
|
(1.50) |
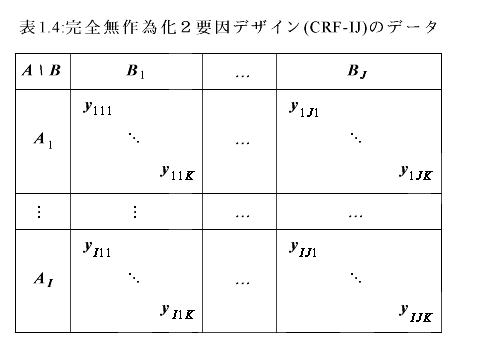
完全無作為化2要因デザインで釣り合い型デザインデータとその分散分析表は、 Table 1.4、1.5、及び 1.6 のようになる。 ここで、サンプル総数は、N=IJK である。
|

|

|

|
(1.51) |
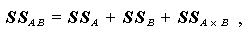
|
(1.52) |
また、

|
(1.53) |

|
(1.54) |
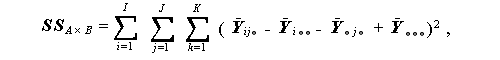
|
(1.55) |
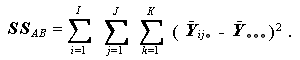
|
(1.56) |

|
(1.57) |
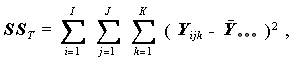
|
(1.58) |

|
(1.59) |

|
(1.60) |
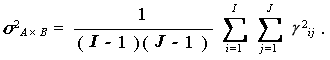
|
(1.61) |
完全無作為化2要因デザインで、たとえば処理 A の水準は母数、B の水準は 確率変数であるとすれば混合模型になる。この場合の構造模型は、次のよう になる。
|
ここで、$\mu$は一般平均、$\alpha_i$は処理 A の第 i 水準の(主)効果、 Bj は処理 B の第 j 水準による変動、Dij は処理 A の第 i 水準と処理 B の第 j 水準との交互作用変動、Eijk は誤差項(誤差変動)を表わす。 また、

|
(1.63) |
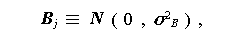
|
(1.64) |
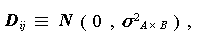
|
(1.65) |
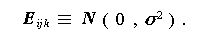
|
(1.66) |
(1.45) 式における母数模型の場合との違いに注意されたい。
データも、母数模型の場合の Table 1.4 と変わりないが、データの取り方が 異なること にも注意せよ。すなわち、この場合には、処理 B の J 個の水準は、たくさん 考えられるものの中から J 個を無作為に抽出しなければならない。
帰無仮説も母数模型の場合とは異なってくることに注意せよ。この場合、
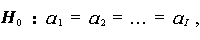
|
(1.67) |

|
(1.68) |

|
(1.69) |
さらに、分散分析表も Table 1.5 の母数模型の場合と変らないが、Table 1.6 の 平均平方の期待値は A,B,A\times B のところがつぎのように変る。

|
ここで、上の表における$\sigma_A^2$は、(1.59) 式で与えられる点で変らないが ここで、上の表における$\sigma_A^2$は、(1.59) 式で与えられる点で変らないが、 $\sigma_B^2,\sigma_{A\times B}^2$は、(1.60)、(1.61)式で与えられるのでは なく、(1.64)、(1.65)式の母数として与えられることに注意せよ。