このページは、令和2年4月25日に一部更新しました(数式を読みやすくしまし
た)。
![]()
この節では、交互作用の持つ意味について議論する。話を簡単にするため、 ここでは前節の母数模型の場合の交互作用を取り上げる。まず、交互作用がある ということは、(1.50) 式の帰無仮説が棄却されることである。このことは、IJ 個 の要素的交互作用 $\gamma_{ij}$ のいずれかがゼロでないということに他なら ない。これを明らかにするには、任意の要素的交互作用 $\gamma_{ij}$ がゼロと いうことの持つ意味が、まず明確にされなければならない。
そのためには、われわれは (1.45) 式の3つのパラメータ、$\alpha_i$、 $\beta_j$、$\gamma_{ij}$ を、セル(母)平均の言葉で書き換えたほうがわかり やすい。セル(母)平均とは、各セルの観測値の母平均であり、これ を $\mu_{ij}$ と表すとする。Table 1.8 は、CRF-IJ デザインにおける各セルの セル平均を表にしたものである。

|
この時、3つのパラメータはそれぞれつぎのように書ける:
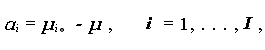
|
(1.70) |

|
(1.71) |
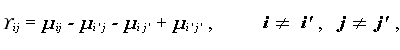
|
(1.72) |
\footnote{正確には、$\gamma_{ij}= \mu_{ij}-\mu_{i\bullet}-\mu_{\bullet j}+\mu$とかく。しかし、 すべての$i$、$j$についてこれが言える時、$\gamma_{ij}=\gamma_{i'j}= \gamma_{ij'}=\gamma_{i'j'}=0$なので、この時 $\gamma_{ij}*=\mu_{ij}-\mu_{i'j}-\mu_{ij'}+\mu_{i'j'}=0$となる。}
ここで、$\mu_{i\bullet}$、$\mu_{\bullet j}$はそれぞれ、処理水準 Ai 、Bj の観測値の母平均とする。
|
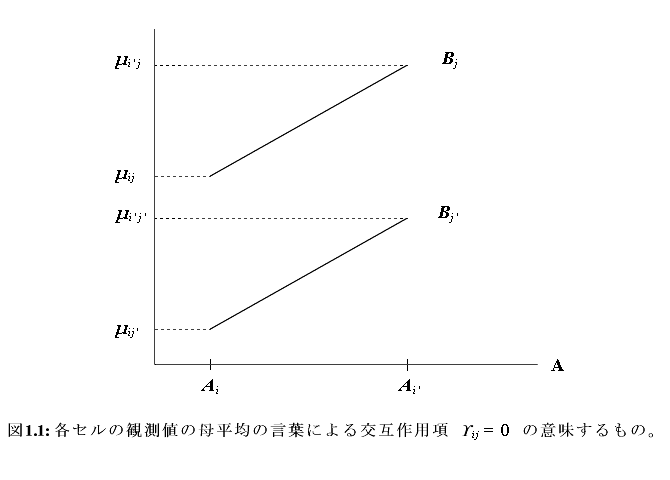
Fig. 1.1 は、要素的交互作用 $\gamma_{ij}$ がすべてゼロの時の、4つのセルの セル平均の例を示したものである。つまり、要素的交互作用 $\gamma_{ij}$ が ゼロということは、1つの因子Aの2水準 i 及び i' ともう1つの因子Bの 2水準 j 及び j' を取り上げた時、各々の対を結ぶ2つの線分が Fig. 1.1 の ように並行なグラフになることである、といえる。
このことは、言い換えれば、
| 要素的交互作用がすべてゼロということは、一方の因子の任意の2水準間での 従属変数の平均値の変化の仕方が、他方の因子の水準を変えても、変らない、 ということ |
|
(全体的)交互作用があるということは、一方の因子のいずれか1対以上の
水準間での従属変数の平均値の変化の仕方が、他方の因子の1対以上の水準間で
異なる、
|
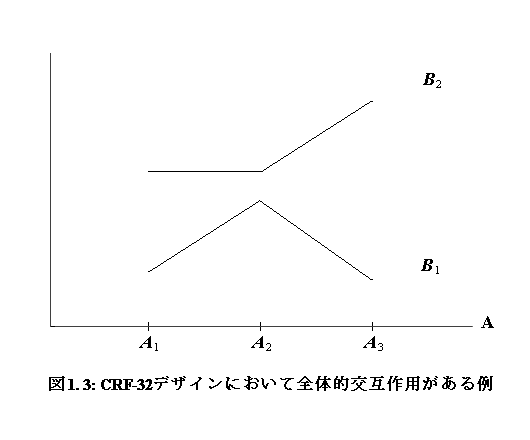
Figs. 1.2 及び 1.3 は、CRF-32 デザインで、それぞれ(全体的)交互作用が ないケース、及びあるケースを描いたものである。ここで、両図の縦軸は、共に 各セルの観測値の母平均であるとする。
Fig.1.2 のケースは、例えば因子A はミラーリエル錯視における斜線分の長さで、 15mm、30mm、45mm の3水準であるとする。一方、因子B は同錯視における斜線分の 角度で、15度、30度の2水準であるとする。この時、これらの2つの因子の水準 の組み合わせからなる6つのセルの観測値の母平均が、Fig. 1.2 のようであると する、すなわち(全体的)交互作用がない(1つの例)とする。このことは、 ミラーリエル錯視において、斜線分の長さを増大させると錯視量は増大傾向と なるが、この傾向はもう1つの因子の水準にかかわらず言える、ということを 意味する。言い換えれば、錯視量に対して2つの因子のからみの効果はない、 ということである。
他方、Fig. 1.3 のようなケースだとすると、斜線分の角度が 30度水準の 場合には錯視量は斜線分の長さを増大させると増大傾向となるが、15 度 水準の場合は必ずしもそうならない、ということである。つまり、この場合には 錯視量に対して2つの因子が複雑に絡んでいることを意味する。

|
|