このページは、令和2年4月25日に一部更新しました。
![]()
完全無作為化2要因デザインで交互作用が検出された場合には、どこにそれが 強く表れているのかをさらに詳しく検討したいことがある。この問題に対処 するために従来から知られている検定として、単純主 効果(simple main effect)の検定と、 処理-対比交互作用(treatment-contrast interaction)及び 対比ー対比交互作用(contrast-contrast interaction) の検定がある。脚注1
まず、単純主効果と通常の主効果との違いについて述べる。Table 1.8 を見れ ば明らかなように、通常の主効果は、(1.70)、(1.71)式にあるように、 2要因(処理)の場合には、各セルの観測値の母平均の言葉でいえば、それらの 行平均、列平均にあたるのに対して、単純主効果は、各行、各列ごとの各セルの 観測値の母平均にあたる。したがって、単純主効果は次の2種類になる:

|
(1.73) |

|
(1.74) |
そこで、単純主効果の検定のための帰無仮説は、I+J 個あり、つぎのように なる:
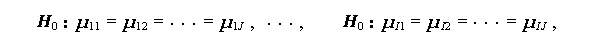
|
(1.75) |

|
(1.76) |

|
(1.77) |
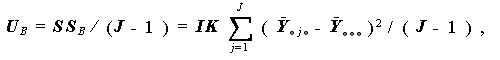
|
(1.78) |
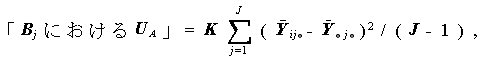
|
(1.79) |

|
(1.80) |
したがって、単純主効果の検定も兼ねた分散分析表は、Table 1.9 のようになる。

|
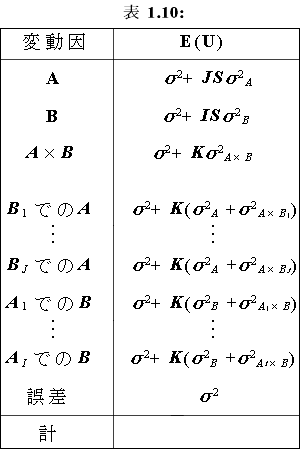
|
すなわち、
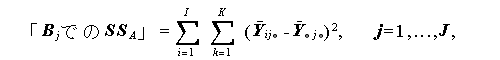
|
(1.81) |

|
(1.82) |
また、

|
(1.83) |
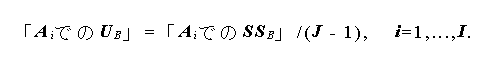
|
(1.84) |
さらに、
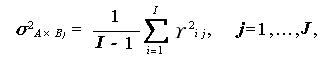
|
(1.85) |

|
(1.86) |
最後に、

|
(1.87) |

|
(1.88) |
単純主効果の帰無仮説が棄却される時は、当該行又は列の観測値の母平均の どこに差があるのかを検定する。
単純主効果の検定を用いた論文は数多く見られるが、上述の議論からわかるように、 全体的交互作用が有意でない場合にも、それらのうちの幾つかが有意になる可能性 がある。このことは、言い換えれば単純主効果は必ずしも全体的交互作用の 正確な下位検定にならないことを意味し、全体的交互作用仮説が棄却された時 の下位検定としての論理的整合性に欠けると言えよう。
また、Kirk (1982, p.371) は、単純主効果の検定は興味深いが2つの処理間の 交互作用を理解するには不十分である、としている。そのためには、彼は、次の節の 処理-対比交互作用(treatment-contrast interactions)や対比-対比交互作用( contrast-contrast interactions)の検定を行うのがよい、と言っている。
Figure 1.3 で見たように、2つの処理間に交互作用がある時には、ある処理の 対比、すなわちある処理の水準間の何らかの平均の差が、もう1つの処理の2つ又は それ以上の水準間で異なる。このような交互作用は、 処理-対比交互作用と 呼ばれ、通常言われる(全体的)交互作用と区別される。
処理-対比交互作用の有無を検討するためには、通常各セルの平均値をプロ ットし、関心ある対比
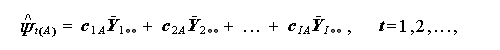
|
(1.89) |
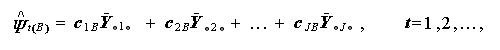
|
(1.90) |
この場合の帰無仮説は、
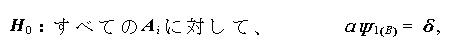
|
(1.91) |
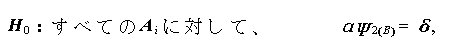
|
(1.92) |

|

|
(1.93) |
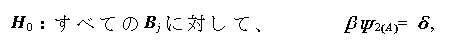
|
(1.94) |

|

|
(1.95) |
任意のBjに対する$\psi_{t(A)}$は、
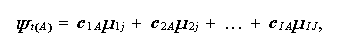
|
(1.96) |
これらの 処理・対比交互作用平方和(treatment-contrast interaction sum of squares)は、

|
(1.97) |

|
(1.98) |
 は、それ
ぞれ、対比$\psi_{t(B)},\psi_{t(A)}$での係数 c の2乗和である。さらに、
(1.97)、(1.98)式の平方和の自由度は、それぞれ、I-1、およびJ-1である。
は、それ
ぞれ、対比$\psi_{t(B)},\psi_{t(A)}$での係数 c の2乗和である。さらに、
(1.97)、(1.98)式の平方和の自由度は、それぞれ、I-1、およびJ-1である。
これらの平均平方を誤差平均平方で割って得られるF比によるF-検定で、 (1.91)式から (1.94)式のようないくつかの帰無仮説が棄却されると、われわれの 次の関心は、 棄却された仮説に対応する対比が、もう一方の処理のどの対比と交互作用を しているかを検討する点に移る。この交互作用は、上述の処理・対比交互作用 に対して、 対比・対比交互作用(contrast-contrast interaction)と呼ば れる。
対比・対比交互作用平方和は、

|
(1.99) |
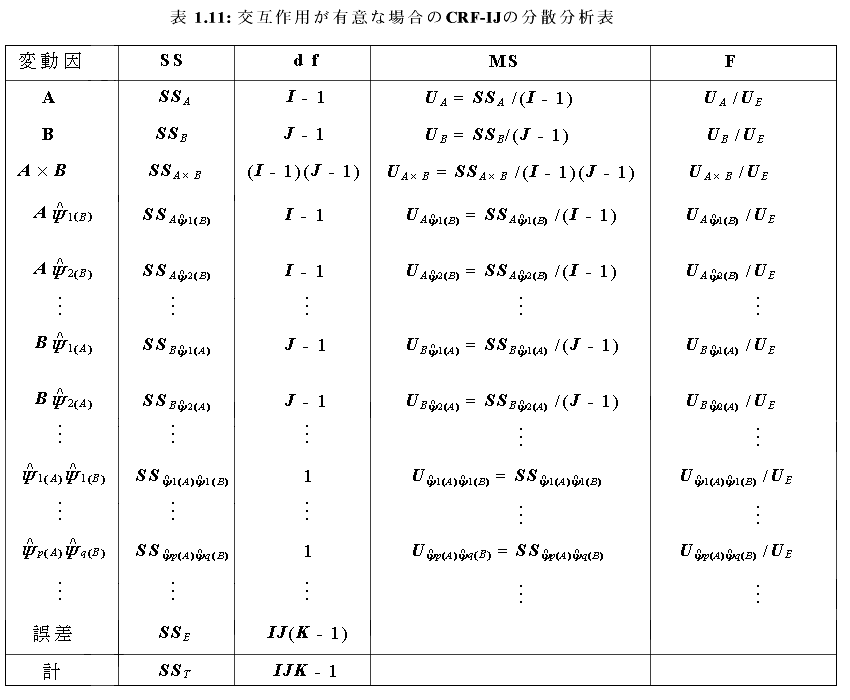
したがって、Table 1.5 で、処理AとBの交互作用が有意な場合の分散分析表は、 Table 1.11 のようになる。
|
脚注1: 3要因デザインでは、 単純交互作 用効果(simple interaction effect)が考えられる。これは、3つの要因の うち1つの要因のある水準を固定した時の2次の交互作用をさす。 戻る
脚注2: 一方、その推定値は、もちろん

Bjでの  である。
戻る
である。
戻る