このページは、令和２年４月２５日に一部更新しました。
1.3 節で述べた CR-p デザインで、主効果が有意の場合、多重比較で実験あたり の危険率のコントロールの問題が存在したように、全体的交互作用が有意の場合、 例えば対比ー対比交互作用の検定に際して、事後検定を行う場合には同様な問題が 生じる。SAS では２要因以上のデザインにおける対比ー対比交互作用の検定には、 contrast 文を用いることにより実行できるが、この方法では危険率のコントロールを 対比ごとにしか行っていないことに注意が必要である。
MANOVA の場合には、例えば O'Brien and Kaiser (1985) が反復測度デザイン の文脈で SPF-pq デザインの対比ー対比交互作用の検定時における実験（族）あたり の危険率のコントロールの問題を論じているが、ANOVA では筆者の知る限りでは 本邦では広津 (1981) ぐらいである。
広津にもあるように、このような場合、族あたりの危険率のコントロールを行う とすれば、Scheff\'e 方式をつぎのように用いればよい。ここで、簡単のため、 CRF-IJ デザインにおける各セルの繰り返し数は等しく K であるとすると、任意の 対比（正確には、対比ー対比交互作用またはそれらの線形結合） を $\hat{\psi}_{t(A,B)}$ と書くとして、
|
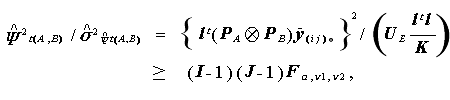
(1.100) |
ここで、$\nu_1=(I-1)(J-1)$ 及び $\nu_2=N-IJ$ である。また、行列 PA
及び PB は、それぞれ処理 A 及び処理 B についての (I -1) 行 I 列
及び (J -1) 行 J 列なる、I 次及び J 次正規直交対比行列の I -1 行、
および J -1 行である。また、$\otimes$ は、 クロネッカー積
(Kronecker product) を表す。また、 
は、
IJ 個の要素的交互作用 $\gamma$ に対応する 
の実現
値 
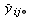を順に並べたものである。また、ベクトル l が
例えば単位ベクトルの場合は、単純な要素的交互作用 $\gamma$ に等しい。
ただし、このようにすると確かに族あたりの危険率はコントロールできるが、 名目危険率 $\alpha$ に対して実質的な危険率は大変小さくなり、その結果検出力 が低くなってしまう危険もある。それを回避するための方法として、広津は幾つかの 方法を述べているが、ここでは省略する。
