前節のプログラムの冒頭のコメントの最後で、SAS を用いて対比ー対比交互作用 の検定を行う場合、SAS の contrast 文の values を指定するには、それぞれの 要因の対比行列のクロネッカー積を計算すればよいことを指摘した。この節では、 クロネッカー積の定義とその具体的な計算方法を示す。
まず最初に、一般のクロネッカー積の定義を述べると、2つの行列 A と B のクロネッカー積は、それらがそれぞれ m 行 n 列、及び p 行 q 列 の行列
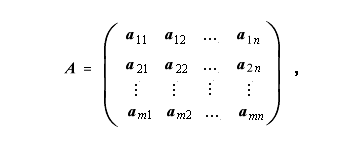
|
(1.101) |
及び
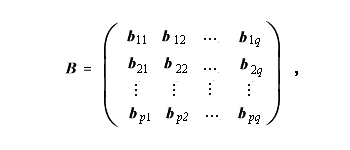
|
(1.102) |
として、
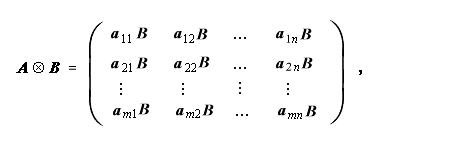
|
(1.103) |
と、定義される。
一般に行列演算では、ある行列に定数を掛けるということは、その行列の すべての要素にその定数を掛けることを意味するので、2つの行列 A と B のクロネッカー積は、mp 行 nq 列の行列になることがわかる。
つぎに、分散分析における対比ー対比交互作用の文脈では、行列 A と B は CRF-IJ デザインでは、2つの要因それぞれの水準間の対比の係数を 行ごとに並べた対比行列 Ca、Cb が対応する。これらの次数は、 理論的な議論を行う場合は通常それぞれ I-1 行 I 列、及び J-1 行 J 列 の行列となるが、SAS の contrast 文で values を指定する場合には、これらの 行数はいくつでもよい。例えば、上述の例ではこれらはつぎのようになる:
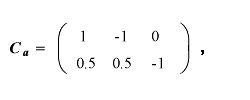
|
(1.104) |
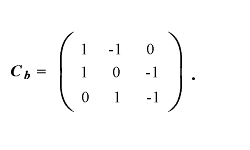
|
(1.105) |
これら2つの行列のクロネッカー積 Ca \otimes Cb が、上述のプログラム の対比ー対比交互作用検討のための contrast 文の6行の values セットになって いることを確かめてみよ。
実は、クロネッカー積は SAS/IML を用いると、つぎのようなプログラムにより簡単 に計算させることができる。
options ps=60 ls=80;
proc iml;
c_a={1 -1 0, 0.5 0.5 -1};
c_b={1 -1 0, 1 0 -1, 0 1 -1};
print "original matrices, c_a, and c_b", c_a c_b;
kron=c_a@c_b;
print "Kronecker product of c_a, and c_b", kron;
quit;
|
うえの例は、2つの要因のそれぞれの水準の2つ、及び3つの対比から6通りの 対比ー対比交互作用の係数を計算させるケースであるが、例えば単一の対比ー対比 交互作用の係数を計算させるためには、Ca、Cb 共に1つの対比を1行に並べ たものを用いて、クロネッカー積を計算すればよい。この場合、結果的には2つの 行列はそれぞれ行ベクトルとみなすことができる。
最後に、3要因以上の交互作用の部分的交互作用を見たいときはどうすればよい であろうか。この場合には、各要因の水準に関する検討したい対比を行に並べた 行列を Ca、Cb、Cc、などとすると、Ca \otimes Cb \otimes Cc \otimes ・・・ なるクロネッカー積を計算すればよい。このような 場合には、SAS/IML による計算が便利である。