乱塊法の構造模型は、まず母数模型の場合、つぎのように表わされる。
|
ここで、$\mu$は一般平均、$\alpha_i$は処理 A の第 i 水準の(主)効果、 $\pi_k$は、局外母数で、区画(block)(したがって、ブロック因子)の第 k 水 準の効果、 Eik は、誤差項である。
$\alpha$、$\pi$、E に関しては、次の仮定をおく:

|
(1.107) |

|
(1.108) |
帰無仮説は、次の2つであるが、主要な関心は、第1の仮説にある。
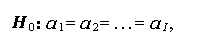
|
(1.109) |

|
(1.110) |
データは、Table 1.12 のようになる。ここで、因子 BL はブロック因子で局外母数 に対応する。

|
この場合の分散分析表は、Table 1.13 のようになる。

|
ここで、

|
(1.111) |

|
(1.112) |
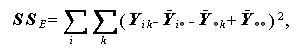
|
(1.113) |

|
(1.114) |

|
(1.115) |
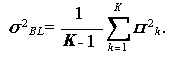
|
(1.116) |
つぎに、乱塊法デザインで通常最もよく用いられる混合模型は、 つぎのようになる:
|
ここで、 Yik は因子 A の水準 i かつブロック因子 BL の第 k 水準における 測定値を実現値(realization)とする確率変数、$\mu$は一般平均で定 数、$\alpha_i$は因子 A の(水準 i の)主効果で定数、 BLk はブロッ ク因子の水準 k の効果に関する確率変数、 Eik は誤差項を表す確率変数 である。
(1.117) 式の模型が混合模型である理由は、誤差項 Eik を除く右辺の項に 定数 $\alpha_i$ と(確率)変数が両方現れるからである。
この場合の分散分析表は、Table 1.13 の母数模型の場合と同じであるが、 母数模型の場合の仮定の1つである (1.107) 式は
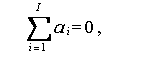
|
(1.118) |

|
(1.119) |
また、母数模型における $\sigma_{BL}^2$ は、このような (1.116) 式による定義では なく、(1.119) 式における正規分布の分散母数となる。
いずれにせよ、 RB-I デザインでは (1.114) 式の全平方和 SST を因子A、 ブロック因子BL、及び誤差の3つの平方和に分解し、Table 1.13 の誤差平方和の不偏 分散(平均平方)を基準にした時、因子Aやブロック因子BLの平方和の不偏分散 が帰無仮説のもとでどれ程大きいかを検討する。