このページは、令和２年４月２５日に一部更新しました。
Table 1.12 のような１要因反復測度デザインは、これまで述べてきた ANOVA によらず、多変量的な取り扱いをすることにより検討することも可能である。この 場合のモデルは、まず
|
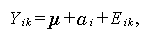
(1.120) |
を仮定する。ここで、(αi, i=1,2,…,I) については、ANOVAにおける (1.117) 式と同じであるが、誤差項 Eik に対する取り扱いが ANOVA の (1.108) 式と異なり、
|
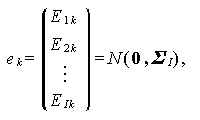
(1.121) |
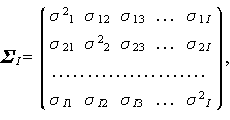
すなわち、誤差ベクトル ek は、平均が 0 で、任意の I 次の共分散行列 $\mbSigma_I$
|
(1.122) |
を持つ 多変量正規分布 (multivariate normal distribution) に従う、 と仮定される。
したがって、多変量正規分布の仮定を除くと、反復測度デザイン の場合のような（複合）対称性や球形仮定などの特別な制約は、一切 水準間に課されないことに注意せよ。
帰無仮説 (1.109) 式の検定には、つぎの
|
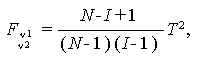
(1.123) |
が、帰無仮説のもとで、自由度
|
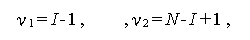
(1.124) |
なる F - 分布に従うことを利用する。ここで、
|
(1.125) |
ここで、\bar{\bf x} は I -1 次ベクトルで、反復測度の例えば隣接２水準における 観測値の平均の差
|
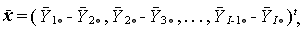
(1.126) |
を要素とするものである。また、Ux は、I -1 次の標本共分散行列で
|
(1.127) |
|
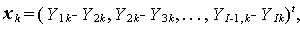
(1.128) |
(1.125) 式の T 2 は、ホテリングの T
2- 統計量とか（Morrison, 1967)、一般化 T 2-
統計量 (generalized T 2 -statistic) (Anderson, 1958,
1984) と呼ばれる統計量を、(1.128) 式のような変量の場合に適用したも
ので、一般的には、p 次元ベクトル x 1,...,
x N が多変量正規分布
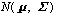からの無作為標本だとするとき、帰無仮説
|
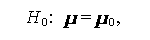
(1.129) |
のもとで尤度比基準
|
(1.130) |
により統計量を求めるとき、λ の右辺の一部に
|
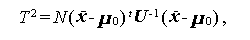
(1.131) |
(1.131) 式の T 2 の分布は、付録Ｂに示す Bowker (1960) の定理を用いて、 帰無仮説のもとでは、
|
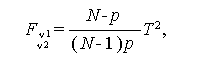
(1.132) |
が、自由度
|
(1.133) |
さて、(1.126) 式の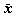 
は、たまたま (1.128) 式で与えられる
隣接２水準間の観測値の差となっているが、一般的には任意の対比行列 C、
及び第 k 観測単位（被験者）の観測値ベクトル
|
(1.134) |
を用いて
|
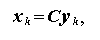
(1.135) |
とできる。ここで、C は I-1 行 I 列のパターン行列である。一方、 x k は I -1 次ベクトルになることに注意せよ。
(1.135) 式を用いると、(1.125) 式の T 2 は、
|
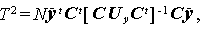
(1.136) |
と書ける。ここで、
|
(1.137) |
このように、Hotelling の T 2-統計量は 尤度比統計量(likelihood ratio statistic) として導かれるが、 結び-交わりの原理 (union-intersection principle)から 導くこともできる (Morrison, 1967)。この原理からは、たとえば (1.125) 式 の T 2 は、行列
|
(1.138) |
の最大固有根（かつ唯一の固有根）として与えられる。同様にして (1.136) 式の T 2は、行列
|
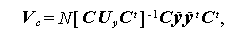
(1.139) |
いずれにせよ、結局のところホテリングの T 2 統計量を用いた１要因反復 測度デザインデータにおける主効果に関する帰無仮説 (1.109) 式は、((1.123) 式 及び (1.136) 式から明らかなように、つぎの場合に棄却すればよいことがわかる：
|
ここで、F(α,I -1,N - I +1) は、自由度 ν1=I-1 及び ν2=N-I+1 なる F-分布の 右側 100α パーセント棄却点の値である。
さらに、もし主効果の帰無仮説が棄却された場合には、族あたりの危険率を最大 で 100α パーセントに押さえた同時検定をつぎのように行うことができる。 すなわち、(1.135) 式における行列 C の任意の行を列にしたベクト ル c を用いて、任意の対比を
|
(1.141) |
として、如何なる対比についての帰無仮説 H 0: ψ=0 も、つぎ の場合に棄却すればよい：
|
