このページは、令和２年４月２５日に一部更新しました。
1.5.3 節で１要因反復測度デザインの F-比の歪みの問題を回避する方法として、 ホテリングの T 2 統計量を用いた分析を紹介した。この節では、２要因の場合に 同様な問題を回避できる方法を紹介する。そのためには、GMANOVA を２要因反復測度 デザインデータの分析に応用すればよい。GMANOVA に関しては、詳しくは第３章で ふれることにして、この節ではこれをどのように２要因反復測度デザインの場合に 応用するのかについてふれる。実は、1.5.3 節でのホテリングの T 2 統計量 を用いた分析は、ここで述べる方法の特殊ケースなのである。
GMANOVA では、一般に ANOVA と異なり各被験者のデータは t 変量の測定値 から成り、サンプルサイズを N として、つぎのような行列で表される：
|
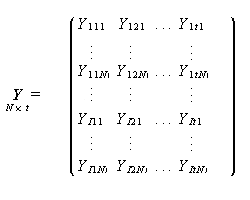
(1.182) |
さらに、このデータ行列 Y に対して、つぎのようなモデルを考える (Potthoff & Roy, 1964)：
|
(1.183) |
ここで、A は、N 行 q 列の既知の デザイン行列 (design matrix) 、Θ は q 行 p 列の未知の 母数行列、B は p 行 t 列の既知の変換行列、E は N 行 t 列 の誤差行列である。
GMANOVA における仮説は、うえの未知パラメータ Θ に対する 多変量一般線形仮説 (multivariate general linear hypothesis) すなわち、
|
と表される。この
である。ここで、一般に C は g 行 q 列の行列で、仮説行
列 (hypothesis matrix) と呼ばれ、一般線形モデルの q 個の母数に関す
る g 個の仮説（対比）に対応する。また rankC=g\le r であり、C は
である。ここで、r は、Θ の行の r と q-r への分割に対応する
値であり、行列 A の分割、
にも対応する。ここで、rank A=r である。
行列 A や C の分割は、GMANOVA モデルの未知母数の 再パラメータ
化 (reparametrization) に関係する。この詳細は、第３章を参照のこと。
一方、 M は p 行 u 列の行列で、
ここで、例えば通常の MANOVA の帰無仮説はうえの (1.184) 式で
M=I、t=p の場合で、この場合帰無仮説は
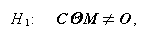
(1.185)
(1.186)
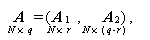
(1.187)
である。
(1.188)
|
または、再パラメータ化した場合、
|
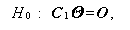
(1.190) |
とすることに等しい。
これに対して、１要因以上の反復測度ばかりのデザインの場合は、GMANOVA の 行列 C がスカラー量の 1 であるケースにあたり、帰無仮説は
|
となる。
いずれにせよ、GMANOVA での主効果の検定は、次式で定義される行列
|
|
|
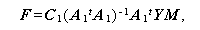
に対して、行列 H (H+E) -1 の固有根のうち最大根の、(1.184) 式 の帰無仮説のもとでの分布の上側 100α パーセント点のグラフが、 Heck (1960)、Foster (1957a,b)、Foster and Rees (1957)、Pillai (1960, 1964, 1965) により与えられていることを利用するのが、最も一般的なやり方である。これらの うち、Heck chart が最もよく知られている。
ここで、通常、Roy の最大根基準 (Roy, 1945) と呼ばれる MANOVA (GMANOVA)
検定量は、 Morrison (1967) も指摘しているように Heck chart に
おける最大根そのものとはと異なり、行列 H,E -1 の固有根のうちの
最大根であるので、注意が必要である。Roy の最大根を c 1 と書くと、
Heck chart における最大根 θ1 は、上の２つの固有値問題の形
から、
となる。
しかし、一般に (G)MANOVA における主効果や全 体的交互作用（平行性仮説）についての帰無仮説の検定における基準は、Roy の最 大特性根基準と呼ばれる上記の基準の他にも、 Wilks のラムダ基準 (Wilks, 1932)、 Lawley-Hotelling の跡基準 (Lawley, 1938; Hotelling, 1947, 1951)、 Bartlett-Pillai の跡基準 (Bartlett, 1939; Nanda, 1950; Pillai, 1955)、が 知られており、SAS や SPSS では、これらの近似分布等をすべて出力するので、 少なくとも主効果や平行性仮説の検定には Heck chart 等は不要である。
例えば、Wilks のラムダ基準では、
|
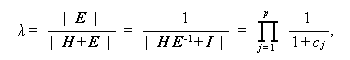
(1.194) |
として、帰無仮説のもとで、漸近的に尤度比統計量
|
(1.195) |
が自由度
|
(1.196) |
の χ2- 分布に従うことを用いる。ここで、u は行列 M の階数である。 既に述べたように、１要因ＭＡＮＯＶＡでは、g=I-1、r=I、u=p となる。 また、(1.194) 式の c j は、行列 H E-1 の j 番目の固有根である。
もし、s=min(g,u)=1, 2 の場合には、正確な検定量が知られている (Wilks, 1935)。まず、s =1 の時には、帰無仮説のもとで、
|
(1.197) |
は、自由度 ν1=2m+2,ν2=2n+2 の F - 分布に従う。さらに、この時に
かぎり (1.194) 式から、Roy の最大根を c 1 とすると、
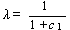が成り立つので、
|
(1.198) |
s =2 の時には
|
(1.199) |
が、自由度 ν1=4m+6,ν2=4n+4 の F - 分布に従う。ここで、 m=(| g-u |-1)/2、n=(N-r-u -1)/2 である。
これに対して、水準数が小さいときは、次の F - 近似の方がより正確である (Anderson, 1984)：
|
(1.200) |
ここで、この F の自由度は
|
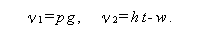
(1.201) |
また、h 、t 、w は、
|
(1.202) |
他の基準の場合の近似統計量については、第３章を参照のこと。
ところで、これらの基準のうち、Roy の最大特性根基準については、SAS と SPSS とでは 出力結果が異なるので注意を要する。SAS の場合は、 Roy の最大根そのものが出力されるが、SPSS では Roy の最大根の項に上記 の θ1 すなわち Heck chart 用に変換された値が出力される。
最後に、(1.184) 式で表される何らかの主効果もしくは全体的交互作用について の帰無仮説が棄却された場合の対比もしくは部分的交互作用の検定について 述べる。既に述べたように、 SAS や SPSS ではこのような場合、対比検定の 族あたりの危険率は全くコントロール されないので、事後的非直交対比を考えている場合には、厳密には 特別の手当が必要である。これを行うには、つぎの Roy (1957) 及 び Roy and Bose (1953) による同時検定を利用すればよい。
Roy 及び Bose によれば、多変量一般線形モデルのすべての関数
|
(1.203) |
についての 100(1-α) パーセントの同時信頼区間は、
|
(1.204) |
で与えられる。ここで、xα\equiv xα(s ,m ,n ) は、Heck chart から得られる 100α パーセント点の値である。ここで、一般に Heck chart における xα,(s ,m ,n ) のパラメータは、一般線形仮説 (1.184) 式の検定 において、それぞれ s=min(g,u)、u=rank M、m=(| g-u|-1)/2、 n=(N-r-u-1)/2 である。
また、a は u 次 の非ゼロベクトル、b は q 次のベクトルで、つぎのように長さを 選ぶものとする：
|
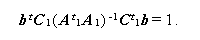
(1.205) |
言い換えれば、対比帰無仮説、
|
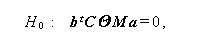
(1.206) |
の検定には、有意水準 α の棄却点を、
|
とすればよい。ここで、要因に関する SSCP 行列を H、誤差 SSCP 行列を
E として、H E -1 の最大固有根すなわち Roy の最大根を
c 1 と書くと、Heck chart は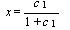 
についての分布の
表であるので、(1.207) 式の右辺の値 xα は、c1(α) すなわ
ち Roy の最大根
の分布の有意水準 α の棄却点の値にあたることに注意が必要である。
