このページは、令和２年４月２５日に一部更新しました。

１.６.５節　 ２要因反復測度デザイン分析におけるクロネッカー積の利用方法

　 1.4.7 節で、完全無作為化２要因デザインの部分交互作用の検定にクロネッカー 積が重要な役割を果たすことを学んだが、反復測度乱塊２要因デザインデータの GMANOVA 分析においてもクロネッカー積が重要な役割を果たす。

　 というのは、1.6.3 節で説明したように、反復測度ばかりの ANOVA データは、 GMANOVA の特殊ケースにあたり、主効果の帰無仮説は (1.191) 式で表すことが できることを思い出そう。この行列 M の各列は一般的に、p 個の反復 測度を線形変換するための t 個の係数（列）ベクトルなのであり、一種の 対比を構成する。独立測度の対比（行）ベクトルが (1.184) 式の一般線形仮説 の行列 C の各行を構成するのに対して、反復測度の対比を列ベクトルの 形で構成するのが行列 M なのである。

　 例えば、1.5.5 節の１要因反復測度 RB-p デザインデータの manova 文による 分析プログラムの m= の項に指定した行列は、まさにこの (1.191) 式の M 行列に他ならない。ただし、SAS では m= の項に、この M 行列そのものではなく、その行と列を転置したものを指定する 約束になっているので、注意せよ。

　 さて、この M 行列は２要因以上の場合どう定義できるのであろうか。実は、 このような場合、各々の要因の反復測度間対比行列を M _A、M _B、 M _C 等とすると、

(1.208)

　 さて、1.6.3 節で紹介したように、一般に GMANOVA の多変量一般線形仮説 (1.184) 式の検定は、(1.192) 式及び (1.193) 式より計算される２つの行列を 用いて定義される新たな行列の固有根の分布を利用して検定するわけであるが、 そこでも指摘したように、一般的には正確な分布の形は分かっておらず、Heck チャート等の表を用いなければならない。また、その時のパラメータは、Heck チャートの場合、線形仮説を構成する行列 C、Θ、及び M の 次数の情報を用いて、

(1.209)

と表せる。

　 しかも、やはり 1.6.3 節で指摘したように、s =1 の場合には、線形仮説の もとでは例えば Wilks の λ もしくは Roy の最大根 c ₁ を用いると、 (1.197) 式や (1.198) 式の右辺は正確な F-分布に従うことが分かっている。

　 実は、反復測度ばかりの ANOVA デザインデータの場合、これらの結果を用いると、 (1.209) 式の s =1 であることは明白である。なぜならば、このようなデザインでは、

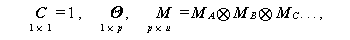
(1.210)

であり、さらに A ₁= 1_N =(1, 1, ... , 1)^t であるので、Heck チ ャートの３つのパラメータの値は、

(1.211)

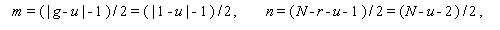
(1.212)

が成り立つ。したがって、まず s =1 より、主効果検定のための固有根の正確な 分布がわかっており、F-分布となる。

　 また、このようなデータの場合、(1.192) 式の H と (1.193) 式の E は、簡単になり、

(1.213)

と書けることも明らかである。ここで、 は、p 個の変量 それぞれの平均値を要素とする列ベクトルである。したがって、主効果の検定には うえの H と E より tr(H, E ^-1) を計算し、得られた Roy の最大根 c ₁ より (1.198) 式を用いて

(1.214)

　 最後に、一般線形仮説の主効果や全体的交互作用が棄却された場合の、Roy-Bose 方式による対比等の同時検定についても、つぎのように (1.207) 式の左辺は簡略化 できる。すなわち、まず (1.205) 式は反復測度ばかりのデザインでは、簡単になり 結局　 とすればよいことが分かる。

　 また、(1.207) 式の左辺もこの時

(1.215)

	(1.216)

の時対比帰無仮説 (1.206) 式を棄却すればよい。ここで、列ベクトル a は、 通常単位ベクトル e ₁=(1, 0, 0, ... , 0)^t、 e ₂=(0, 1, 0, ... , 0)^t、などを指定すれば よく、これらは順に M 行列の１番目、２番目等の対比列ベクトルを指定する ことに等しい。