このページは、平成2年年4月27日に一部更新しました。
![]()
教育や心理の分野では、多くの 場合分割区画デザインは原型としてのそれではなく、第1局外因子は単に第2 局外因子の集合、言い換えれば大ブロックでしかなく、さらに第2局外因子の各 水準を各被験者(1人)とみなす反復測度デザインを指すことが多い。
このような、反復測度 SPF-p.q デザインでは、大ブロックの p 水準を無作為に 割り付けられる主要因子 A は独立測度要因(被験者間要因)となり、一人の被 験者がすべて反応させられる同因子 B は反復測度要因(被験者内要因)とな る。
したがって、反復測度 RB-p デザインや同 RBF-p.q デザインの場合と同様、 反復測度間の相関構造如何によっては、F-比の歪みを生ずるので、球形仮定の 検討が必要となる。ただし、反復測度 SPF-p.q デザインでは新たに独立測度要因が 加わるので、球形検定は反復測度 RB-p デザインや同 RBF-p.q デザインの場合 ほど単純ではなくなり、1.7 節の最初に紹介したような多標本球形仮定の検討が 必要になる。
多標本球形仮定の概念が教育や心理の分野の文献に現れたのは、70 年代から 80 年代にかけてである。すなわち、Huynh and Feldt (1970) は、表 1.20 の SPF-I.J デザインにおける処理B(反復測度要因)及び A\times B について の F 比が正確な F -分布に従うための条件は、

|
(1.220) |
であり、この仮説は、

|
(1.221) |
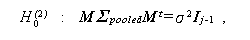
|
(1.222) |
の2つのステップで検定できることを示した。
ここで、M は J -1行 J 列の正規直交対比行列、{Σi , i =1,2, ... ,I } は J 行 J 列の母共分散行列、IJ-1 は J -1 次の 単位行列である。また、Σpooled は、
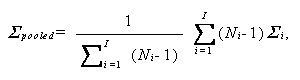
|
(1.223) |
(1.220) 式は、多標本球形仮定とか (Harris, 1984; Mendoza, 1980)、 多標本循環性仮定(multisample circularity assumption) と呼ばれたりする (Mendoza, 1980; Kirk, 1982)。
計量心理学の分野では、最初 Mendoza (1980) が、(1.220) 式の多標本球形仮説ではなく、もとの反復測定変数間の共分散行列に関する帰無仮説
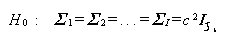
|
(1.224) |
この場合、多標本球形仮説の第1ステップは、

|
(1.225) |
ここで、(1.224) 式の多標本球形仮説は、(1.220) 式の多標本球形仮説が成り立つための十分条件ではあるが、必ずしも必要条件ではないことに注意が必要である。(1.224) 式の分散分析の文脈での多標本球形仮説の検定は、その後、Harris (1984) が提案している。
この場合、第一ステップの I 個の共分散行列の等質性の検定 (test for homogeneity of covariance matrices) には、既に 1.3.6 節の SAS プログラムで用いた discrim プロシジャにオプションとして用意されてい る Box (1949) の方法を使えばよい (Huynh and Feldt, 1970; Kirk, 1982)。 Kirk (1982) によれば、この検定は Bartlett の分散の等質性の検定の拡張であ り、非正規性に対しては頑健でないという。
これに対して、第2ステップの (1.222) 式の検定には、Mauchly の球形 検定がそのまま使える。もちろん、この場合球形仮定が棄却されたとすると、 表 1.20 の処理 B 及び A \times B の効果の検定時の F - 分布の自由度は、Box の ε 因子 (G-G Epsilon 又は H-F Epsilon) によって調整したものを用いる。一方、処理 A の方は独立測度要因なので、F-比はゆがまない。
いずれにせよ、多標本球形仮定を2ステップで検定する方法は、 2ステップ多標本球形検定 (a two-step multisample sphericity test) と呼ぶことができる。一方、Mendoza (1980) は、多標本球形仮定が1ステップで検定できることを示した。この方法は、1ステップ多標本球形検定 (a single-step multisample sphericity test) と言える。
ところで、Mendoza (1980) の多標本球形検定は、実はその12年 前に数理統計学の分野の論文に、Sugiura and Nagao (1968) がそれを含むより 一般的な形で提案しているのである。明らかに Mendoza は、Sugiura らの論文を 見落していたことになる。研究者の世界では、本来あってはならないことであるが、 時々このようなことが起こり得るのである。
ところで、共分散行列の等質性の検定について注意すべきことは、多標本 球形検定の文脈では2ステップ多標本球形検定の第1ステップとしての同等質性 の検定は、もとの反復測度変数に対してではなく正規直交化された 変数に対して行わねばならない点である。
この点に関して、SPSS は現状の最新バージョン 12.0 でも、残念ながら、もとの反復測度変数に関する共分散行列の等質性の検定、すなわち (1.225) 式の帰無仮説に対する Box の共分散行列の等質性検定を F-検定により行なっているに過ぎない。先ほどの多標本球形仮説 (1.220) と(1.224) との関係と同様、この (1.225) 式の帰無仮説は (1.221) 式が成り立つための十分条件ではあるが、必ずしも必要条件ではないので、不十分である。この点に関しては、筆者の方から最近(平成16年2月)SPSS に対して改善を要望したので、早晩正確な多標本球形仮説の検定が SPSS でもできるようになると思われる。
一方、SAS の場合、既にふれたように、anova や glm プロシジャ(の repeated 文)には多標本球形仮説の第2ステップしか現状では(バージョン 8.2)出力しない。repeated 文には共分散行列の等質性の検定のオプションがないので、discrim プロシジャを用いる必要がある。そして、このプロシジャで pool=text なるオプションを選択すると、Box の共分散行列の等質性の検定(ただし、SAS では SPSS と異なり、χ2-検定)を行ってくれる。ただし、多標本球形検定の文脈では、これを実行する前にあらかじめ data ステップを組み、正規直交変数を作成しておく必要がある。この点に関しては、SPSS と同様、筆者の方から最近(平成16年2月)SAS に対して改善を要望したので、早晩正確な多標本球形仮説の検定が SAS でもできるようになると思われる。
最後に、任意の(反復測度)変数について簡単に正規直交変数化する方法を 紹介する。それは、つぎのその係数の一部を示した ヘルメルト対比 (Helmert contrast) を作成するものである。

|
ここで、例えば3変数の Helmert 対比行列は、
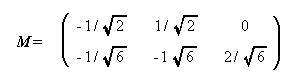
|
と書ける。また、対比の係数の分母の値は、Table 1.22 の例えば第1行目に
ついては、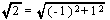 、
、
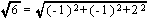 の
ように計算すればよい。
の
ように計算すればよい。
多標本球形仮説の詳細については、第2章を参照のこと。