このページは、令和2年4月27日に一部更新しました。
![]()
| 反復測度 SPF-p.q デザインの GMANOVA 分析用 プログラムの例 |
この節では、SAS/IML による反復測度 SPF-p.q デザインの GMANOVA 分析の ためのプログラム例を示す。データは、前節で引用した O'Brien らの反復測度 SPF-3.3 デザインデータを用いる。
前節でもふれたように、彼らのデータは非釣り合い型デザインなので、SAS の 4つの平方和のうちの Type III よりも Type II の方がよいと考えられるが、前節 と同様にここでも Type III 平方和による方式で実行する場合の例を示す。
以下の IML プログラムからわかるように、実は通常の GMANOVA で主効果なり 同時検定に際して用いられる (1.192) 式や (1.207) 式で定義されている行列 F の内容を検討すると、反復測度の主効果を見るための (1.192) 式の F の右辺のうち、(A1t ,A1))-1 及び A1t,Y は、SPF-I.J デザインでは、A1 が、
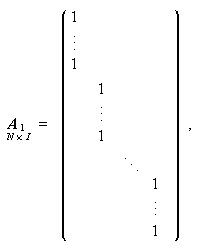
|
(1.240) |

|
(1.241) |

|
(1.242) |
となる。ここで、(1.242) 式の要素  は、第 i 独立測度
グループで第 j 反復測度変数のデータの和である。したがって、(1.193)
式の右辺の行列 C1 がこの場合、
は、第 i 独立測度
グループで第 j 反復測度変数のデータの和である。したがって、(1.193)
式の右辺の行列 C1 がこの場合、

|
(1.243) |
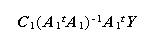
|
の第 j 列は、反復測度第 j 変数のグループごとの(単純)平均 の和になっていることがわかる。
つまり、通常の GMANOVA では、このような独立測度の水準をつぶす場合、水 準(グループ)ごとの単純平均の和を作っていることになり、水準間でサンプル数 が異なる、すなわち非釣り合い型デザインデータの場合、場合によっては都合が 悪い。これを避けるには、(1.241) 式の対角要素の値をすべて I/N にすればよい。 この操作は、独立測度の水準をつぶす場合、結局単純平均の和を作るのではなく、 各水準(グループ)のサンプル数による加重平均を考え ることに等しい。
前者と後者の平均の作り方は、SAS/STAT では平方和としてそれぞれ、Type III を 選択するか Type II を選択するかと対応している。
このようなわけで、つぎの SAS/IML プログラムでは、ユーザがこれらのうちの どちらを選択するかをユーザ自身で指定できるようにしてある(指定すべき9つの パラメータ項のうち、(d) の項)。
また、ユーザは最初、Heck チャートの3つのパラメータの値が分からないものと して、それらを打ち出すために、(i) の項の heck_c の値をゼロと指定して実行 しなければならない。これを実行し、3つのパラメータの値から Heck チャートを 見て、棄却点の値を図から読みとり、2回目のプログラム実行時には heck_c の 値をゼロから変更する必要がある。
つぎのプログラムは、(i) の項を見れば分かるように、2回目の実行時のための ものである。
*----------------------------------------------------------------------* | December 1, 1998 | | sas program--imlspfok.sas | | | | SAS/IML program for executing simultaneous contrast tests using a | | Roy-Bose simultaneous test procedure for an arbitrary repeated | | measures SPF.p-q design data. | | | | Data is Table 3, of O'Brien & Keiser (1985). | |
| Caution! |
| |
| (1) Users must revise the necessary parts of the following program |
| in order to specify (a) raw data, (b) variable names for repeated |
| measures, (c) levels of between-subjects factor A of all samples, |
| (d) type of sum of squares, (e) contrast matrix for a between- |
| subjects factor A, (f) names of contrasts for the between-subjecs |
| factor A, (g) transformation matrix for a within-subjects factor P, |
| (h) names of contrasts for within-subjects factor P, and (i) Heck |
| critical value, which are suggested by the comments which begin |
| with '/* Specify ... '. |
| (2) Users must execute this program twice. In the first execution, |
| set the heck_c value for testing the overall interaction equals to |
| zero. In the second execution, specify it according to the param- |
| eters s_heck, m_heck, and n_heck, looking at the Heck chart. |
| (3) It should be noticed that there is no need to specify heck_c |
| values for testing the two main effects. For, test statistics be- |
| come exact in these cases. |
| (4) Types of sum of squares (denoted by 'typess' below) must be 2 or |
| 3, which correspond to Type II SS and Type III SS in SAS anova and |
| glm procedures, respectively. |
| |
*----------------------------------------------------------------------*;
options pagesize=60 ls=80;
/* (1) data input */
data work;
/* (a) Specify variable names and their labels */
input ssno 2. +1 group 1. +1 (pretest posttest followup) (1.);
label ssno='sample number'
group='group number to which subject belongs'
pretest='mark on a pretest'
posttest='mark on a posttest'
followup='mark on a follow-up test';
cards;
1 1 233
2 1 434
3 1 657
4 1 534
5 1 464
6 2 899
7 2 589
8 2 356
9 2 445
10 3 478
11 3 356
12 3 698
13 3 668
14 3 256
15 3 377
16 3 578
;
|
proc iml;
use work;
/* (b) Specify the variable names for repeated measures, which must
be the same as those defined by the input statement */
read all var{pretest posttest followup}
into y;
print "Input raw-data matrix, Y", y;
yrow=nrow(y); ycol=ncol(y);
if yrow < ycol then do;
print "number of samples is too small"; return;
end;
/* (c) Specify the levels of the factor A of each sample */
level={1,1,1,1,1,2,2,2,2,3,3,3,3,3,3,3};
/* (d) Specify the type of sum of squares:
(1) typess=2.....weighted average case (Type II SS in SAS glm)
(2) typess=3.....simple average case (Type III SS in SAS glm) */
typess=3;
a_1=design(level); /* design matrix A_1 is generated */
ata=a_1`*a_1; /* A_1'A_1 of the design matrix A_1 */
atai=inv(ata);
/* (e) Specify the contrast matrix C for a between-subjects factor A */
c_a={-2 1 1,
0 -1 1};
/* (f) Specify the names of contrasts for the between-subjects effect */
name_ca={c1 c2};
/* (g) Specify the transformation matrix M */
m_p={-1 -1,
1 0,
0 1};
/* (h) Specify the names of contrasts of P effect */
name_mp={m1 m2};
print "design, contrast, and transformation matrices",
a_1, c_a, m_p;
start test(y,yrow,a_1,c,m,atai,p,theta_h,heck_c,typess,
namebet,namewit,namef,namedf1,namedf2,namep,namet);
/* (1) test for overall effect */
crow=nrow(c); ccol=ncol(c);
mrow=nrow(m); mcol=ncol(m);
camul=c*atai;
if typess=2 then camul=shape(1,1,ccol)*ccol/yrow;
f=camul*a_1`*y*m;
contm=camul*c`;
contmi=inv(contm);
h=f`*contmi*f; /* H matrix */
atym=a_1`*y*m;
e=m`*y`*y*m-atym`*atai*atym; /* E matrix */
print h, e;
|
call geneig(eigval,eigvec,h,e); /* generalized eigenproblem */
roy1=eigval[1]; /* Roy's greatest root */
s_heck=crow> |
end;
end;
finish;
namef={F_value}; namep={Prob_ge_F}; namedf1={df_1}; namedf2={df_2};
namet={theta_Heck};
print "*** 1. test for the hypothesis of no interaction effect ***";
c=c_a; /* contrast matrix C for between-subjects levels */
m=m_p; /* transformation matrix M for within-subjects measures */
namebet=name_ca;
namewit=name_mp;
/* (i) Specify the non-zero Heck critical value for the overall
interaction if s_Heck is greater than 1 in the first execution
of this program */
heck_c=0.498;
run test(y,yrow,a_1,c,m,atai,p,theta_h,heck_c,3,
namebet,namewit,namef,namedf1,namedf2,namep,namet);
print "*** 2. test for the hypothesis of no A effect ***";
c=c_a; /* contrast matrix C for between-subjects levels */
mprow=nrow(m_p);
m=shape(1,mprow,1); /* M matrix for testing A effect */
namebet=name_ca;
namewit={m_mean};
run test(y,yrow,a_1,c,m,atai,p,theta_h,heck_c,3,
namebet,namewit,namef,namedf1,namedf2,namep,namet);
print "*** 3. test for the hypothesis of no P effect ***";
cacol=ncol(c_a);
c=shape(1,1,cacol); /* contrast matrix C for between-subjects levels */
m=m_p; /* transformation matrix M for within-subjects measures */
namebet={c_mean};
namewit=name_mp;
run test(y,yrow,a_1,c,m,atai,p,theta_h,heck_c,typess,
namebet,namewit,namef,namedf1,namedf2,namep,namet);
quit;
|
| imlspfok.sas |