このページは、令和2年4月27日に一部更新しました。
![]()
Mauchly (1940) の球形検定は、前節でも指摘したように、もともと 分散分析の文脈から離れて、多変量仮説の検定の一つとして開発されたものであり、 (2.3) 式の球形仮説のもとで、つぎの χ2 の値

|
(2.12) |
が漸近的に自由度
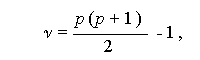
|
(2.13) |
の χ2- 分布に従うことを利用する。ここで、$\hat{\mbSigma}$ は、 母共分散行列 $\mbSigma$ の推定値であり、p 行 p 列から成る。
この検定は、Mauchly により尤度比基準 (likelihood ratio criterion) を用いて導かれたものである。もちろん、この場合の 尤度比 (likelihood ratio)

|
(2.14) |
の分子 L(\omega) は、(2.9) 式の帰無仮説のもとで、N(\mbmu,\;\mbSigma) からの無作為標本 x 1,x 2,...,x N が得られる 条件付き最大尤度 (conditional maximum likelihood) であり、分母 L(\Omega) は、同じく N(\mbmu,\;\mbSigma) からの無作為標本が 得られる無条件最大尤度 (unconditional maximum likelihood) である。
これを分散分析における反復測度デザインの場合に利用するには、(2.5) 式の p 行 p 列の行列 $\hat{\mbSigma}$ のかわりに、(2.5) 式の m 行 m 列の行列 $\mbM \mbSigma \mbM^t$ の $\mbSigma$ を $\hat{\mbSigma}$ で置き換えたものを 用い、

|
(2.15) |
とする。最も単純な1要因反復測度デザインの場合、水準数を1.1.2で用いた I とすれば、$\hat{\mbSigma}$の次数は I 、M はI -1行 I 列、 $\mbM \hat{\mbSigma} \mbM^t$ は、I -1 次、m は I -1 としなければならない。
ただし、現在は(2.12)式の形は使われず、Box (1949) の研究に基づき 修正されたつぎの χ2 を利用する (Huynh & Feldt, 1970):

|
(2.16) |
ここで、

|
(2.17) |
もちろん、上述の1要因反復測度デザインの場合、(2.16) 式の$\hat{\mbSigma}$は $\mbM \hat{\mbSigma} \mbM^t$に、p は I -1に変えなければならない。この時、
ここで、
|
もしうえの帰無仮説が棄却されるならば、処理要因 の効果の有無を検定するためのF比の2つの自由度は共に過大評価されるので、Box の $\epsilon$ 因子を用いて修正することが望ましい。これに関しては現在、 Greenhouse and Geisser (1959) による Greenhouse-Geisser Epsilon (略 して G-G Epsilon) 及び Huynh and Feldt (1976) による Huynh-Feldt Epsilon(略して H-F Epsilon)が使われることが多い。
Huynh と Feldt は、G-G Epsilon がサンプルサイズが小さい時過小評価され、 その結果としてF-検定が過度に保守的 (too conservative) になることを示し、それ に変る指標を開発した。
Box の $\epsilon$ の下限値は、Box (1954b) や Greenhouse and Geisser (1958) も示しているように、1/(I -1)であり、

|
(2.20) |
であり、$\mbSigma$が球形の場合、ε= 1 となる。ただし、H-F Epsilon は、 場合によっては1 以上になり、その時はこれを1とみなす必要がある。
最後に、球形検定に際しての注意事項をあげておく。まず第一に、
| 分散分析の文脈での球形仮説は、あくまでも直交正規化された変数に関するもので ある。 |
すなわち、(2.5) 式の球形仮説は MM t= I m に注意すると、形式的 には (2.9) 式の形と同等、つまりもとの反復測度間の共分散行列が単位行列に等し いということになるが、検定に際してはあくまでももとの変数ではなく直交正規化 された変数に対して行われるべきであり、その意味するところは上のとうりである。 つぎに、
| Mauchly の球形検定を行うためには、最低、水準数 I-1 以上のサンプル数が 必要である。 |
なぜならば、もしそうでないと (2.18) 式の右辺の $\mbM\,\hat{\mbSigma}\,\mbM^t$ の行列式の値がゼロとなり、χν*2 値が計算できないか らである。
この点に関して、実験領域の論文の中には時々水準数よりかなり少ないサン プル数しかデータを取っていないものを見掛けるが、これでは Mauchly の球形 検定を行うことができないわけであり、この型の分散分析を数理統計学的にきち んと行うための必要条件を満たしていないことに注意すべきである。
この問題は、次節で述べる2要因反復測度デザインでは、さらに深刻である。 というのは、この場合、2要因の水準のすべての組み合わせの数(正確には、 組み合わせの総数マイナス1)を下廻るサンプル数では、主効果や交互作用 をみるための F -比の分母に取るべき誤差項の正しい選択のための検定(次節 で述べる大局的球形仮説の検定)が行えないからである。