このページは、令和2年427日に一部更新しました。
![]()
前節の議論では、暗黙のうちに1要因反復測度が仮定されていた。しかし、2要因 反復測度デザインになると、球形仮定の検討は1要因反復測度デザインのように簡単 ではない。
2要因反復測度デザインでは、正確には2種類の球形仮定を検討しなければ ならない(例えば、Kirk, 1982)。1つは大局的球形仮定 (global sphericity assumption) であり、他方は 局所的球形仮定 (local sphericity assumption) である (Crowder & Hand, 1990)。これらは、それぞれ全体的循環性 (overall circularity)、局所的循環性 (local circularity) と呼ばれることもある (Kirk, 1982; Mendoza, Toothaker, & Crain, 1976)。
まず、大局的球形仮定の検定は、大局的帰無仮説

|
(2.21) |
が与えられた時、大局的球形仮説

|
(2.22) |
が成り立つかどうかの検定である。ここで、M は、IJ-1 行 IJ 列の 正規直交対比行列で、$\mbSigma$は、1.6.6 節のデータのように2つの反復測度 要因のすべて の可能な組み合わせ IJ だけの次数を持つ IJ 水準間での母共分散行列、 I IJ-1 は、IJ -1 次の単位行列である。また、(2.21) 式の μij・, : i=1,2, … ,I; : j=1,2, … ,J は、(1.143) 式や (1.163) 式のような通常の分散分析モデルでの母数ではなく、 いわゆるセル平均モデル (cell means model) における処理Aの第 i 水準かつ処理 Bの第 j 水準のセル平均の母数である (Searle, 1987)。
この場合、Mauchly の球形検定は、(2.18) 式および (2.19) 式の I の かわりに IJ とし、M や$\hat{\mbSigma}$ は (2.22) 式のそれらにしな ければならない。
さて、 (2.18) 式の大局的球形仮説が採択されるならば、 大局的球形仮定が成り立っているとみなし、表 1.15 の加算的モデルによる 分散分析を行う。この場合、F比は正確な F-分布に従うので、Box の εεε 因子による調整は通常不要である。
大局的球形仮定が成り立っている時、加算的モデルにより分析を行えばよい 理由は、つぎの通りである:
この場合、どんな対比を選んでも、その交互作用分散はすべて等しくなければ ならない (Rouanet and L\'epine, 1970, pp.155-156)。このことを表 1.18 の 非加算的モデルの平均平方の期待値の表でみると、 デザインが母数模型、変量模型、混合模型にかかわらず、ブロック因子との交互 作用に関する3つの項の平均平方の期待値 E(MS) が等しいことを意味し、その ためには、
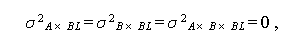
|
(2.23) |
が成り立たねばならないことがわかる。この結果は、この場合(すなわち、 大局的球形仮定が成り立つ場合)、われわれは加算的モデルを選択すべきである ことを意味する。
この場合のF比は、表 1.15 から、

|
(2.24) |
一方、Mauchly の検定により (2.22) 式の大局的球形仮説が棄却された としよう。その場合、われわれは非加算的モデルを選択することになるが球形 仮定は完全に否定できるかというと、そうではない。 大局的な球形仮定は成り立たずとも、部分的には球形仮定が成り立っているかも しれないのである。これが、局所的球形仮定である。 1.6.2 節のような2要因反復測度デザインの場合、局所的球形仮定は、表 1.15 の処理A、処理B、及びそれらの交互作用 A × B の3通り検討 しなければならない(ブロック因子は、反復測度ではないことに注意)。
まず、処理Aについては、局所的帰無仮説 (1.147) 式のもとで、局所的 球形仮説

|
(2.25) |
処理Bについても同様に、局所的帰無仮説 (1.148) 式のもとで、局所的 球形仮説

|
(2.26) |
最後に $A\times B$ については、局所的帰無仮説 (1.149) 式のもとで、 局所的球形仮説

|
(2.27) |
これらの帰無仮説はそれぞれ、もし採択されれば非加 算的モデルにおける当該 F比、すなわち (1.181) 式の F ' ともとの自由度で、棄却されれば表 1.17 の当該自由度を Box の ε 因子(実際には G-G Epsilon または H-H Epsilon) を用いて修正したうえで、同じく(1.181) 式の F ' を用いて処理要因の効果 の検定を行うとよい。図 2.1 は、これらの手順を図式化したものである。

|
最後に、2要因反復測度デザインでのサンプル数について述べると
| 大局的球形仮説が検定できるための必要条件は、サンプル数が水準の組み合わせ数 I×J マイナス 1 を下廻らないことである。 |
もっとも、上の問題点意外にも、SAS も SPSS も2要因反復測度デザインでは、 注意しなければならない重要な点がある。それは、既に 1.6.2 節の最後に指摘した ので省略する。