このページは、年3月29日に一部更新しました。
![]()
前々節と前節では、反復測度要因のみから成るデザインにおける球形検定について 述べた。とりわけ前節で述べた2要因反復測度デザインにおける大局的球形仮定 と局所的球形仮定及び球形検定の考え方は、3要因以上の要因がすべて反復測度 であるデザインに対しても自然に適用できる。
これに対して、1.7.2 節で述べたような、独立測度と反復測度が混在する デザインでは、球形仮説も球形検定も、前節でのようにはいかない。たとえば、 1.7.2節の2処理分割区画要因デザインで、反復測度型のサンプリングを行う 場合には、既に述べたように、まず独立測度としての処理Aの各水準に異なる 観測単位(被験者)群を無作為に割り付けるので、この水準ごとで反復測度と なる処理Bの水準間の相関関係は異なるものになる可能性がある。
Huynh and Feldt (1970) は、表 1.20 における処理B(反復測度要因) 及び A×B についての F 比が正確な F- 分布に従うための条件は、

|
(2.28) |
であり、この仮説は、

|
(2.29) |
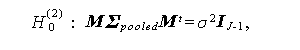
|
(2.30) |
の2つのステップで検定できることを示した。
ここで、Mは J -1行 J 列の直交正規対比行列、$\{\mbSigma_i,\; i=1,2,\cdots,I\}$は J 行 J 列の母共分散行列、I J-1 は J -1次の 単位行列である。また、$\mbSigma_{pooled}$は、
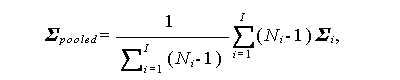
|
(2.31) |
(2.28)式は、多標本球形仮定 (multisample sphericity assumption) とか (Harris, 1984; Mendoza, 1980)、 多標本循環性仮定 (multisample circularity assumption) と呼ばれたりする (Mendoza, 1980; Kirk, 1982)。
(2.28)式の多標本球形仮定検定の検定統計量の雛形は、以下の帰無仮説

|
(2.32) |
この場合の、多標本球形仮説検討のための仮定のうち、(2.29)式に対応するのは

|
(2.33) |
である。
この場合、第一ステップの I 個の共分散行列の等質性の検定 (test for homogeneity of covariance matrices) には、つぎの Box (1949) の方法が使われる (Huynh and Feldt, 1970; Kirk, 1982)。 Kirk (1982) によれば、 この検定は Bartlett の分散の等質性の検定の拡張であり、非正規性に対しては 頑健でないという:

|
(2.34) |
ここで、

|
(2.35) |
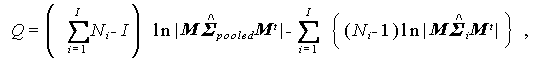
|
(2.36) |
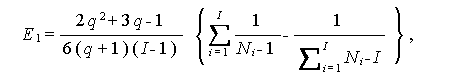
|
(2.37) |
であり、q は M の行数である(通常 q=J -1 )。
もし、N i が小さく q または I が大であれば、より正確な同じく Box によるつぎの F -検定が可能である (Kirk, 1982):

|
(2.38) |
ここで、
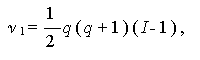
|
(2.39) |

|
(2.40) |
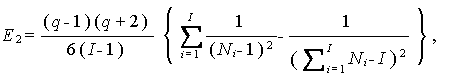
|
(2.41) |

|
(2.42) |
これに対して、第2ステップの (2.30) 式の検定には、Mauchly の球形 検定がそのまま使える。もちろん、この場合球形仮定が棄却されたとすると、 表1.8 の処理 B 及び A×B の効果の検定時の F- 分布の自由度は、 Box の ε 因子 (G-G Epsilon 又は H-F Epsilon) によって調整した ものを用いる。
最後に、共分散行列の等質性の検定について注意すべきことは、多標本 球形検定の文脈では2ステップ多標本球形検定の第1ステップとしての同等質性 の検定は、もとの反復測度変数に対してではなく正規直交化された 変数に対して行わねばならない点である。
後で見るように、まず SAS については、 ANOVA や GLM プロシジャには共分散行列の等質性の検定のオプションがないので DISCRIM プロシジャを用いる必要がある。そして、このプロシジャで pool=text なるオプションを選択すると、Box の χ2- 検定を行ってくれる。ただし、 多標本球形検定の文脈では、これを実行する前にあらかじめ data ステップを 組み、正規直交変数を作成しておく必要がある。
つぎに SPSS については、manova 文の print パラメータに homogeneity(box) なるオプションがあるので、これの指定を行えば共分散行列の等質性の検定を行える。 SPSS の場合は、χ2- 検定だけでなく F- 検定も 同時に出力されるので便利である。ただし、SAS の場合と同様、多標本球形検定 の文脈では、これを実行する前にあらかじめ compute 文を用いて正規直交変数を
最後に、任意の(反復測度)変数について簡単に正規直交変数化する方法を 紹介する。これについては、既に 1.7.3 節の最後に示したので、ここでは省略する。
いずれにせよ、多標本球形仮定を2ステップで検定する方法は、 2ステップ多標本球 形検定 (a two-step multisample sphericity test) と呼ぶことがで きる。一方、Mendoza (1980) は、多標本球形仮定 が1ステップで検定できることを示した。この方法は、 1ステップ多標本球形検定 (a single-step multisample sphericity test) と言える。
Mendoza (1980) の多標本球形検定は、つぎのようにして簡単に導ける:
まず独立測度としての処理 A の第 i 水準 (i =1, 2, ..., I ) に割り付け られた標本を xi1 , xi2 , ... , xiNi とする。この 標本が、N(\mbmu_i, \mbSigma_i) なる母集団(すなわち p 次元多変量正規 分布に従い、平均 $\mbmu_i$、共分散行列 $\mbSigma_i$ を持つ母集団)からの 無作為標本とすれば、密度関数 (density function) は、
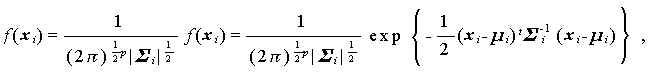
|
(2.43) |
したがって、尤度関数 (likelihoood function) は、
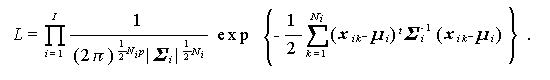
|
(2.44) |
つぎに、母平均 $(\mbmu_i,i =1,2,...,I ) なる I 個の母集団からの 標本 (xi1,xi2,...,xi Ni), i =1,2,...,I を手にしたとき、多標本球形仮説
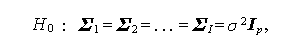
|
(2.45) |
のもとでの条件付き最大尤度 L(\omega) は、$\mbmu_i$ と $\mbSigma_i \; (i =1,2,...,I ) の条件付き最尤推定量 (conditional maximum likelihood estimators)
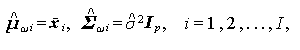
|
(2.46) |

|
(2.47) |
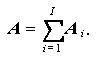
|
(2.48) |

|
(2.49) |
一方、無条件最大尤度 L(\Omega) は、$\mbmu_i$ と $\mbSigma_i,\quad (i =1, 2,...,I ) の無条件最尤推定量

|
(2.50) |
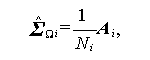
|
(2.51) |
したがって、尤度比は結局
|
もし、I =1 ならば、多標本球形仮定は、単純な球形仮定に帰着され、

|
(2.55) |
となる。(2.51) 式より、I =1 の時は、
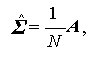
|
(2.56) |
であることに注意すれば、(2.53) 式の χυ2 は、 Mauchly の球形検定におけるもとの χ2、すなわち (2.12) 式に等し いことがわかる。
ここで、1要因反復測度の場合と同様、A には正規直交化された 変数に関するものを当てねばならないことに注意せよ。というのは、この場合も M が正規直交の場合には、(2.28) 式と (2.32) 式は同等ではあるが、球形 検定の (2.52) 式の λ の値は、もとの変数で計算する場合と、正規直交化され たものとでは、異なるからである。
ところで、(2.52)式の λ を、Mauchly の球形検定の場合と同様、 Box (1949) に従い修正することもできる (Mendoza, 1980)。修正された λ を λ* とすれば、
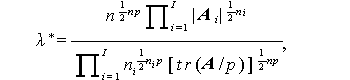
|
(2.57) |
ここで、

|
(2.58) |
さらに、λ* の分布は
の特性関数 (characteristic function) を用いての 積率 (moment) を近似することにより、近似 χ2- 統計量とみなせる。Mendoza によれば、
|
最後に、(2.57) 式の Mendoza (1980) の多標本球形検定は、実はその12年 前に Sugiura and Nagao (1968) が、それを含むより一般的な形で提案している のである。明らかに Mendoza は、Sugiura らの論文を見落していたことになる。 研究者の世界では、本来あってはならないことであるが、時々このようなことが 起こっているのである。
最後に、独立測度と反復測度が混在するデザインで、いずれか又は両方共2要因 以上の場合の球形検定にふれる。これに関しては、Kirk (1982) が詳しい。
このような場合、Kirk (1982) の用語法を用いれば、デザインは SPF-pr.q、 SPF-p.qr、SPF-ps.qr、... のように書ける。
このような場合の球形仮説を一般に

|
(2.61) |
とすると、まず L は、独立測度要因のすべての水準の組み合わせの数となる。 例えば、SPF-pr.q デザインでは、2つの独立測度要因の水準数は p 及び r なので、この場合 L=pr となる。SPF-prt.q デザインでは、L=prt である。
さらに、(2.61) 式の $\mbSigma_l$ の次数は、一般に反復測度要因の すべての水準の組み合わせの数である。例えば、SPF-pr.q デザインでは、 1つの反復測度要因の水準数は q なので、$\mbSigma_l$ の次数は q である。 これに対して、SPF-p.qr デザインでは、2つの反復測度要因の水準の組み合わせ 総数は qr なので、$\mbSigma_l$ の次数は qr である。
一方、(2.61) 式の M の列数は $\mbSigma_l$ の次数に等しいが、 M の行数は、大局的球形仮説の場合が $\mbSigma_l$ の次数マイナス1である 場合を除き、どの局所的球形仮説であるかにより変る。すなわち、一般に、このような 場合、多標本球形仮説は、大局的なものと局所的なものの2種類がある。もちろん、 反復測度要因が1つの場合、残りの独立測度がいくつあっても、大局的・局所的の 区別はなくなることは明らかである。すなわち例えば SPF-pr.q でも SPF-prt.q デザインでも、多標本球形仮説は (2.61) 式1つだけである。
とりわけ、SPF-pr.q デザインでは、独立測度を A、C、反復測度を B とすれば、区画間効果である処理 A、処理 C、交互作用 A×C は、通常の F- 検定 でよいが、区画内効果である処理 B 、A×B、 B×C、A×B×C の効果を見るための F 比の自由度は

|
(2.62) |
なる多標本球形仮説の検定により調整するかどうかをチェックしなければならない。
これに対して、SPF-p.qr デザインでは、独立測度要因を A 、2つの 反復測度要因を B 、C とすると、まず最初に大局的多標本球形仮説
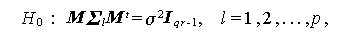
|
(2.63) |
の検定を、これが棄却された場合にはさらに、3組の区画内効果 (B, A×B)、 (C, A×C)、(B×C, A×B×C) をみるまえに、それぞれつぎの局所的多標本球形仮説

|
(2.64) |

|
(2.65) |
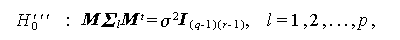
|
(2.66) |
の検定を行う必要がある。
より複雑な例えば SPF-pr.qt デザインの場合、独立測度要因を A 、C 、 反復測度要因を B 、D として、まず大局的多標本球形仮説は、
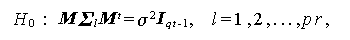
|
(2.67) |
つぎに、正確な F- 分布に従う区画間の効果、A、C、A×C に対して、つ ぎの3組の区画内効果、(B, A×B, B×C, A×B×C)、(D, A×D, C×D, A×C×D)、 (B×D, A×B×D, B×C×D, A×B×C×D) をみる前に、それぞれつぎの局所的多標本 球形仮説
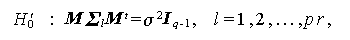
|
(2.68) |
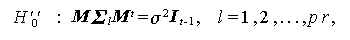
|
(2.69) |
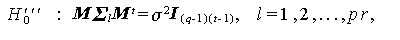
|
(2.70) |
の検定を行う必要がある。