このページは、平成２５年８月４日に開設しました。
このページは、令和２年４月７３日に一部更新しました。

2.1.6 節　Bartlett の球形検定と Mauchly の球形検定の違い

　これまでの節では、球形検定としては モクリー (Mauchly) のそれに限定 して述べてきた。しかし、球形検定には古くからもう１種類のバートレットの 球形検定 (Bartlett's sphericity tests) が知られている。さらに、同じ国際 的な統計ソフトである SAS では反復測定デザイン分散分析の出力中には Mauchly の 球形検定しか出てこないが、SPSS の同分散分析出力中には Bartlett のそれと Mauchly のそれの双方が出力されるので、注意が必要である。 さらに、例えば石村 (1997) の同デザインのSPSS 出力の解説 を見ると、両者を混同している記述があり、球形検定の初心者にとっては大変わか りにくい。
　そこで、この節では、まず Bartlett の球形仮説の概説を おこない、つぎにこれと Mauchly の球形検定との関係について述べる。なお、 最近の SAS、及び SPSS の日本語バージョンでは、球形検定を球面性検定と訳し ている。この問題点については、2-1-1 節で既に指摘したとおりである。
　従来、Bartlett の球形検定としては、現時点では筆者の知る限り、つぎの２つが知 られている：

相関行列の無相関性の検定 　複数の変数間の相関がすべてゼロかどうかの検定。変数間に（多変量）正規分布 が仮定される場合は、このことは変数間の独立性をも意味し、通常は「相関行列 の独立性の検定」と呼ばれることが多い。 モデルの残差共分散行列の球形性 　反復測定デザイン分散分析モデルの反復測定変数間の誤差項の球形性の検定。

2.1.6.1 節　相関行列の無相関性の検定

　Bartlett (1950) の相関行列の検定は、つぎの統計量が漸近的にカイ２乗統計量と なることを用いる：

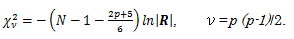
(2.71)

ここで、p は変数数、N はサンプル数、R は p 次の標本相関行列を表す。こ の検定は、上記 Bartlett (1950) によれば、Wilks (1932) までさかのぼる。
　Bartlett (1950) の相関行列の無相関性（独立性）検定は、SAS では最尤因子分 析における因子数の一連の検定の中での最初の部分、すなわち「共通因子はない」 (No common factors) なる帰無仮説の検定として用いられている。なぜならば、も し共通因子が１つもないのであれば、そのことは因子分析すべき変数間にはそれら に共通する変数は存在しない、つまり変数間は無相関であることになるし、逆に変数 間がすべて無相関であれば、それらに共通する因子、すなわち共通因子は存在しない ことになるからである。
　例えば、その具体例として筆者の WEB 上の講義ノート「データ解析/基礎と応用」第３章因子分析の中の 3.4.1 節 Table 2.3 の筆跡データへの適用例、のサイトの中の 最尤因子分析 における因子数の検定結果 を参照のこと。

2.1.6.2 節　モデルの残差共分散行列の球形性

　２つ目のバートレットの球形（球面性）検定は、SPSS の分散分析、とりわけ反復測 定デザイン分散分析で出力されるモデルの残差（誤差）に関する 共分散行列が球形性を持たないという帰無仮説の検定に用いられている (IBM Corporation, 1989)。
　まず、SPSS のマニュアルを見ると、この意味でのバートレットの球形（球面性）検 定は、行列 Y を反復測定デザイン分散分析データ、X をデザイン行列、 B を分散分析モデルのパラメータ行列とするとき、モデルの残差乗積平方和行列 (residual sums of squares and cross products) A に関するモクリーの球形 検定であることがわかる。ここで、SPSS マニュアルでは A をつぎのように表記 している：

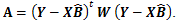
(2.72)

つまり、SPSS の反復測定デザイン分散分析でのバートレットの球形（球面性）検定では、 データに（反復測定）分散分析モデルを当てはめたとき、その誤差項が変数相互で無 相関であり、かつどの誤差変数の分散も等しい、かどうかを検定する。ここで、誤差変数 が正規分布に従えば、誤差項が変数間で相互に独立かどうかの検定とも言える。
　ちなみに、石村（1997, pp.36-37）では、まず「Bartlett の球面性の検定」の項に p.104 の分割区画型反復測定の例の出力のところには書かれている検定結果の注釈「 残差共分散行列が単位行列に比例するという帰無仮説を検定します」が（もとの SPSS の出力では出力されているにもかかわらず）抜けている。さらに、このことと一見 附合するかのように、p.37 では明らかな誤植がある、すなわち、

　正しくは、つぎのように書かないといけない：

　いずれにせよ、１要因反復測定デザイン分散分析の分析結果の一部 として出力される SPSS のパートレットの球面性検定は、同デザイン分散分析、と りわけ１変量分散分析（ANOVA）における要因の効果の有無の検定のための F-統計量の歪みの有無を検討するためのモクリーの球形検定（球面性検定）とは異なる ことに注意が必要である。なぜなら ば、モクリーの球形検定では、うえの石村の４変量データの場合、それらのモデルからの 残差の共分散行列ではなく、４変量データ自身間の共分散行列を正規直交行列により ３変量データに変換後の３変量共分散行列に対してモクリーの球形検定を施す必要が あるからである。

　石村の上の例は、１要因４水準の反復測定デザインデータ、すなわち乱塊法型の １要因反復測定デザインデータに対する分析例であるが、彼の著書の中の分割区画 型反復測定デザイン分散分析の例の場合の出力の説明（pp.104-105）にも同様な誤植が 見られる。すなわち、

　正しくは、つぎのように書かないといけない：

　最後に、上記の例にある分割区画型反復測定デザイン分散分析で１変量分散分析 すなわち ANOVA を用いる場合には、2.1.5 節で既に述べたように、多標本球形仮説 の検定が必要となるが、SPSS で出力されるモクリーの球面性検定に先立つボックスの 共分散行列の等質性に関する M 検定も、続いて出力されるバートレットの球面性検定 も、一見すると、順に多標本球形仮説の検定の第１ステップ、及び第２ステップで あるかのように誤解される可能性があるが、共に似て非なるものであることに注意 が必要である。
　その理由は、本ウエブページの 2.1.5 節の多標本球形仮説の２つのステップに対応する (2.29) 式、及び (2.30) 式を見れば明らかである。まず、(2.29) 式で表される同仮説の 第１ステップでは、SPSS が出力する石村の例に対する Box の M 検定で行うもとの３変量 間の共分散行列の等質性の検定ではなく、３変量データを正規直交化することにより得ら れる２変量変数の（被験者間要因の水準ごとの）共分散行列の等質性の検定を行う必要が あるからである。また、第２ステップについても、モクリーの球形検定を、SPSS が出力す る石村の例に対する３変量の残差共分散行列に対してではなく、複数の被験者間要因の水 準ごとの共分散行列をプールした後に正規直交化したものに対して施す必要があるからで ある。