| 1.コーエンの一致係数 |
| 2.コーエンの重み付き一致係数 |
| 3.コーエンの条件付き一致係数 |
| 4.フリードマンの方法 |
| 5.フリードマンの正確な検定法 |
| 6.エベルの一致係数(信頼性係数) |
| 7.フライスの一致係数 |
この節には、つぎの2つの SAS プログラムのダウンロードコーナーがあります:
| 1.Ebel の一致係数用 SAS プログラムの例1 |
| 2.Ebel の一致係数用 SAS プログラムの例2 |
このページは、平成21年12月27日に開設しました。
このページは、平成30年7月24日に一部変更しました。
![]()
社会行動科学、とりわけ心理学や教育学では、複数の条件に対して同一人や同一グループ が反応させられる場合や、数人の教師が複数の生徒のそれぞれに対する評価を行う場合がしばしば ある。このようにして得られたデータに対して、現在では、反復測定デザ イン分散分析 等の数理統計学的方法がほぼ確立しており、一般的にはこれらの方法を用い ることが望ましいと思われるが、このようなデータに対しては、伝統的には(反復測定デザイン ANOVA 等の方法が70年代から発展する以前から)幾つかの方法が知られており、この節では今後 それらの方法を簡単にレビューし、反復測定デザイン分散分析やその他関連する研究との関連につ いても触れる。当面は、古いほうの論文からまとめる。
コーエンの一致係数(Cohen, 1960) は、n人の対象に対する2名の評定者の評定 結果の一致度や、同一質問紙による繰り返し調査の一致度をみるためのものである。 評定結果は、名義尺度で k 個の独立で相互に排反、かつすべてを尽くしている(悉皆)(independent, mutually exclusive, and exhaustive) カテゴリーから成るものとする (Cohen, 1960, p.38)。
ここで、fij は、評定者 A が(複数の)対象を k 個の評定カテゴリーのうちの第 i カテゴリー に属すると判定し、かつ評定者 B が(複数の)対象を k 個の評定カテゴリーのうちの第 j カテゴリー に属すると判定した場合の度数を表す。
一方、pij は、評定者 A が(複数の)対象を k 個の評定カテゴリーのうちの第 i カテゴリー に属すると判定し、かつ評定者 B が(複数の)対象を k 個の評定カテゴリーのうちの第 j カテゴリー に属すると判定する確率を表す。以下の (3.1) 式で表されるコーエンの一致係数κは、母集団でのそれを、 また、(3.2) 式で表されるκの推定値は、標本でのそれである:
1) 定義
対応するカテゴリーの観察頻度が一致する確率を p0,
対応するカテゴリーが偶然により一致する確率を pc とする時、

|
で、一致係数κは、
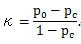
|
(3.1) |
一方、κの標本に基づく推定値は、

|
(3.2) |
2) 検定
上式のκの推定値の漸近分散が知られており、κ=0 なる帰無仮説のもとでは、当該漸近分散 も計算できるので、これを用いて帰無仮説の検定が可能である。
(3.2) 式では、一致度を見るのは対角要素のみで、非対角要素については 考慮されていない。各セルごとに一致の重要性を評価し重み(wij) をつける方法が、コーエ ンの重み付きκである。
1) 定義
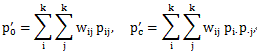
|
とする時、重み付きカッパκwは、
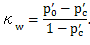
|
(3.3) |
一方、κの標本に基づく推定値は、

|
(3.4) |
2) 検定
上式のκwの推定値の漸近分散が知られており、κw=0 なる帰無仮説のもとでは、 当該漸近分散も知られているので、これを用いて帰無仮説の検定が可能である。
2名の評定者の一致度を考える時、一方の評定値を基準に取り、それに対して他方の評定値が どの程度一致しているのかを考えたい時、次のκをカテゴリー i の条件付 一致係数という:
1) 定義

|
(3.5) |
一方、κの標本に基づく推定値は、
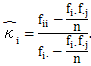
|
(3.6) |
この式が多項分布標本のもとでの最尤推定値であることは、Bishop et al. (1975) が指摘している。
2) 検定
上式のκiの推定値の漸近分散が知られており、κi=0 なる帰無仮説のもとでは、 当該漸近分散も知られているので、これを用いて帰無仮説の検定が可能である。
註
統計学辞典にある上記3つの一致係数は、すべてデータが名義尺度でかつ2名の評定者 間の一致度を表すための指標である。これに対して、Bishop et al. (1975) には、2名以上の評定者 間の一致度の指標として Lin (1974) があげられているが、この論文は PhD. dissertation であり、入手が 難しい。
一方、岩原 (1975) にあげられているつぎの2つの指標は、順序尺度でかつ2名以上の評定者による評定対象 間の順位の一致度を表すためのものである。
複数の条件に対して同一人やグループが測定される時や、数名の教師が同じ生徒に対する評定をする場合、 (反応は独立でなく)、かつデータが順序尺度の場合の方法の1つである。ここで、 生徒数は n とする:
1) 定義
条件数や検査実施日を p 個とする時、検定に用いられる p 個の統計量を T1, T2, ..., Tp と書けば、これらの統計量は、つぎの表の各列の合計である。ここで、表中の r は順位を表し、 各生徒 P ごとに、テスト実施日による得点の順位をつけるものとし、同順位はないものとする。つまり、表中 順位は行ごとにつけられているとする:
| 生徒 | p 個のテスト実施日 | 計 |
| P1 | r11 , r12 , ... , r1p | p(p+1)/2 |
| P2 | r21 , r22 , ... , r2p | p(p+1)/2 |
| . | .............. | . |
| Pn | rn1 , rn2 , ... , rnp | p(p+1)/2 |
| 計 | T1 , T2 , ... , Tp | p(p+1)/2 |
2) 検定
H0:検査実施日により生徒の成績の順位は変わらない、なる帰無仮説のもとでは、つぎの χ2 が近似的に自由度 p-1 のχ2 分布に従うことを利用する:
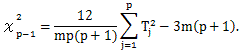
|
(3.7) |
註
岩原新訂版 (1999, p.232) には、フリードマンの直接の引用文献は記されていないが、そこで引用 されている岩原 (1964)「ノンパラメトリック法」の第5版 (1970) を見ると、直接の引用文献は Friedman (1937) であることがわかる。
この検定法については、岩原 (1975) には、そのための別表 XIV が引用されている。これは、 Friedman (1937) の論文より転載されたものである。
註1
ここで、(3.7) 式のχ2 と同上の岩原新訂版30.4B にある順位の一致係数

|
(3.8) |
との間には、
|
|
(3.9) |
の関係がある。ここで、もし p=2 ならば、この検定はサインテストになる。
註2
(3.8) 式の一致係数は、肥田野ら (1961, p.171) にある一致係数に等しい。肥田野らは、この ページの脚注で Kendall (1962) を引用しているものと思われるが、W はたぶん Hollander & Wolfe (1973) で引用されている Kendall (1938) の可能性が高い。
Ebel の方法では、生徒に対する2名以上の評定者の評定データ(間隔尺度レベル)を仮 定し、評定者間の一致度の測度を用いる。Ebel は、この方法を平均評定の信頼性 (the reliability of the average ratings) を見るためのものとみなす。この方法でのデータの一般形を示したのが、表 3.2である。この表で、行には n 人の生徒が、列には k 人の評定者が割り当てられているとする。また、第 i 生徒 に対する第 j 評定者の成績等の評定結果を xij と表記するものとする。
| 生徒 | k 人の評定者 |
| P1 | x11 , x12 , ... , x1k |
| P2 | x21 , x22 , ... , x2k |
| . | .............. |
| Pn | xn1 , xn2 , ... , xnk |
Ebel は、3つ以上の評定の信頼性の指標として Peters & Van Voorhis (1940)、Snedecor (1946)、及び Horst (1949) の指標を検討した結果、Fisher (1946) の級内相関 (intraclass correlation) の方法を 応用した Snedecor (1946) の指標が最も便利で一般的に有用であるとし、Snedecor のつぎの指標を推奨している:
1) 定義

|
(3.10) |
ここで、上式の MSP、及び MSEは、表3.2のデータで生徒を要因とする完全無作為化デザイン 分散分析 (CR-n ANOVA) とみなした場合における、順に、要因に関する平均平方 (mean squares)、及び誤差に関する平方 平均を表す。また、k は、表 3.2 のような釣り合い型デザインの場合、生徒要因の各水準のサンプル数(評定者数)である。
2) 区間推定
Ebel は、うえの指標 r1 の信頼区間を、F=MSP/MSEなる関係 が成り立つことを利用して求める方法も示している。
3) SAS を用いた適用例
適用例1(Ebel, 1951)
(i) データ
ここでは、Ebel に掲載されているデータ例等を SAS を用いて分析した結果を示す。また、そのため の SAS プログラムも示す。最初の例は、Ebel の Table 1 (p.411) のデータに対するものである。表 3.3はこれを示す。
| 生徒 | 2人の評定者 |
| P1 | 3, 1 |
| P2 | 1, 3 |
| P3 | 5, 4 |
| P4 | 4, 5 |
(ii) SAS プログラム
つぎのプログラムは、上記データを Ebel による信頼性の指標計算のためのSASプログラムである。
*-------------------------------------------------------------------------*
| July 20, 2009 |
| sas program -- CR2-4-Ebel-Table1.sas |
| |
| An example of a CRp-q ANOVA design analysis for Ebel (1951) Table 1 |
| data (p.411). |
| |
*-------------------------------------------------------------------------*;
options ps=60 ls=80;
/* (1) data input */
data work;
do pupil=1 to 4;
do rater=1 to 2;
input y @;
output;
end;
end;
label rater='rater'
pupil='pupil'
y='scale value';
cards;
3 1
1 3
5 4
4 5
;
/* (2-1) CR2-4 ANOVA using proc anova */
title 'CR2-4 ANOVA for the Ebel (1951, p.411) data';
proc anova data=work;
class rater pupil;
model y=rater pupil;
means rater pupil/tukey alpha=0.01;
/* means rater pupil/tukey cldiff alpha=0.01; */
run;
/* (2-2) Means plot using proc means output */
title 'means of each rater of the factor';
proc means data=work;
var y;
class rater;
output out=temporal mean=mrater;
run;
options ps=30 ls=80;
proc plot data=temporal;
plot mrater*rater;
run;
title 'means of each pupil of the factor';
proc means data=work;
var y;
class pupil;
output out=temporal mean=mpupil;
run;
options ps=30 ls=80;
proc plot data=temporal;
plot mpupil*pupil;
run;
/* (3-1) CR2-4 ANOVA using proc glm */
options ps=60 ls=80;
title 'CR2-4 ANOVA by proc glm';
proc glm data=work;
class rater pupil;
model y=rater pupil;
means rater pupil;
means rater pupil/tukey alpha=0.01;
lsmeans rater pupil;
run;
|
うえのプログラムでは、順に以下の処理を行うが、このプログラムでは Ebel の一致係数(信頼性係数)までは算出していないことに注意せよ:
上記 anova プロシジャは、釣り合い型デザインの場合の分散分析のためのものであるが、 ここでは、同一データを非釣り合い型デザインの場合の分散分析のための glm プロシジャ により分析する。この例のような釣り合い型の場合、結果は anova プロシジャと同一であるので、 この部分は不要である。
| CR2-4-Ebel-Table1.sas |
(iii) SAS プログラムによる出力結果
うえのプログラムを実行すると、以下のような出力結果が得られる。結果のうち、Tukey 法に よる多重比較の結果は、ここでは不要なので省略した:
CR2-4 ANOVA for the Ebel (1951, p.411) data 1
2010年01月04日 月曜日 午後12時26分59秒
ANOVA プロシジャ
分類変数の水準の詳細
分類 水準 値
rater 2 1 2
pupil 4 1 2 3 4
読み込んだオブザベーション数 8
使用されたオブザベーション数 8
CR2-4 ANOVA for the Ebel (1951, p.411) data 2
2010年01月04日 月曜日 午後12時26分59秒
ANOVA プロシジャ
従属変数: y scale value
変動因 自由度 平方和 平均平方 F 値 Pr > F
Model 4 12.50000000 3.12500000 1.88 0.3164
Error 3 5.00000000 1.66666667
Corrected Total 7 17.50000000
R2 乗 変動係数 誤差の標準偏差 y の平均
0.714286 39.72291 1.290994 3.250000
変動因 自由度 Anova 平方和 平均平方 F 値 Pr > F
rater 1 0.00000000 0.00000000 0.00 1.0000
pupil 3 12.50000000 4.16666667 2.50 0.2358
|
うえの結果のうち、(3.10) 式の Ebel の推奨する一致係数(信頼性係数)を求め るために必要な値のうち、pupil 要因の平均平方が MSP であり 4.1667、誤差要因 Error の平均平方が MSE であり 1.6667 である。また、本来の要因 pupil の各水準 のサンプル数(評定者数)が (3.10) 式の k なので2であり、これらの値を (3.10) 式に代入 すれば、スネディガー方式のEbel の一致(信頼性)係数は、
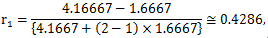
|
(3.11) |
となる。
このデータの場合、たまたま評定者間のばらつきは rater の平方和をみれば明らかなように ゼロであるので、誤差項から評定者間のばらつきを除いても除かなくても、同じ結果になる。
means of each rater of the factor 5
2010年01月04日 月曜日 午後12時26分59秒
MEANS プロシジャ
分析変数 : y scale value
オブザべーション
rater 数 N 平均 標準偏差 最小値
--------------------------------------------------------------------------------
1 4 4 3.2500000 1.7078251 1.0000000
2 4 4 3.2500000 1.7078251 1.0000000
--------------------------------------------------------------------------------
分析変数 : y scale value
オブザべーション
rater 数 最大値
----------------------------------------------
1 4 5.0000000
2 4 5.0000000
----------------------------------------------
|
省略。
means of each pupil of the factor 7
2010年01月04日 月曜日 午後12時26分59秒
MEANS プロシジャ
分析変数 : y scale value
オブザべーション
pupil 数 N 平均 標準偏差 最小値
--------------------------------------------------------------------------------
1 2 2 2.0000000 1.4142136 1.0000000
2 2 2 2.0000000 1.4142136 1.0000000
3 2 2 4.5000000 0.7071068 4.0000000
4 2 2 4.5000000 0.7071068 4.0000000
--------------------------------------------------------------------------------
分析変数 : y scale value
オブザべーション
pupil 数 最大値
----------------------------------------------
1 2 3.0000000
2 2 3.0000000
3 2 5.0000000
4 2 5.0000000
----------------------------------------------
|
省略。
この例は分散分析デザインとしては釣り合い型であるが、データが非釣り合い型の場合には、 SAS の場合 anova プロシジャでなく、上のプログラムにあるような glm プロシジャを用いなけれ ばならない。しかし、この例は釣り合い型デザインなので、結果は省略する。
適用例2(河合, 2009)
(i) データ
ここでは、河合(2009)のデータの1つを SAS を用いて分析した結果を示す。また、そのため の SAS プログラムも示す。つぎの表は、河合のデータの1つである。このデータは、不登校児に 対するあるグループ体験の初年度参加者16名に対して、参加スタッフ3名が「他者がどのような価値観 を持っているか、どのような考えを持っているかを知る」レベルを5件法の評定尺度で評定した結果である。
| 生徒 | 3人の評定者 |
| P1 | 2,1,1 |
| P2 | 3,3,3 |
| P3 | 2,3,3 |
| P4 | 4,5,4 |
| P5 | 2,1,1 |
| P6 | 2,3,2 |
| P7 | 3,1,3 |
| P8 | 2,1,2 |
| P9 | 1,1,1 |
| P10 | 3,3,3 |
| P11 | 2,1,2 |
| P12 | 2,1,4 |
| P13 | 3,1,3 |
| P14 | 2,4,3 |
| P15 | 4,3,4 |
| P16 | 5,3,5 |
(ii) SAS プログラム
つぎのプログラムは、上記データに対して Ebelの一致係数の指標、 及びその95%信頼区間を計算するためのSAS プログラムである。プログラムの最初のコメント欄に記したように、このプログラムでは、 評定者 c は3、Ebel の一致係数の信頼区間計算時の信頼度 pconf は95%であることに注 意せよ。もし、これら2つの値を変更したい場合は、利用者の方で、以下のプログラム中の 最初の data ステップの中の数字3、anova プロシジャの中の title 分の中の CR16-3 の3、 及び4つ目のdata ステップの中の数字3をすべて利用者の場合の評定者数に変更すること。 さらに4つ目のdata ステップの中の pconf の値を必要な信頼度に変更せよ。
*----------------------------------------------------------------------------*
| January 14, 2010 |
| sas program -- CR16-3-kawai6.sas |
| |
| Example of a CR-p-q ANOVA design analysis for Kawai data. |
| In this program, users must change the values of the following two param- |
| eters: |
| (1) c ------- the number of items to which raters responded, |
| (2) pconf --- the confidence level for the Ebel reliability coefficient. |
| |
*----------------------------------------------------------------------------*;
libname sasfile 'c:\permfile';
options ps=60 ls=80;
data work;
set sasfile.kawai6;
array x{3} var1-var3;
do rater=1 to 3;
y=x(rater);
if rater=1 then pupil+1;
output;
end;
run;
title 'CR16-3 ANOVA for Kawai data';
proc anova data=work outstat=workout;
class rater pupil;
model y=rater pupil;
means rater;
run;
title 'means of each rater of the factor';
proc means data=work;
var y;
class rater;
output out=temporal mean=mrater;
run;
options ps=30 ls=80;
proc plot data=temporal;
plot mrater*rater;
run;
proc print data=workout;
run;
data work2;
set workout;
if _SOURCE_='rater' or _SOURCE_='pupil' then delete;
dfe=df; sse=ss; m=sse/dfe;
run;
data work3;
set workout;
if _SOURCE_='ERROR' or _SOURCE_='rater' then delete;
dfp=df; ssp=ss; mp=ssp/dfp;
run;
data work4;
merge work2 work3;
c=3; cmo=c-1;
r=(mp-m)/(mp+cmo*m);
fs=mp/m;
pconf=0.95;
ft=finv(pconf,dfp,dfe);
fpu=fs*ft; fpl=fs/ft;
rupper=(fpu-1)/(fpu+cmo);
rlower=(fpl-1)/(fpl+cmo);
run;
proc print data=work4;
var mp m fs ft fpu fpl rlower r rupper;
run;
|
| CR16-3-kawai6.sas |
(iii) SAS プログラムによる出力結果(最初と最後のみ)
うえのプログラムでは、出力の最後に、Ebel の一致係数 (信頼性係数)や、その95%信頼区間を出力する。ここでは以下に、途中の出力結果は省略し、 最初と最後の出力部の2か所のみ表示する:
CR16-3 ANOVA for Kawai data 62
2010年01月14日 木曜日 午後06時34分20秒
ANOVA プロシジャ
分類変数の水準の詳細
分類 水準 値
rater 3 1 2 3
pupil 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
読み込んだオブザベーション数 48
使用されたオブザベーション数 48
CR16-3 ANOVA for Kawai data 63
2010年01月14日 木曜日 午後06時34分20秒
ANOVA プロシジャ
従属変数: y
変動因 自由度 平方和 平均平方 F 値 Pr > F
Model 17 48.77083333 2.86887255 5.00 <.0001
Error 30 17.20833333 0.57361111
Corrected Total 47 65.97916667
R2 乗 変動係数 誤差の標準偏差 y の平均
0.739185 30.04448 0.757371 2.520833
変動因 自由度 Anova 平方和 平均平方 F 値 Pr > F
rater 2 2.79166667 1.39583333 2.43 0.1049
pupil 15 45.97916667 3.06527778 5.34 <.0001
CR16-3 ANOVA for Kawai data 64
2010年01月14日 木曜日 午後06時34分20秒
ANOVA プロシジャ
水準 --------------y--------------
rater N 平均 標準偏差
1 16 2.62500000 1.02469508
2 16 2.18750000 1.32759180
3 16 2.75000000 1.18321596
|
OBS mp m fs ft fpu fpl rlower r rupper 1 3.06528 0.57361 5.34383 2.01480 10.7668 2.65228 0.35516 0.59149 0.76501 |
この最後の出力結果のうちの右から2つめの r=0.59149 が一致係数であり、その95 %信頼区間は(rlower, rupper) すなわち (0.35516, 0.76501) である。
フライスの一致係数は、コーエンの一致係数を3名以上の評定者の場合に拡張するものである。 評定結果はコーエンの場合と同様に、名義尺度で k カテゴリーから成るもの とする。また、N 人の生徒に対する当該名義尺度での n 人の評定者の評定結果は、つぎのような 表にまとめられる。ここで、表中 fij は、第 i 生徒に対して n 人の評定者のうち評価を 名義尺度の選択肢のうちの第 j カテゴリーに該当するとした者の人数(度数)である:
| 生徒 | k カテゴリーへの評定度数 |
| P1 | f11 , f12 , ... , f1k |
| P2 | f21 , f22 , ... , f2k |
| . | .............. |
| PN | fN1 , fN2 , ... , fNk |
1) 定義
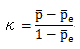
|
(3.12) |
ここで、
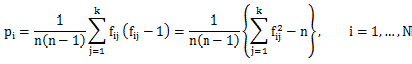
|
(3.13) |
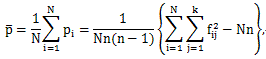
|
(3.14) |
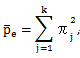
|
(3.15) |
|
|
(3.16) |
註1 (3.13)式の piは、各生徒について n 人分の評定が2対の評定者の可能な割り当て 対 nC2=n(n-1)/2 個に対する、個々のカテゴリーへの評定が一致する数 ni1, ni2, ..., nik のそれぞれにおける2対の評定者が一致する数nij C2=nij(nij-1)/2 個 の和の比率を意味する。つまり、各生徒ごと の、評定者(n 人)の一致率を表している。
註2 (3.15)式の値は、もし評定者 n 人の評定が完全にでたらめになされたとする時、評定の平均的 な一致率は、各カテゴリー j では、評定者にかかわらずそのカテゴリーが選択される比率は全体の 比率πjに等しく、かつ独立であると考えると、πj の2乗となる。そこで、 全カテゴリーでの平均的一致率は、当式のようになる。
2) 検定
評定に一致が見られず、さらに N が大で生徒間でΣj=1knij 2, i=1, ..., N が相互に独立とみなされる時、SE(κ) をκの標準誤差とすると、
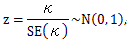
|
(3.17) |
が成り立つことを用いる。ここで、
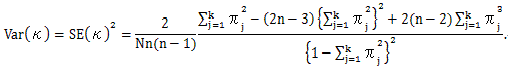
|
(3.18) |
3) 適用例
(i) データ
ここでは、河合(2009)のデータの1つを分析した結果を示す。つぎの表は、河合のデータの1つ である。このデータは、不登校児に対するあるグループ体験の初年度参加者16名のそれぞれが体験後に記し た文集の内容に対して、参加スタッフ及び分析者の合計3名が評価した7つの視点のうちの1つである、 「メンバーやスタッフから受容され」ていた(肯定的)か、否(否定的)かの結果である。表中の各参加者 に対する2つの値は、順に、3名の評定者のうち肯定的と評価した者の度数、及び否定的と評価した者の度数 を示す。
このデータでは、評定者は3名で、評定カテゴリーは肯定的か否かの2値(2カテゴリー)である。
| 参加者 | 2カテゴリーへの評定度数 |
| P1 | 3, 0 |
| P2 | 3, 0 |
| P3 | 1, 2 |
| P4 | 2, 1 |
| P5 | 2, 1 |
| P6 | 3, 0 |
| P7 | 3, 0 |
| P8 | 2, 1 |
| P9 | 1, 2 |
| P10 | 1, 2 |
| P11 | 2, 1 |
| P12 | 3, 0 |
| P13 | 3, 0 |
| P14 | 3, 0 |
| P15 | 3, 0 |
| P16 | 3, 0 |