| 3.2.1級内相関とは |
| 3.2.2級内相関係数とエベルの一致係数との関係 |
| 3.2.2 3.2.3 節 級内相関と反復測度デザイン分散分析との関係 |
このページは、平成22年1月22日に開設しました。
このページは、令和2年4月27日に一部変更しました。
![]()
Ebel (1951, p.408) によれば、級内相関係数 (intraclass correlation) は、Fisher (1946) によるという。Snedecor & Cochran (1967)(畑村ら, 1972) によれば、まずつぎの 表3.7のようなデータ、すなわち各級に n 個の成員を含む一元分類を考えるとする:
| 級 | n 人の成員の測定値 |
| 1 | x11 , x12 , ... , x1n |
| 2 | x21 , x22 , ... , x2n |
| . | .............. |
| a | xa1 , xa2 , ... , xan |
ここで、級内相関のモデル(構造模型)は、つぎのようである:
(1) Xij = μ + Eij, Eij = N(0, σ2),
(2)同一級間の2人の成員は、共通の相関係数ρI(級内相関係数)を持つ。
彼らによれば、この種のモデルは分散分析より前に世に出ているという。
ここで、表3.7のデータを水準が a 個から成る1要因の通常の分散分析、すなわち完全無作為化 デザインデータとみなせば、当該要因の主効果にかかわる平均平方 uAや誤差に関する平均 平方 uEの期待値、E(uA)及び E(uE) は、 1.3節 完全無作為化デザインと多重比較、の表1.3 の右端の値のように書けるが、うえの級内相関の構造模型からは、それらは、uA や uE の定義式に構造模型の右辺を代入して整理すれば、つぎのように書ける:
|
|
(3.23) |
|
|
(3.24) |
また、ρI の推定値 rI は、
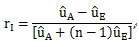
|
(3.25) |
と書ける。ここで、
|
|
(3.26) |
級内相関係数関連で、現時点で少しまとまった紹介がきちんとなされている WEB サイトとしては、 当ページの最後に紹介する下井、森川、対馬のものなどがあり、これら3点については pdf ファイル もしくは ppt ファイルが入手可能である。
前節の級内相関係数の推定式(3.25)式の右辺の各項を
|
|
(3.27) |
のように読みかえると、前節のエベルの一致係数の定義式 (3.10) 式に等しいことは明らか である。もちろん、Ebel (1951) は(3.25) 式が Snedecor (1946) によるものであることを 指摘している。つまり、エベルの一致係数(信頼性係数)とは、スネディカーの級内相関 係数に他ならない。Ebel (1951) は、それまでにフィッシャーが提案した級内相関係数に対して 複数の研究者が提案した推定方法を比較検討し、スネディカーの方法が最も便利で有用である と結論付けた。
3.2.1 節の級内相関の定義から明らかなように、級内相関のモデルは各級の n 個の測定値に対して 複合対称性(compound symmetry) を仮定している。複合対称性は、分散分析モデルでは F 分布 が歪まないための十分条件であり(例えば、Huynh & Feldt, 1970; Kirk, 1985)、表 3.6 のような 級内相関のためのデータを分散分析モデルで分析しても、主効果の F 比は歪まない。もちろん、分散 分析モデルで F 分布が歪まないための必要十分条件は、複合対称性ではなく、第2章 反復測度分散分析 、のところで述べた球形仮説(本邦では、球面性仮説、と表現されることが多い)が成り立つことであ る。
級内相関のモデルでは、例えば Snedecor and Cochran (1967) における双生児の各人の両手の指紋 の条数などの特別な測定値が想定されている。この例のような場合でさえ、級内相関の構造模型をデータ に適用するためには、この種のデータに対して果たして複合対称性が成り立っているのかどうかの検討 が必要であろう。既に第2章でも述べたように、分散分析における F 分布が歪まないための必要十分 条件が証明されたのは、Fisher (1946) が級内相関の概念を提案し、Ebel (1951) らの一致係数が議論 されてからかなりの年月が経った 1970 年(Huyneh & Feldt, 1970; Rouanet & Lepin, 1970) であり、 現時点では、例えばEbel らの一致係数を計算する前に、果たして表 3.6 の形のデータが複合対称性や 球形仮説(球面性)を満たしているのかどうかを検討する必要があろう。また、もしデータが複合対称 性を満たしていなくても球面性を満たしている場合、スネディカーやエベルに代わる一致性係数は考え られないかの検討も必要であろう。