第2章 行列・行列式の数学的基礎のホームページへようこそ
![]()
![]()
この頁は、平成16年7月22日に新たに開設しました。
この頁は、令和2年5月158日に一部更新しました。
ここでは、本書で扱う数学的概念のうち、行列とベクトルに限定してそれらの 定義や定理などの数学的基礎について述べる。第1節ではまず行列の定義を行う。 第2節では、正方行列、対称・非対称行列、歪対称行列、転置行列、下側・上側三角 行列、対角行列、単位行列、エルミート行列、行ベクトル、列ベクトル、位置 ベクトルの定義を示す。第3節では、行列の加減乗除、行列とスカラーの積につい ての説明を行う。第4節では、行列式の定義と例、及び行列式と正則行列との関係 について述べる。第5節では、ベクトル空間の定義を行い、そこでの一次従属性、次 元、基、及びノルムについて説明する。第6節では、線型空間の定義と一次変換につ いて述べる。第7節では、行列の基本操作と階数について述べる。第8節では、固有 値問題の説明と、固有値問題の基礎定理を列挙し、最後に正方行列の標準形について の定理をあげる。第9節では、双一次形式の定義、二次形式及びエルミート形式とそ の符号について説明する。第10節では、特異値分解について説明する。最後の第11 節では、テンソルについて簡単にふれる。これらの中には幾つかの定理が含まれるが、 それらの証明は本書の目的から外れるので、すべて省略する。これらの数学的基 礎は、行列や代数については浅野 (1966)、奥川 (1966)、Lancaster and Tismenetsky (1985)を、空間論全般については Bowen and Wang (1976) を、参考にした。
行列 (matrix) とは、日常的な言葉を用いるならば、 数字を行 (row) と列 (column) に並べたもので、 つぎのように書かれる。
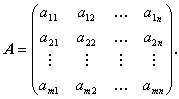
| (A.1) |
行列は、その第 j 行 k 列要素 ajk を用いて、 つぎのようにより簡潔な形で書かれることもある:
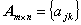
| (A.2) |
この場合には、ただし行列 A の行数と列数を (A.2) 式のように A の
下に m ×n として明示することがある。
日常的な言葉を用いるならば、行列の定義は、上のようでよいが、数学的
にはこれでは不十分であり、行列の要素がどのような性質を持っているか
の定義が必要となる。一般的には、行列の各要素 ai j は、任意の
数体 (number field) に属していないといけない。
ここでいう「数体」とは、なんらかの数 (number) の
集合 (set) に対して、その範囲内で加減乗除の四則演算が
ゼロによる除法を除き自由に行われるような集合をいう。本書ではその一部である
実数 (real number) もしくは
複素数 (complex number) のいずれかに限定する。一般に、その要素が
実数のみから成る行列は、実行列 (real matrix)、
同じく複素数から成る行列は、複素行列 (complex matrix) と呼ばれる。
もちろん、本書で扱う主要な行列の要素は、任意の対象相互の(非)類似度判断デー
タであり、実数でしかない。しかし、本書の主題である非対称MDSを理論的に検討
する場合には、本書で展開するように複素数を導入することがたいへん便利である
ばかりでなく、われわれが対称な距離空間の範囲で非対称関係を分析する場合には、複
素空間の導入は論理的帰結なのである。
前節で述べた行列は、その要素が定数であろうが複素数であろうが、行数と列数が異なるので、
矩形行列 (rectangular matrix) と呼ばれる。
(矩形)行列の要素がすべてゼロの時、その行列はゼロ行列 (zero matrix) と呼ばれ、
O と表される。
これに対して、行数と列数が等しい行列は、正方行列 (square matrix) と呼ばれる。
正方行列の要素のうち、対角部分の要素、a11 , a22 ,... は、
主対角要素 (main diagonal element) と呼ばれる。
本書でのN個の対象相互の(非)類似度判断データは、
正方行列 S ={ sjk } にまとめられる。ここで、一般に n 行 n 列の
正方行列のことをn 次の正方行列 (square matrix of order n ) と
呼ぶことがある。
正方行列 A の第 j 行 k 列の値 ajk と第 k 行 j 列
の値 ak j は、一般的には必ずしも等しくない。
このような行列を、非対称行列 (asymmetric matrix) と呼ぶ。
本書の主題である非対称MDSにおけるN次の正方行列は、まさにこの非対称行列に他ならない。
一方、正方行列のすべての対 ( ajk ,ak j )について
ajk = ak j が成り立つ行列は、
対称行列 (symmetric matrix) と呼ばれる。
ここで、任意の正方行列 A は、一意的につぎのように分解できることに注意されたい:
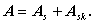
| (A.3) |
ここで、
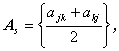
| (A.4) |
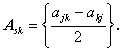
| (A.5) |
もちろん、As 、Ask の定義 (A.4) 式及び
(A.5) 式から、As は対称行列であり、Ask
は非対称行列であることは明らかである。
(A.5)式より、Ask は非対称行列であるばかりでなく、その第 j
行 k 列要素と第 k 行 j 列要素は符号が反対になっていることがわかる。
そのような行列は一般的に、歪対称行列 (skew-symmetric matrix
又は anti-symmetric matrix) と呼ばれる。本テキストで複素行列を定義するに先立ち、われわれ
はまず類似度行列 S を (A.3)式によりその対称部と歪対称部に分解する。
(A.1)式で書かれる任意の行列のすべての行をそっくりすべての列に置き換えた行列は、
(行列 A の)
転置行列
(transposed matrix)
と呼ばれ、At もしくは A ’と書かれることが多い。
At を (A.1)式のように表現すると
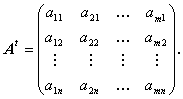
| (A.6) |
となる。当然、At は n 行m 行の行列となる。
n 次の正方行列で、つぎに示す Al ,Au のように、
その主対角要素の上側および下側がすべてゼロである行列は、それぞれ下側三角行列
(lower triangular matrix)および上側三角行列 (upper triangular matrix)
と呼ばれる:
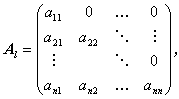
| (A.7) |
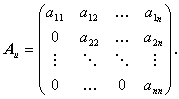
| (A.8) |
もし、行列 A が対称行列ならば、つぎの関係が成り立つことは自明である:
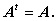
| (A.9) |
また、同じく n 次の正方行列のうち、その対角部分のみ値があり、 非対角部分はすべてゼロのような行列、すなわち
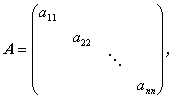
| (A.10) |
なる行列は、対角行列 (diagonal matrix) と呼ばれる。もちろん、(A.10) 式で空白になっている要素は、すべてゼロとする。
対角行列は、しばしば (A.10) 式の形でなく
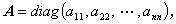
| (A.11) |
と書かれる。
対角行列の特別なケースの1つは、対角要素がすべて1なる行列で、
単位行列(unit matrix)もしくは恒等行列(identity matrix)と呼ばれ、
I と表されることが多い。
対称行列の定義のところでは、それが実行列であるか複素行列であるか
を問題にしなかった。もちろん複素行列でも対称行列は可能なのだが、
実対称行列にはもう1つの複素領域への拡張の方法があり、理論的には
こちらの方が重要である。さて一般に n 次の複素行列 C を考え
てみよう。その第 j 行 k 列要素 cjk は、それが複素数であることを明示すれば、
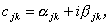
| (A.12) |
と書ける。ここで、αjk 及び βjk は、複素数 cjk の 実部(real part)及び虚部(imaginary part)であり、 共に実数である。もちろん、i 2 = -1 である。この時、cjk の 共役複素数(complex conjugate number)は、

| (A.13) |
と書ける。
つぎに、(A.13) 式で、定義される 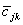 を要素とする行列を
を要素とする行列を
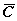 と書くことにする。すなわち、
と書くことにする。すなわち、
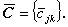
| (A.14) |
この時、
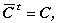
| (A.15) |
なる性質をもつ行列は、エルミート行列(Hermitian matrix)と呼ばれる。
(A.15) 式を言葉で表現すると、エルミート行列とは、(正方複素)行列の共役複素数を要素とする行列の転置行列が
もとの行列に等しい行列である、ということになる。 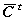 は、
行列 C の共役転置(conjugate transpose)と呼ばれる。
行列 C の共役転置行列
は、
行列 C の共役転置(conjugate transpose)と呼ばれる。
行列 C の共役転置行列 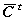 は、しばしば C*
と書かれる。
は、しばしば C*
と書かれる。
エルミート行列は、もしその要素がすべて実数、すなわち実行列とすれば、対称行列
に等しい。なぜならば、実数の共役複素数は、もとの実数そのものであるから。
(A.1)式の行列 A で、m = 1 のケース及び n = 1 のケース、すなわち

| (A.16) |
及び
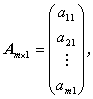
| (A.17) |
は、ベクトル(vector)と呼ばれることもある。(A.16)式のベクトルは行ベクトル(row vector)、(A.17)式のベクトルは列ベクトル(column vector)と呼ばれる。このようにベクトルは行列の特別なケースにあたるが、ベクトルであることを明示する場合には大文字でなく小文字で
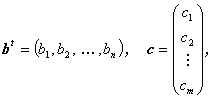
| (A.18) |
のように表記することが多い。
ベクトルの各要素が、多次元空間の座標値を表す場合には、そのベクトルは位置ベクトル(position vector)と呼ばれる。行列の定義からは、任意のベクトルは必ずしも位置ベクトルである必要はない。
スカラー(scalar)量に加減乗除が定義されるように、行列同志の加減乗除の定義も 可能である。一般に、m 行 n 列の行列を A = { ajk } , B = { bjk } とする時、まず加算減算は
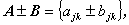
| (A.19) |
のように定義される。すなわち、それらは m 行 n 列の2つの行列の対応する要素の和(差)を取ることと定義される。より正確には、減算(差)は加算より
定義される。
3つ以上の行列の加算減算については、その順序は問題にならない。すなわち、
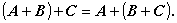
| (A.20) |
ここで、もちろん C も、m 行 n 列でなければならない。
2つの行列の積については、加算減算の場合と異なり、掛けるべき2つの
行列 A 、B それぞれの行数・列数につぎの制約が必要となる。ここで、C は、A と B の掛算の結果得られる行列とする:
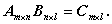
| (A.21) |
すなわち、(A.21)式で明示した各行列の型から、掛算の左側の行列の列数(この場合
n)と、同右側の行列の行数は同じでなければならない。この制約からただちにわかることは、行列の掛算では
一般には A B は定義できても B A は必ずしも定義できないことがあり得る、
ということである。
(A.21)式は、行列の掛算における各行列の型すなわち行数及び列数の制約について述
べているのみである。実際の掛算では、行列の要素をつぎのように計算しなければな
らない。ここで cjk はもちろん、行列 C の第 j 行 k 列の要素の値とする:
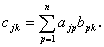
| (A.22) |
(A.21)式の行列の積の特別の場合の1つは、行列のべき乗(power of a matrix)を定義する。たとえば、(A.21)式で B が A と同じ型すなわち m 行 n 列の矩形行列であり、かつ A に等しいとする。この時、
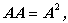
| (A.23) |
と書く。これを p 回繰り返せば、 Ap が定義できる。Ap は、 行列 A の p 乗(p-th power of A)と呼ばれる。通常 p は整数である (ここまでのところでは、正の整数まで)が、行列 A が対角行列の場合、
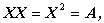
| (A.24) |
となる行列 X のことを、A1/2 と書く。 行列 A が(A.11)式なる対角行列ならば、
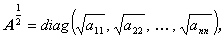
| (A.25) |
と書ける。
より一般的には、任意の正方行列 A が正の半定符号ならば、
その平方根A0=A1/2 が存在する。
(A.21)式及び(A.22)式の定義から、AB も BA も共に定義できるためには、
この式での行列 B の型は n 行m 列でなければならないことがわかる。
この時、さらに(A.22)式より、一般に
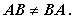
| (A.26) |
すなわち、行列の積演算では、一般に交換律が成り立たないことが明らかである。
行列の差が行列の和を用いて定義できるように、行列の除算すなわち行列の逆行列(inverse matrix)の定義は、(A.21)式の行列の乗算(積)を用いて定義できる。通常行列の逆行列は、正方行列の場合にのみ定義され、つぎのようになる。すなわち、任意 の正方行列 A の逆行列 X は、
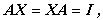
| (A.27) |
なる X を満たす行列で、もしそのような X が存在するとき、 それをA -1 と表す。ここで、I は、単位行列である。 (A.27)式の逆行列の定義は、スカラー量aの逆数の定義
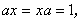
| (A.28) |
を一般化したものになっていることがわかる。
(A.27)式の定義は、行列の逆行列の形式的な定義であり、代数的な定義は、
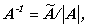
| (A.29) |
で与えられる。ここで、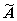 は行列 A の
余因子行列(adjoint of A)、
|A | は行列 A の行列式
(determinant) である。行列式については、後で定義する。実際の逆行列の計算は、
数値解法が確立されており、(A.29)式を用いることはまずない。
は行列 A の
余因子行列(adjoint of A)、
|A | は行列 A の行列式
(determinant) である。行列式については、後で定義する。実際の逆行列の計算は、
数値解法が確立されており、(A.29)式を用いることはまずない。
(A.29)式から明らかなように、正方行列の逆行列は行列式の値がゼロの場合
計算できない。
一般に、逆行列がある種の特別な形をしている行列で、基本的に重要なものが2つあ
る。それらは、直交行列(orthogonal matrix)と
ユニタリ行列 (unitary matrix) である。
直交行列とは、
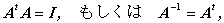
| (A.30) |
なる実正方行列のことをいう。
一方、ユニタリ行列とは、
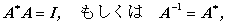
| (A.31) |
なる複素正方行列のことをいう。これら2つの定義から、直交行列はユニタリ行列の 特別なケースとなっていることが容易にわかる。
前節では、行列同志の加減乗除演算の定義について述べた。これらの定義及び数( number)の定義から、つぎのような行列とスカラーとの積に関する演算法則が導かれる:
|
ここで、α ,β は実数もしくは複素数であるとする。
ここで、上の演算法則を用いると、われわれは、本書の後半で最も重要なエルミー
ト行列を定義できる。すなわち、
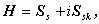
| (A.32) |
ここで、行列 H の共役複素行列 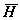 は、共役複素数の定義から、
は、共役複素数の定義から、
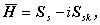
| (A.33) |
と書ける。ここでさらに、行列 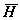 の転置行列
の転置行列 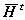 を作ると、転置行列の性質等から、
を作ると、転置行列の性質等から、
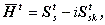
| (A.34) |
が導かれる。ここで、
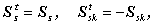
| (A.35) |
に注意すると、
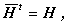
| (A.36) |
すなわち、行列 H は、(A.15)式を満たすので、エルミート行列であることがわかる。
前節の逆行列の定義のところで、任意の正方行列の行列式及び余因子行列の 概念を述べたが、そこではそれらの定義はしなかった。ここでは、それらの 定義を行う。よく知られているように、行列式の起源は連立一次方程式の 解法にあるわけであるが、ここではそれにはふれず、定義のみ述べる。一般に 任意の n 次の正方行列
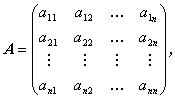
| (A.37) |
の行列式を |A | と表すとすると、それは行列 A の 任意の行、例えば第 j 行要素の言葉で
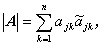
| (A.38) |
とするか、もしくは同行列の任意の列、例えば第 k 列要素の言葉で
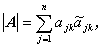
| (A.39) |
とするか、のいずれでも表される。ここで、これらの式における 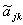 は、
ajk の余因子 (cofactor) と呼ばれ、
は、
ajk の余因子 (cofactor) と呼ばれ、

| (A.40) |
と書ける。ここで、(A.40) 式の Djk はもとの行列 A の第 j 行と第 k 列のすべての
要素を除いてできる n -1 次の行列の行列式である。
逆行列のところで出てきた余因子行列 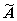 は、(A.40) 式を
使ってつぎのように定義される:
は、(A.40) 式を
使ってつぎのように定義される:
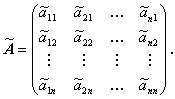
| (A.41) |
まず、つぎの2次の行列 A 2 の行列式を計算してみよう:
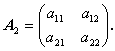
| (A.42) |
ここで、A 2 の例えば第1列要素 a11 ,a21 を用いて これを表現すると、定義より
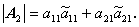
| (A.43) |
ここで余因子の定義から
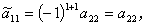
| (A.44) |
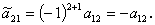
| (A.45) |
したがって、
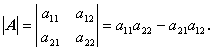
| (A.46) |
つぎに、3次の行列 A 3 の場合、
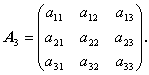
| (A.47) |
今度は、この行列の例えば第2行要素 a21 ,a22 ,a23 を使って、 この行列式を計算してみよう。この時、定義より
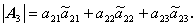
| (A.48) |
ここで、余因子の定義及び (A.46) 式で与えられる2次の行列式に注意すると、
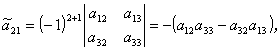
| (A.49) |
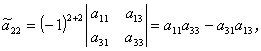
| (A.50) |
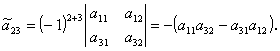
| (A.51) |
これらより、
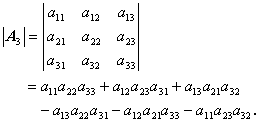
| (A.52) |
(A.29) 式から明らかなように、正方行列 A は、その行列式がゼロの場合、(通常の意味での) 逆行列が定義できない。逆行列が定義できる行列は、正則行列 又は 非特異行列 (nonsingular matrix) と呼ばれる。 一方、行列式がゼロの行列は 非正則行列又は 特異行列 (singular matrix) と呼ばれる。 正方行列が非正則の場合やより一般の m ×n 型行列の場合に逆行列の概念を拡張することも可能であり、 そのように拡張された逆行列を一般化逆行列(generalized inverse) と呼ぶ。 一般に、AXA = A を満たす行列 X をm ×n 型行列 A の一般化逆行列と呼び、X = A - と書く。
まず、集合 V と体 (field) F を仮定しよう。 この時、集合 V は、つぎの公理を満たす時、ベクトル空間 (vector space) と呼ばれる:
|
もし、上の定義で、体 F が実数であればベクトル空間 V は、実ベクトル空間 (real vector space)、複素数ならば複素ベクトル空間 (complex vector space) と呼ばれる。
上の定義は、非常に抽象的な定義であり、通常のベクトル以外の集合も含む。
例えば、m 行 n 列の(複素)行列の集合も、行列の加法と乗法に関してベクトル空間をなす。また、体 F が非可換 (non-commutative) の場合には、左ベクトル空間 (left-handed vector space) と右ベクトル空間
(right-handed vector space) を区別するので、うえの定義はそのような場合には、
厳密には左ベクトル空間と呼ばれる。ただし、以下の議論では可換な数体のみを扱う
ので、この区別はしない。ここで、可換・非可換の違いは、体の公理のうち乗法の交換法則
(commutative law) が成立するかどうかによる。
すなわち、a ,b を体 F の元として、ab =ba が成り立つような体を可換体、
成り立たないような体を非可換体という。
まず、ベクトル空間上の p 個のベクトルの一次従属性について述べる。そのために、
最初にベクトルの一次結合 (linear combination) を定義する。
体 F 上のベクトル空間V のベクトルv1,v2,
... ,vpに対して、
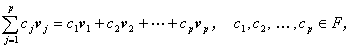
| (A.53) |
なるベクトルを、v1,v2, ... ,vp
の一次結合という。
ベクトル空間上のp 個のベクトル {v1,v2,
... ,vp } は、もし
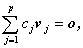
| (A.54) |
を満たす少なくとも1つはゼロでないような c1,c2,
... ,cp が存在する時、一次従属 (linearly dependent)
であるという。
言い換えれば、ベクトルv1,v2, ...
,vp は、それらのうち少なくとも1つが他のベクトルの一次結合で表されるならば、
一次従属である、という。
これに対して、ベクトルv1,v2,
... ,vp が一次従属でない時、
一次独立 (linearly independent) であるという。
つぎに、ベクトル空間 V で、p を適当な自然数として、p 個より多い一次独立なベクトルが
存在しない時、V は有限次元 (finite dimensional) という。
この時、V に含まれる一次独立なベクトルの最大数を V の 次元
(dimension) といい、dim (V ) で表す。dim (V ) が無限の時、V は
無限次元 (infinite dimensional) と呼ばれる。
ベクトル空間 V の次元が p の時、V 中の一次独立な p 個のベクトル組
b1,b2, ... ,bp を V の
基 (basis) という。
例えば、p 次元実ベクトル空間上のp 個のベクトル
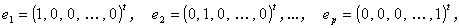
|
は、1つの基を構成する。特に、この基は標準基 (standard basis) と呼ばれる。
最後に、ベクトル空間上のノルムの定義を行う。
ベクトル空間 V 上のノルム (norm) とは、V 上で定義される実数値関数で、
その値は ||v || と表記され、すべての u ,v ∈V に対して
つぎの3つの公理を満たす:
|
一般に、複素ベクトル空間 C p は、任意の2つのベクトル u ,v ∈C p に対して、u とv の 内積 (inner product)
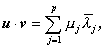
|
が定義できる時、内積空間 (inner product space) と呼ばれる。ここで、
u = ( λ1,λ2, ... ,λp )
t ,
v = ( μ1,μ2, ... ,μN )
t とする。 は、λj の共役複素数である。
は、λj の共役複素数である。
内積空間における操作
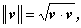
|
は、任意の非ゼロベクトル v に対して、正の実数を割り当てる操作であり、
ベクトルの長さ (length of a vector) を定義する。
ベクトルの長さ ||v || は、ノルムの一例であり、その意味で
内積空間はノルム化された空間 (normed space) と言える。
前節ではベクトル空間の定義を行ったが、そこでの構成要素はベクトルの集合
と体を成すスカラーの集合の2種類であった。
これに対して、線型空間 (linear space) は、
これら2種類の集合にさらに「点」と呼ばれる元 A,B,C, ... から成る集合 L を持つ
特別な空間である。
一般に、何らかの可換体 K 上のベクトル空間 V に、点の集合
L ( A,B,C, ...) が与えられ、つぎの公理を満たす時、
L は体 K 上の線型空間もしくはアフィン空間 (affine space) と呼ばれる:
|
線型空間 L に付属するベクトル空間 V の次元は、L の次元と呼ばれ、
dim (L ) で表される。
O を p 次元線型空間 L p 上で任意に固定された点とする。
この時、 L p に付属するベクトル空間 V p の1組の
基 ( b1,b2, ... ,bp ) を用いると、
われわれは
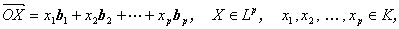
| (A.55) |
により、L p 上の点 X と p 個の K の元の
組 ( x 1,x 2, ... ,xp )
とを一対一に対応させることができる。
この時、1点 O ∈L p と
基 ( b1,b2, ... ,
bp ) の組
S ( O ; b1,b2,
... ,bp ) を座標系
(coordinate system)、点 O をその原点
(origin)、K の元の組
( x 1,x 2, ... ,xp )
を座標系 S に関する点 X の座標 (coordinate)
と呼ぶ。
L 1 ,L 2 を体 K 上の線型空間とする。 変換 T : L 1→ L 2 は、 つぎの関係を満たす時、一次変換もしくは線型変換 (linear transformation) と呼ばれる。 すなわち、任意の x 1 ,x 2 ∈ L 1 及び任意のスカラーc ∈K に対して、
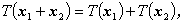
| (A.56) |
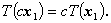
| (A.57) |
(A.56) 式及び (A.57) 式は、T がそれぞれ
加法的 (additive) 及び
斉次 (homogeneous) であることを示す。
例えば、2次元空間で位置ベクトル
x = (x 1 ,x 2)t
に対するつぎの変換
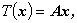
| (A.58) |
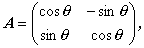
| (A.59) |
は、明らかに (A.56) 式及び (A.57) 式を満たすので、一次変換である。
これにより生成されるベクトルを x ’とすると、
x ’は x をその平面上で反時計廻りに
θ だけ回転したものになる。
また、例えば n 次元空間の位置ベクトル x に対する
m 行n 列行列 A を用いたつぎの変換
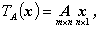
| (A.60) |
は、n 次元ベクトル x を m 次元ベクトルに変換する
一次変換である。
とりわけ、A が正方行列でありかつ直交行列の場合、
(A.60) 式の行列 A の行列式は 1 又は -1 であり、
対応する一次変換はそれぞれ正回転、負回転であるという。
任意のm 行n 列の行列 A は、 その前や後からある種の行列を掛ける操作により、幾つかの基本的な形に帰着でき、 それらは行列の基本特性の1つを示す。 これらの操作は、 行列の基本操作 (elementary operation) と呼ばれ、 つぎの3つからなる:
|
これらの操作を行うための行列は簡単で特別な形をしているが、 ここでは本書の内容に直接関係しないので、省略する。 いずれにせよ、これらの基本操作により、任意の行列 A は、 つぎのいずれかの 正準形 (canonical form) に帰着されることがわかっている:
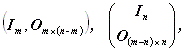
| |
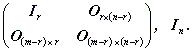
|
ここで、うえの幾つかの単位行列の右下の添字は、単位行列の次数を表す。
また、r は 1 ≦ r ≦ min (m ,n ) である。
上の正準形における単位行列の次数は、
行列 A の階数 (rank) と呼ばれる。
例えば、n 次の行列 A の階数は、A が正則の時に限り、
n である。
一般に、n 次の正方行列 A は、A.1.6 節の視点からは、 n 次元線型空間 V n 上の一次変換とみれる。 ベクトル x ∈V n に対する 一次変換が つぎの関係を満たす時、
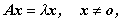
| (A.61) |
x は、
固有値 (eigenvalue) λ に対する
A の固有ベクトル (eigenvector) と呼ばれる。
ここで、A の要素は、実数であろうが複素数であろうがかまわない。
(A.61) 式は、
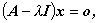
| (A.62) |
の形に書け、 この式が自明でない解 (non-trivial solution) を持つためには、 A -λI の行列式、すなわち
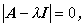
| (A.63) |
でなければならない。
(A.63) 式をスカラー表現すると、

| (A.64) |
の形に書ける。(A.64) 式は行列 A の
特性方程式又は
固有方程式(characteristic equation) と呼ばれる。
(A.64) 式から、行列 A の固有値は n 次方程式の根となっている
ことがわかる。
一般に、正方行列 A が与えられた時、(A.61) 式を満たす固有値と、
対応する固有ベクトルを求める問題は、
固有値問題 (eigenvalue problem) と呼ばれる。
(A.64) 式は、n 次方程式であり、よく知られた
アーベルの定理 (Abel's theorem) により、
5次以上の場合、代数的には(累乗根によっては)解けない(例えば、奥川、1966)が、
数値解析的には多くの方法が開発されており、固有値問題というタイトルのついた本が
幾つか出版されている(例えば、Wilkinson, 1965)。
一方、固有ベクトルの方は、固有値が求められると (A.62) 式の関係を用いて
求めることができる。ただし、一般に固有ベクトルは、その長さを変えても
(A.61) 式を満たすので、長さに関する不定性のみは避けられない。したがって、
固有ベクトルはある長さを定めて求める。
これらの詳細については、Wilkinson (1965) などを参照されたい。ここでは
つぎに、本書にかかわる固有値問題の初等的知識(定理)を幾つか列挙する
に止める。
|
本書で中心的役割を果す非対称(非)類似度行列は、
(A.37) 式の形の正方行列 A である。
したがって、A が一次変換により、
どのような形に変換できるのかを見ておくことは重要である。
行列の分野では、
ジョルダンの標準形 (Jordan canonical form)、
フロベニウスの標準形 (Frobenius canonical form)、
三角標準形 (triangular canonical form)、
スミスの標準形 (Smith's canonical form)、
実標準形(real canonical form) などが、
よく知られている。
これら5つの標準形のうち、スミスの標準形を除いては、すべて相似変換により達成される。
一方、スミスの標準形は、
等積変換 (equivalence transformation、
すなわち P A Q の形の変換)という
より広い変換により達成される標準形なので、ここでは省略する。
以下の A はすべてn 次である。
定理1(ジョルダンの標準形)
A の固有値は
λ1,λ2, ... ,λr で、
それぞれの重複度 (multiplicity ) は
m1,m2, ... ,mr とする。
この時、A は相似変換により、つぎのジョルダンの標準形に帰着される:
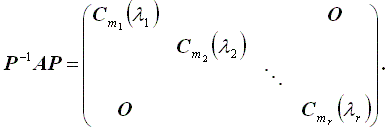
| (A.67) |
ここで、Cmi (λi ), i = 1,2, ... ,r は、 mi 次の行列で、
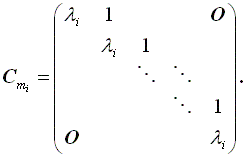
| (A.68) |
定理2(フロベニウスの標準形)
A は、相似変換により、s 個のフロベニウス行列
Br1,Br2, ... ,
Brs の
直和 (direct sum) に変換できる:
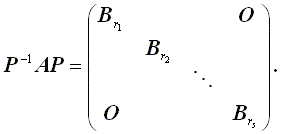
| (A.69) |
ここで、フロベニウス行列 Br は
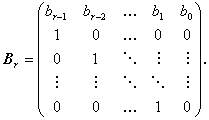
| (A.70) |
定理3(三角標準形)
A は相似変換により、
三角行列(上側三角もしくは下側三角)に帰着できる。
定理4(実標準形)
A は相似変換により、本文の (2.137) 式の実標準形に帰着できる。
n 次の正方行列を A 、2つのn 次ベクトルを x ,y ∈V n とする。この時、
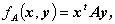
| (A.71) |
は、双一次形式 (bilinear form) と呼ばれる。 双一次形式は、その定義から明らかなように、スカラーである。 (A.71) 式の行列 A は 生成行列(generating matrix) と呼ばれる。
n 次の実対称行列 A 及び n 次ベクトル x ∈V n から作られるつぎの形式
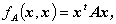
| (A.72) |
は、双一次形式の特別なもので、 二次形式 (quadratic form) と呼ばれる。 二次形式も双一次形式と同様スカラーであり、その符号に応じてつぎのように呼ばれる:

|
ここで、うえの4つは、順に
正(定)値、
負(定)値、
非負(定)値、
非正(定)値、とも呼ばれる。
また、非負の定符号及び 非正の定符号は、
それぞれ正の半定符号 (positive semi-definite) 及び
負の半定符号 (negative semi-definite) とも呼ばれる。
もし、二次形式の符号がうえのいずれにも属さぬ、すなわち正にも負にもなる時、
不定符号 (indefinite) と呼ばれる。
さらに、二次形式の生成行列 A は、二次形式の符号が、正、負、非負、非正、に応じて、
正の定符号又は正(定)値、負の定符号又は負(定)値、
非負の定符号又は非負(定)値、非正の定符号又は非正(定)値、と呼ばれる。
生成行列 A がこれらのいずれにも属さぬ時、不定符号と呼ばれる。
n 次の実対称行列 A 及びn 次の実ベクトル x から二次形式が作られるのと同様にして、 n 次のエルミート行列 H 及びn 次の複素ベクトル z から作られる形式
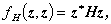
| (A.73) |
は、エルミート形式 (Hermitian form) と呼ばれる。 ここで、ベクトル z * は、 ベクトル z の共役転置すなわち、
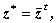
| (A.74) |
であり、z = ( z 1,z 2, ... ,zn ) t とすると、
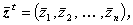
| (A.75) |
と書ける。ここで、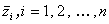 はもちろん
zi の共役複素数である。
はもちろん
zi の共役複素数である。
エルミート形式の文脈では、(A.73) 式の「*」すなわち共役転置の記号は、
「H 」と書かれることもある (例えば、Wilkinson, 1965)。
エルミート形式は、(A.73) 式から明らかなように、その構成要素が
z も H も共に複素数から成るにもかかわらず、(A.15) 式の
エルミート行列の性質に注意すると、
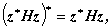
| (A.76) |
が成り立つので、実数(のスカラー)である。
さらに、定義から明らかなように、エルミート形式は二次形式の拡張になっている。
エルミート形式はその値が実数であるので、二次形式と同様その符号の正負を議論できる。
すなわち、

|
もし、エルミート形式の符号がうえのいずれにも属さぬ、すなわち正にも負にもなる時、
不定符号と呼ばれる。
さらに、エルミート形式の生成行列 H は、
エルミート形式の符号が、正、負、非負、非正、に応じて、
正の定符号又は正(定)値、負の定符号又は負(定)値、
非負の定符号又は非負(定)値又は正の半定符号、
非正の定符号又は非正(定)値又は負の半定符号、と呼ばれる。
生成行列 H がこれらのいずれにも属さぬ時、不定符号と呼ばれる。
エルミート形式は、本書第5章で述べるように、非対称MDSの非距離
モデルを統一的に解釈するために筆者らが開発した新たな非対称MDS HFM の
数学的基礎を与える。
A.1.8 節で述べた固有値問題と深い係わりを持つのが、ここで述べる
特異値分解 (singular value decomposition) である。
固有値問題、したがって固有値分解
(eigenvalue-eigenvector decomposition) が、n 次の正方行列 A
を対象とするのに対して、特異値分解は一般の矩形行列すなわち
m 行n 列から成る行列 A を対象とする。
まず、わかりやすいように、実数を要素とする矩形行列から始めよう:
定理5(特異値分解)
行列 A を階数 r の m 行n 列の行列とする。
この時、m 行m 列の直交行列 U 、
n 行n 列の直交行列 V 、
及び m 行n 列の(広義の)対角行列 S で、
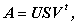
| (A.77) |
なる関係を満たすものが存在する。ここで、S の対角要素は非負で、
大きさの順に並べられ、それらのうちのr 個は正である。
特異値分解は、複素行列についても成り立つ。この場合、
定理1の直交行列 U,V はユニタリ行列に、
(A.77) 式の V の転置行列 V t
を共役転置 V * に、置き換えれば良い。
一般に、任意の行列 A の特異値分解は、
2つの行列 A ,A * 及び
A *,A の固有値問題を解くことにより得られる。
テンソルの第1歩は 1-形式 (1- form)
と呼ばれるもので、ベクトル空間 V 上の
線形実数値関数 (real-valued function) として定義される。
すなわち、1-形式はベクトルを実数値に変換する一つの関数である。
一方、p-形式 ( p - form) とは、
ベクトル空間 V 上の p 個のベクトルの線形実数値関数で、
p 一次 (p-linear) で
反対称な(antisymmetric) 性質を持つものとして定義される。
よく知られた p -形式の1つは、向きづけられたユークリッド空間上での
平行体 (parallelotope) の向きづけられた体積である。
1-形式や p -形式をさらに一般化したのが
テンソル (tensor) である。
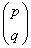 型テンソルとは、
p 個の1-形式と q 個のベクトルを変数とする
多重線形実数値関数として定義される。
型テンソルとは、
p 個の1-形式と q 個のベクトルを変数とする
多重線形実数値関数として定義される。
例えば、通常のスカラーは 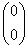 型テンソル、
ベクトルは
型テンソル、
ベクトルは  型テンソル、
1-形式は
型テンソル、
1-形式は 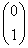 型テンソル、
面積は
型テンソル、
面積は 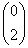 型テンソルである。
内積も面積と同じく
型テンソルである。
内積も面積と同じく 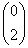 型テンソルであるが、
計量テンソル(metric tensor) と呼ばれることもある。
型テンソルであるが、
計量テンソル(metric tensor) と呼ばれることもある。
複素数 (complex number) z とは、 任意の実数 x 、y 及び i 2 = -1 なる i を用いて、 一般に
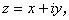
| (A.78) |
と表される。(A.78) 式の右辺の x 及び y は、
それぞれ複素数の実部(real part) 及び
虚部 (imaginary part) と呼ばれる。
これらは、Re z 及び Im z と書くことがある。
複素数は、一般にその実部を x 軸(実軸)座標、
虚部を y 軸(虚軸)座標とする複素平面上の点として表すことも出来る。
この意味では、複素平面(1次元複素空間) C は
2次元実空間 R 2 と同一視できる。
複素数 z は、しばしば極座標 (polar coordinates)
を用いて表現される。ここで、
複素平面上の実軸から点z までの反時計廻りで測った角度をθ ラジアンとすると、z は
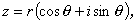
| (A.79) |
なる極形式 (polar form) にも書ける。もちろん、この時、
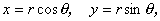
| (A.80) |
である。
一般に、複素数 z の原点からの長さを |z | と書くと、
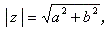
| (A.81) |
である。|z | は、z の絶対値もしくは
モジュラス (modulus)と呼ばれる。
つぎに、2つの複素数
z 1 ( = x 1 + i y 1 )
及び z 2 ( = x 2 + i y 2 ) の積は、
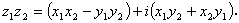
| (A.82) |
これを極形式を用いて書くと、
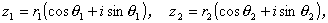
|
とすれば、
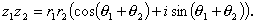
| (A.83) |
同様に、

| (A.84) |
一般に、A.12.1 で定義された複素数 z ∈C を要素として持つ 複素ベクトル (complex vector) u ∈C p
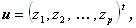
| (A.85) |
を考える時、その集合 V と体 F を仮定したとして、 V 上に A.5.1 節で述べた加法とスカラー乗法が定義出来る場合、 そのような空間は複素ベクトル空間と呼ばれることは、A.5.1 節で述べた通りである。
もしわれわれが、前節で述べた複素ベクトル空間 V 上の任意の2つのベクトル x 、y に対して、 本文 5.1.2 節で定義したエルミート形式の3つの特性 (i) 、(ii) 、(iii) を満たすような関数 φ ( x ,y ) を定義でき、 さらに φ ( x ,y ) は 任意の x ≠ o に対して正の時、 φ ( x ,y ) は(エルミート)内積と呼ばれる。 この場合、われわれは複素ベクトル空間上にノルム
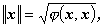
| (A.86) |
を定義できる。
このように(エルミート)内積が定義出来る空間は、
前ヒルベルト空間 (pre-Hilbert space) と呼ばれる。
一般に、前ヒルベルト空間では次の極恒等式 が成り立つ:
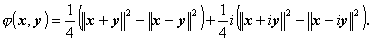
| (A.87) |
もし、V が実前ヒルベルト空間 (real pre-Hilbert space) ならば、(A.87) 式は
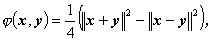
| (A.88) |
と書ける。ここで、ユークリッド空間では内積は、 x t y と書けることに注意しよう。 実は、(A.88) 式はユークリッド空間の場合、変形すると
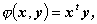
| (A.89) |
と書ける。つまり、ユークリッド空間は前ヒルベルト空間の特別な場合であると言える。
前ヒルベルト空間は完備 (complete) であれば、
ヒルベルト空間と呼ばれる。一般に、ヒルベルト空間は必ずしも有限次元である必要はないが、
有限次元空間は完備であるので、本書のエルミート形式モデルで扱う有限次元空間は、
(複素)ヒルベルト空間である、と言える。
量子物理学 (quantum physics) においては、
その数学的骨組みは(無限次元)複素ヒルベルト空間上の
線形作用素 (linear operator) の理論により与えられるが
(例えば、Blank, Exrer, & Havlicek, 1994) 、
計量心理学の分野では、2.1.1 節で述べた lp ノルムまでしか
現在までのところ本邦においても欧米においても知られておらず、
非対称 MDS における複素ヒルベルト空間の導入は、
Chino and Shiraiwa (1993) が最初である。