第1章 微積分入門のホームページへようこそ
![]()
![]()
この頁は、平成16年7月22日に新たに開設しました。
この頁は、令和2年5月18日に一部更新しました。
以下の議論のため、集合 (set) の概念について、まず簡単にふれ る。一般に集合とは、何らかの共通特性を持つ物の集まり (a collection or family of things) で ある。物は数字とは限らず、例えば世界の自動車メーカーでもよいし、地球上の生物でもよい。集合 に属する物は、集合の要素あるいは元 (elements, or members) と呼ばれる。
一方、要素が存在しない集合は、空集合 (the empty set) あるいは 零集合 (the null set) と呼ばれ、φ と書かれる。また、要 素が1つしかない集合は 単集合 (singleton) と呼ばれる。
つぎに、2つの集合 A と B があるとき、もし B のすべての要素が A の要素でもある場合、B は A の 部分集合 (a subset) と呼ばれ、通常 B ⊂ A と書かれる。例えば、 整数の集合を I、実数の集合を R と書けば、I ⊂ R である。もし B ⊂ A でありかつ A ⊂ B ならば、 2つの集合は等しく A = B と書く。また、もし A と B が等しくない場合、A の 空でない (a nonempty) 部分集合 B は、真部分集合 (a proper subset) と呼ばれる。
最後に、2つの集合 A と B のどちらかに含まれるすべての要素から成る集合は、 和集合 (the union of the sets) と呼ばれ、A ∪ B と書かれる。これは、 A ∪ B ≡ { a| a⊆ A or a ⊆ B } のように表記できる。一方、2つの集合 A、B に対して、 それらの両方に含まれる要素から成る集合は、共通集合 (the intersection of the sets) と呼ばれ、A ∩ B ≡ { a| a⊆ A and a⊆ B } のように表記できる。
すべての数を S、T の二組の集合に分けて、S に属する各数を T に属する各数よりも小さくすることができ たとするとき、このような組み分け (S,T) を デデキントの切断 (Dedekind's cut) といい、S を下組、T を上組という。
実数集合 R の空でない部分集合 S、T による任意の切断 ( S , T ) に対して、ある x ⊆ R が存在して、すべての s ⊆ S は s ≦ x であり、すべての t⊆ T は t≧ x となるような x は唯一つ存在する。
この公理は、デデキントの連続性公理 (Dedekind's axiom of continuity) と呼ばれる。
(註1) 切断は理論上つぎの三つの型が可能である。
|
集合 S に属する数がすべて一つの数 M よりも大(あるいは小)でない時には、S は 上方に有界 (bounded downwards) 、あるいは 下方に有界 (bounded upwards) といい、M をその一つの上界 (an upper bound) あるいは1つの下界(a lower bound) という。 また、上方にも下方にも有界ならば、単に有界(bounded) という。
|
集合 S の上限 (supremum、略して sup.)a とは、つぎの2つを満 たす数である:
|
下限 (infimum、略して inf.)については、不等号の向きを変えればよい。
|
数の集合 S が上方または下方に有界ならば、S の上限または下限が存在する。
[ 演習 1.1 ] 定理1を証明せよ。
a1, a2, ..., an のように無数の数を一定の順序に並べたものを 数列 (sequence) という。ここで、n は 自然数 (natural number) であり、an は変数 n の関数である。この関数が確定したとき、 数列を { an } と書く。
n を限りなく大きくするとき、an がある決まった値 c に限りなく近づくならば、
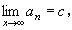
| (1.1) |
と書く。また、このとき数列 { an } は c に収束する (converge) するといい、c を { an } の極限 (limit) という。
an → c ならば、|an|< M なる定数 M が存在する。また、| c | ≦ M .
[ 演習 1.2 ] 定理2を証明せよ。
数列 { an } が、a1 < a2 < ... < an < ... のように、 各項がその番号と共に増大するとき、数列は単調に増大するという。一方、不等号を逆にした場合は、 数列は単調に減少するという。単調に増大または減少する数列は、 単調数列 (monotone sequence) という。
[ 演習 1.3 ] 定理3を証明せよ
一つの集合 S について、ある点 A が集積点であるとは、点 A にどれだけ近いところにも S に 属する点があることをいう。ただし、A は必ずしも S に属する点でなくてよい。
[ 演習 1.4 ] 定理4を証明せよ
[ 演習 1.5 ] 定理5を証明せよ
点集合 S のすべての集積点が S に属するとき、S は閉集合 (closed set) という。
f ( x ) を x の関数とし、x = a では f ( x ) は必ずしも定義されていないものとする。 x を a に限りなく近づけるとき、f ( x ) がある決まった値 c に限りなく近づくとき、これを
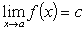
| (1.2) |
と書き、c を x が a に近づいたときの f ( x ) の極限 (limit) という。
より正確な極限の定義は、つぎのようである: 定義10(関数の極限)
limx→ af ( x ) = c とは、どんな正数 ε を任意に与えても、ある適当な正数 δ をとり、 | x - a | < δ のようなすべての x について、| f ( x ) - c | < ε とすることができることである。
関数の極限の記号を用いると、f ( x ) の微分係数をつぎのように定義できる。
f ( x ) に対して
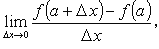
| (1.3) |
が存在すれば、x = a における関数 f ( x ) の x についての微(分)係数 (differential coefficient) という。なお、このとき x = a で関数 f (x) は可微分 (differentiable) であるという。
ここで、(1.2) 式における a をいろいろ変えると、微(分)係数はその関数となる。 このことから、微(分)係数はそれを取る場所の関数と考えるとき、もとの関数の 導関数(derivative) という。すなわち、f ( x ) の導関数 f '( x ) は、 つぎのように書ける:
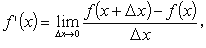
| (1.4) |
関数 f ( x ) が x = a において連続 (continuous) であるとは、 limx→ af ( x ) が存在し、かつこれが f ( a ) に等しいことをいう。また、 f ( x ) が x のある区間において連続 であるというのは、この区間内 の各点で f ( x ) が連続であることをいう。
| (註) 一般に、x = a で f ( x ) が可微分ならば、x は a で連続であるが、その逆は必ずしも成り立 たない。 |
関数 f ( x ) が a≦ x ≦ b で連続ならば、任意の正数 ε を与えたとき、これに応じて適当な幅 δ をとれば、 この区間のどの場所にでも、距離が δより小すなわち | ξ 1 - ξ 2 | <δ なる二点を とれば必ず| f ( ξ 1 ) - f ( ξ 2 ) | < ε とすることができる。
これは連続関数の一様連続性 (uniform continuity) といわれる。
[ 演習 1.6 ] 定理6を証明せよ。
ある区間 I で連続な関数 f ( x ) が、この区間内の点 a、b で相異なる値 f ( a ) = α、 f ( b ) = β を取るとする。この時、α、β の中間の任意の値 を μ とすれば、

| (1.5) |
なる点 ξ が存在する。
[ 演習 1.7 ] 定理7を証明せよ。
(註1)Atkinson (1978, pp.3-4) では、高木の紹介する中間値の定理と少し異なる定義がなされている。すなわち、
(一般には、複素値)関数 f ( x ) が limx → a f ( x ) = ∞ または limx→a f ( x ) = 0 の場合、それぞれ f を a における無限大 (infinity)、または 無限小 (infinitesimal) という。
|
f、g が共に無限大か、共に無限小の場合、
|
ここで、O, o は、ドイツ語の Ordnung (英語 order) の頭文字で、Landau の記号 (Landau's symbol) という。
|
[ 演習 1.8 ] 上の無限小についての各性質を、関数の極限の定義10を用いて 証明せよ。
うえの無限小についての性質を用いると、つぎの極限演算の法則を導くことができる。ここで、 limx→af ( x ) = p、limx→ag ( x ) = q とする:
|
[ 演習 1.9 ] 上の極限演算の4つの法則を証明せよ。(ヒント:関数の極限 (1.2) 式は、無限小 η を用いて f ( x ) = c + η とも書けることに注意)
うえの極限演算の法則を用いると、つぎの微分演算の法則を導くことができる
微分演算の法則
|
[ 演習 1.10 ] 上の9つの微分演算の法則を証明せよ。
うえの極限演算の法則は、導関数を用いた表現であるが、微分の形で表すと つぎのように書ける:
|
ここでは、まず基本的な微分に関する公式を列挙する:
|
|
[ 演習 1.11 ] 上の最初の微分公式を証明せよ。
以下に、微分に関する幾つかの基礎定理をあげる。
関数 f ( x ) が区間 a≦ x ≦ b で連続、a < x < b で可微分、f ( a ) = f ( b ) ならば、a < x < b の 範囲のある点 ξ において必ず f '( x ) = 0 となる。
[ 演習 1.12 ] ロルの定理を証明せよ。
関数 f ( x ) が区間 a ≦ x ≦ b で連続、a < x < b で可微分であるならば、
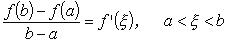
|
であるような ξ が存在する。
[ 演習 1.13 ] 平均値の定理を証明せよ。
区間 [ a , b ] において f ( x )、g ( x ) は連続で、( a , b ) において微分可能 とする。その時、( a , b ) 内のある点 ξ において、
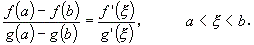
| (1.6) |
ここで、g ( a ) ≠ g ( b ) であり、f ( x )、g ( x ) は区間内で同時にゼロにはならないものとする。
[ 演習 1.14 ] コーシーの平均値の定理を証明せよ。
関数 w ( x ) はゼロ以上で、かつ [ a , b ] で積分可能、すなわち
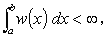
| (1.7) |
とし、f ( x ) は [ a , b ] で連続とする。この時、区間 [ a , b ] には、
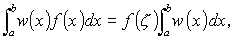
| (1.8) |
なる点 ζ が少なくとも1つ存在する。
[ 演習 1.15 ] 積分平均値の定理を証明せよ。
(註1)積分平均値の定理の幾何学的意味は、w ( x ) = 1 の時わかりやすい。なぜならば、
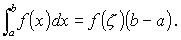
|
であるから。
関数 f ( x ) がある n ≧ 0 に対して閉区間 a ≦ x ≦ b(略して [ a , b ] )で n + 1 回微分可能であり、 x , x0 ⊆ [ a , b ] であるとする。この時、
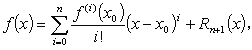
| (1.9) |
と書ける。ここで、f(0)( x0 ) = f ( x0 ) とする。また、 Rn+1( x ) は 剰余 (the remainder) と呼ばれる。 剰余には2種類がよく知られている:
|
[(註1)] (1.11) 式の剰余を(Atkinson, 1978, p.5) は積分表示している:
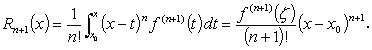 (1.12) (1.12)
[(註2)] (1.10) 式のコーシー型剰余は、つぎのシュレーミルヒの剰余
(the remainder term in the Schlomilch form) で q = n の場合の特別なケースである。ここで、
q は一般には、0 ≦ q ≦ n である。
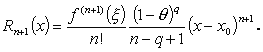
|
ここで、θ は、ξ = x0 + θ( x - x0 ) により定義される(小平、1976)。
[ 演習 1.16 ] テイラーの定理を証明せよ。
関数 f ( x ) がある n ≧ 0 に対して閉区間 a ≦ x ≦ b(略して [ a , b ])で n 回微分可能であり、 点 x = x0 で f(n+1)( x0 ) が存在し、x , x0 ⊆ [ a , b ] であるとする。この時、
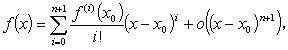
| (1.13) |
と書ける。
[ 演習 1.17 ] 定理13を証明せよ。
[例1] ex の x0 = 0 での テイラー展開
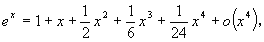
|
あるいは、
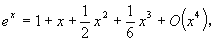
|
[例2] sin ( x ) の x0 = 0 におけるテーラー展開
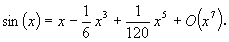
|
|
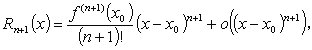 (1.14) (1.14)
と書くことにあたる。ここでは、さらに定理13の関数 f ( x ) は、n 回微分可能 であり、かつ点 x = x0 でのみ f(n+1)( x0 ) が存在すればよい点に注意。
その場合の Landau の記号による表現では剰余の位数は、展開の性質上、n-k/2(すなわち、 サンプル数 n の関数)となる。ここで、G ( x ) は単位(標準)正規分布の分布関数とする。
また、同じく分布関数 Fn( x ) が単位正規分布の分布関数 G ( x ) で近似できる場合、 Fn( x ) のパーセント点を G ( x ) のパーセント点で近似する問題を考えると、前者の下側 100 α パーセント点を Fn(-1)( α )、後者のそれを zα と書くと すると、 Fn(-1)( α ) は、
|
Atkinson, K. E. (1978). An introduction to numerical analysis, New York: Wiley.
Bowen, R. M., and Wang, C.-C. (1976). Introduction to vectors and tensors - Linear and multilinear algebra. New York: Prenum Press.
Bridges, D. S. (1998). Foundations of real and abstract analysis, New York: Springer.
Courant, R., and John, F. (1974). Introduction to Calculus and Analysis, Vol.2, New York: Wiley.
小平邦彦 (1976). 解析入門 II 岩波
高木貞治 (1971). 解析概論 改訂第三版 岩波
竹内啓編 (1987). 統計学辞典 東洋経済
宇野利雄 (1967). 微分積分学 I 共立出版
ここでは、第1章 微積分入門における演習問題の証明を行なう。それぞれの証明は、多くの場合、対応する 各証明の末尾に示した引用文献の証明を一部敷衍した。
(証明) まず、S は下方に有界であるとして、下限の存在を証明する。S の一つの下界を a とすれば、
a より小さな数もやはり S の下界である。ここで、S の下界であり得るすべての数を A(下組)とし、その他を
B(上組)とすれば、一つの(デデキントの)切断が定義できる。実際、B に属する数は、S の下界ではないので、
どんな下界より大である。したがって、A に属するどんな数よりも大である。この切断により決まる数を c とする。
この時、c は A に属して A の最大数であるか、さもなければ B に属して B の最小数である(公理1)。
ここで、c は B に属すると仮定してみる。この時、c は S の下界ではあり得ないので、c よりも小さくかつ S
に属する数 x が存在する。すなわち、x < c である。つぎに、x と c の中間のある一つの数を b とする。すなわ
ち、x < b < c とする。この時、b は Sに属する数 x より大なので、S の下界ではない。すなわち、b は B に属す
る。しかし、b は c より小なので、矛盾する。したがって、c は B の最小数ではない。故に、c は Aの最大数、す
なわち S の最大下界すなわち S の下限である。
S が上方に有界なとき上限が存在することも、上と同様にして証明できる。□
(高木, 1973, p.5).
(証明) ある正数 ε を取れば、仮定により n > p のとき、| c - an|< ε、 すなわち
c - ε < an < c + ε なる自然数 p が存在する。そこで、| ai|, i = 1 , ... , p、
| c - ε |、及び | c + ε | のいずれよりも大きい数 M を取れば、任意の n に対して | an
|< M が成り立つ。
つぎに、an → c かつ | an| < M とする。もし、ここで| c | > M だと仮定すると、
| c | > M ' > M なる M ' が存在する。このとき、| c - an | > M ' - M > 0 となる。これは、
an → c と矛盾する。□
(高木, 1973, p.6).
(証明) 簡単のため2次元の場合を証明する。この集合 S は有界なので、すべての辺がx 軸か y 軸に
平行な一つの正方形に含まれると考えてよい。Q には S の無数の点が含まれるので、Q を4つの正方形に等分
すれば、これらのうち少なくとも一つはその内部または周上に S の無数の点を含む。その一つを Q とする。
そのような正方形が二組以上あるときは、例えば象限順の最初のものを取るとする。
同様に、Q1 は S に属する無数の点を含むので、Q1 を4つの正方形に等分すれば、
それらのうち少なくとも一つ(それを Q2 とすれば)は、必ず S の点を無数に含まねばならない。
このようにしていけば、Q1, Q2 , ... , Qn , ... なる正方形の列が生じ、
n → ∞ のとき、Qn の辺は限りなく小さくなる。
ここで、常に Qn の4つの頂点の中で左下のもの(各座標が最小になるもの)を( an
, bn ) とすれば、Q ⊃ Q1 ⊃ Q2 ⊃ ... Qn ⊃ ... なので、
a ≦ a1 ≦ a2 ... ≦ an ≦ ... 及び b ≦ b1 ≦ b2
... ≦ bn ≦ ... が成り立つ。これら2つの数列は明らかに有界なので、定理3から、limn→
∞an = α , limn→∞bn = β が言える。そこで、点 P = ( α , β )
は集積点である。
なぜならば、今 ( α , β ) を中心とするどれだけ小さな円を取ってみても、十分大きなある番号以上は、
Qn はすべてその円に含まれる。しかし、Qn は S の点を無数に含むので、どれだけ
( α , β ) に近いところにも S の点が無数に存在する。□
(高木, 1973, pp.14-15).
(証明) まず、有界な閉区域 K において連続な関数 f ( P ) は有界であることを証明する。最初に、
上界について証明する。もし、f ( P ) が上界を持たないとすれば、f ( P0 ) > 0 なる点 P0
がある。同様に、f ( P1 ) > 2f ( P0 ) なる点 P1、f ( P2 )
> 2f ( P1 ) なる点 P2 等がある。
P1 , P2 , ... は無数の相異なる点で、K が有界なる閉領域なので、K において集積点
が存在する(定理4)。その一つを A とする。
ここで、P1 , P2 , ... の部分列で A に収束するものを Pα1
, Pα2 , ... とする。このとき、limn→∞ f ( Pαn
) = f ( A )。しかし、このことは、f ( Pαn > 2αnf ( P
0 ) であり、αn は限りなく大きくなるので、これは不合理である。したがって、f ( P ) は上
界を持つ。
下界についても同様である。 □
(高木, 1973, p.27).
(証明) まず、S = [ a , b ] を、a ≦ x ≦ b なる点の集合とする。もし、 f ( x ) が S 上のどの点
でも連続だとすれば、任意の正数 ε を与えたとき、S 上のどの点 ξ1 に対しても、S 上の任意の点
ξ 2 に対して | f ( ξ 2 ) - f ( ξ 1 ) | < ε / 2 なる半径 δ = δ
( ξ 1 ) なる ξ 1 の δ- 近傍 ( δ- neighborhood ) が存在する(なぜならば、関数
が連続ならば、定義4よりどの点でも極限が存在し、f ( x ) に等しい。そこで、定義2より)。
つぎに、S 上のそれぞれの点 ξ 1 に対して、半径 ( 1 / 2 ) δ ( ξ 1 ) なる近傍
Ω P を考えよう。Ω P は、明らかに S を覆う。われわれは、それらの中から、やはり
S を覆う中心 ξ 1 , ξ 2 , ... , ξ n を持つ有限個の点を選ぶことができ
る。つぎに、( 1 / 2 ) δ ( ξ 1 ) , ... , ( 1 / 2 ) δ ( ξ n ) の中の最小な値を
ζ と書くことにしよう。このとき、もし ξ 1 と ξ 2 が S 上で距離が ζ より小さい
ところの2点であるならば、点 ξ 1 は点 ξ k , k = 1 , ... , n の中の1つからの距
離が ( 1 / 2 ) δ ( ξ k ) より小さい。ζ ≦ ( 1 / 2 ) δ ( ξ k ) なので、点 ξ
1 と ξ 2 は共に ξ k の δ ( ξ k ) - 近傍内に位置する。そ
こで、
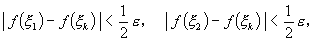
| (A.1) |
となり、そこで、
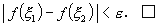
|
(Courant & John, 1974, pp.112-113).
(証明) まず、α < μ < β として、F ( x ) = f ( x ) - μ を定義する。この時、F ( a ) = α
- μ < 0 かつ F ( b ) = β - μ > 0。また、F ( x ) は [ a , b ] で連続で、F ( a ) < 0 なので a のあ
る近傍では F ( x ) < 0。そこで、[ a , η ] で常に F ( x ) < 0なる η が存在する。しかし、F ( b ) >
0 なので η < b。つまり、そのような η には上限がある。それを ξ とすれば、F ( ξ ) = 0 でなければな
らない。
ここで、もし F ( ξ ) < 0 ならば、区間 [ a , η ] は ξ を超えて延長される。それは ξ の意味(つま
り、(1) 式の成立)に反する。一方、もし F ( ξ ) > 0 ならば、十分小さな ε に対して F ( ξ - ε ) > 0
で、[ a , η ] の右端 η は ξ - ε を超えない。それも ξ の意味に反する。そこで、F ( ξ ) = 0 、すな
わち f ( ξ ) = μ。また、(前述の議論で、区間の右端には上限があるとの結果から)a < ξ ≦ b であったが、
f ( b ) = β ≠ μ なので、ξ < b。□
(高木, 1973, p.27).
|
(宇野、1967, p.18)。
|
(宇野、1967, p.19)。
|
(宇野、1967, pp.22-23)。
(証明)
|
(宇野、1967, p.26, pp.55-56)。
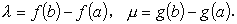
| (A.12) |
この時、
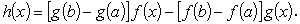
| (A.13) |
この時、ロルの定理から h '( ξ ) = 0 なる ξ が 4a < ξ < b に存在する。
そこで、
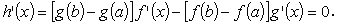
| (A.14) |
そこで、
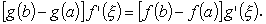
| (A.15) |
ここで、g ' ( ξ ) はゼロでない。なぜならば、もし g '( x ) = 0 ならば定理の仮定1、
すなわち g ( a ) ≠ g ( b ) より、f '( ξ ) = 0 となるが、このことは仮定2に反する。
そこで、(A.15) 式の両辺を [ g ( b ) - g ( a ) ] g '( ξ ) で割れば、定理の式を得る。 □
(高木、1973, pp.48-49)。
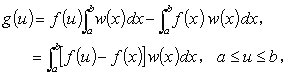
| (A.16) |
を定義する。
g ( u ) は、f ( u ) の定数倍にもう1つの定数を加えたものに等しいので、[ a , b ]
で連続である。中間値の定理(定理2'の方)における点 p を用いると、
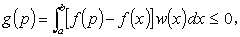
| (A.17) |
が成り立つ。なぜならば、f ( x ) の区間 [ a , b ] での下限 (infimum) を与える点 p に対して、
中間値の定理より [ a , b ] で f ( p ) - f ( x ) ≦ 0 が成り立つので。その結果、g ( p ) は
正にはならない。
同様にして、f ( x ) の [ a , b ] での上限 (supremum) を与える点 q に対して、
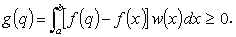
| (A.18) |
(A.17)、(A.18) 式より、g ( u ) は p と q の間の点 ζ でゼロでなければならない。 □
(Atkinson, 1978, pp.4-5)。
|
|
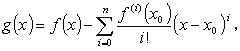
|
とする。
今回は、定理12と異なり f ( x ) は n 階まで微分可能なので、コーシーの平均値の定理により、
g ( x ) と h ( x ) = ( x - x 0 )n+1 に対して、
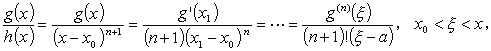
| (A.35) |
そこで、g(n)( x 0 ) = 0 に注意すれば、x → x 0 したがって、 ξ → x 0 のとき、
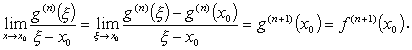
| (A.36) |
すなわち、
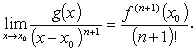
| (A.37) |
つまり、
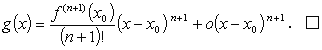
| (A.38) |