このページは、令和2年5月7日に一部更新しました。
上のプログラムの中の3つ目と4つ目の freq プロシジャは、2つ及び3つ以上 のカテゴリー変数間の分割表の検定のためのものである。前者の結果をまず示す とつぎのようになる;
TABLE OF CAT2 BY CAT6
CAT2(SEX) CAT6(EVALUATION OF ZEN INSTRUCTIONS)
Frequency |
Expected |
Cell Chi-Square|
Percent |
Row Pct |
Col Pct |too seve|appropri|more sev|
|re |ate |erely | Total
---------------+--------+--------+--------+
male | 27 | 275 | 75 | 377
| 22.004 | 292.65 | 62.344 |
| 1.1344 | 1.0647 | 2.569 |
| 5.25 | 53.50 | 14.59 | 73.35
| 7.16 | 72.94 | 19.89 |
| 90.00 | 68.92 | 88.24 |
---------------+--------+--------+--------+
female | 3 | 124 | 10 | 137
| 7.9961 | 106.35 | 22.656 |
| 3.1217 | 2.9298 | 7.0696 |
| 0.58 | 24.12 | 1.95 | 26.65
| 2.19 | 90.51 | 7.30 |
| 10.00 | 31.08 | 11.76 |
---------------+--------+--------+--------+
Total 30 399 85 514
5.84 77.63 16.54 100.00
STATISTICS FOR TABLE OF CAT2 BY CAT6
Statistic DF Value Prob
------------------------------------------------------
Chi-Square 2 17.889 0.000
Likelihood Ratio Chi-Square 2 20.400 0.000
Mantel-Haenszel Chi-Square 1 2.745 0.098
Phi Coefficient 0.187
Contingency Coefficient 0.183
Cramer's V 0.187
Sample Size = 514
|
上の出力結果のカイ二乗検定の統計量の値をみると、17.889 で、危険率に 対応する Prob の値は、0.01 より小さい。したがって、この結果は、分割表の 行カテゴリーである性別と列カテゴリーである座禅指導の評価の間には、1%水準 以上の高い水準で統計的に有意な関連があることがわかる。
一般的には、分割表のカイ二乗検定は、つぎの統計量による。ここで、分割表 の行、列属性をそれぞれ A 、B 、行数、列数をそれぞれ r 、s とし、総 度数を N とする。この時、帰無仮説 H 0 :2つの属性 A 、B は互いに 独立(関連無し)、のもとでは、各セルの期待度数が5より大の時:
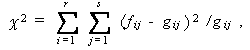
|
(1.1) |
は、近似的に自由度 ν =(r-1)(s-1) なる χ2 - 分布に従う。ここで、
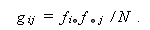
|
(1.2) |
(1.2) 式の gij は、2つの属性 A 、B が互いに独立(関連無し)の もとで (i ,j ) セルに期待される度数であり、 期待度数 (expected frequency) と呼ばれている。
また、(1.1) 式から明らかなように、この式の左辺の χ2 は、各セルに ついての次式で与えられる量 hij の和、として定義されているので、hij は、セルカイ2乗と呼ばれ、全体的なカイ2乗に対する各セルの寄与の程度を表している。したがって、 帰無仮説が棄却された場合には、上の期待度数とこの量 hij を同時に出力 できていれば、2つの属性 A 、B のどこにとりわけ大きな独立性からのずれが どの方向にあるのかを検討できることになる。
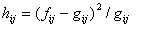
|
(1.3) |
上の SAS プログラムを見ると、すべての freq プロシジャで tables 文の オプション(tables 文の後ろの方の / 記号の後)の中に expected と cellchi2 が入っていることがわかる。この指定により、それぞれ期待値とhij が、 出力結果に示される。これらは、分割表の右上に英字でそれぞれ expected 及び Cell Chi-Square として表示されていることが、上の出力例からわかる。
上の出力例で具体的に見てみると、後者の値の相対的に大きいセルは、(2,3) セル、(2,1) セル、(2,2) セル、及び (1,3) セルであることがわかる。 これらの値、及びそれに対応するセルの期待度数の実度数からの乖離の方向から、 例えば女子は相対的には座禅指導をもっと厳しくして欲しいと思 ったものが少 なく((2,3) セル)、男子はその逆((1,3) セル)であると言える。
上の SAS プログラムのうちの最後の freq プロシジャでは、cat4 変数と cat1 から cat3 までの変数のそれぞれとの分割表の作成とそれらの検定を指示するもの である。この場合、オプションで nocol、及び norow を指定しているので、各 セルの指標のうち列及び行パーセントは出力が抑止される。
セルカイ2乗を用いた上記の分析は、あくまでも記述レベルにとどまるが、これについて の検定も可能である。ここで、つぎの量を定義しよう。この量は調整後の残差 (adjusted residuals) と呼ばれる:
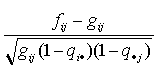
|
(1.3a) |
ここで、 (1.3a) 式で、qi・=fi・/N 及び q・j=f・j/N である。
この時、うえの量は、2つの属性間に関連がないという帰無仮説のもとでは、サンプル数が 大の時近似的に標準正規分布をすることがわかっているので、これを利用できる(Agresti, 1996, p.31) 。
最後に、分割表の検定では一般にサンプル数が小さいときにはカイ2乗分布が 歪むことが知られている (Yates, 1934)。Yates によれば、分割表のカイ2乗検定 でカイ2乗が歪む原因は、もともと統計学的分布としてのカイ2乗分布その ものは連続分布であるのに対して、分割表の検定のための(ピアソンの)統計量は、 (1.1) 式から明らかなように、非連続(離散)分布であることによる。また、歪みの 方向は、一般にリベラルな方向であることも知られている。その原因の1つは、このよ うな場合の正確な検定として知られているあとで述べる Fisher の直接確率法で は分割表の周辺度数は固定との条件が仮定されているが、一般の分割表では必ず しも周辺度数は固定されておらず、そのような場合、検定は相対的にリベラルとなる ことがわかっているからである。
ここで、サンプル数の小ささの目安は、各セルの(期待)度数のいずれかが5以下 かどうか、である。本邦のテキストの中には、「各セルの度数が5以下のものがあ る」という表現を使っているものも2、3見られるのに対して、欧米のテキストでは 期待度数が5以下のもの (例えば、Guilford, 1973; McNemar, 1969) という表現を しているものが多いようである。また、竹内啓編の統計学辞典では、「標本数が 少ない(たとえばセルの期待度数が5未満の時」という表現をしているものもある。 (1.1) 式の分布は、2つの属性間に関連がない、という帰無仮説のもとでの分布で あるから、そのような場合、平均的には実度数は期待度数に近い、といえるので、 「実度数が5以下」という表現も間違いとまでは言えないであろうが、実度数はあく までも実現値でしかないので、目安としては期待度数の方がより適切であろう。 いずれにせよ、セル内に期待度数5以下の度数が存在する場合には、つぎのように イエーツの修正 (Yates' correction in chi square) を行うとよい(SAS 方式):
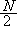 の時、(7.4) 式の分子の ad - bc を
ad - bc -
の時、(7.4) 式の分子の ad - bc を
ad - bc -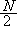 とする。
とする。
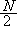 以下の時は、
(7.4) 式のカイ2乗値をゼロとする。
以下の時は、
(7.4) 式のカイ2乗値をゼロとする。
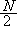 の時、(7.4) 式の分子の ad - bc を
ad - bc +
の時、(7.4) 式の分子の ad - bc を
ad - bc + 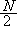 とする。
とする。
SAS では、この方式によるカイ2乗値と対応する p-値が以下の出力結果の中の Continuity Adj. Chi-Square (日本語バージョンでは、連続性補正カイ2乗値)と して、表示される。
一方、このような場合に対処する根本的な方法は、ノンパラメトリックな方法である Fisher の直接確率法を用いることである。SAS では、2×2 分割表の場合に は何も指定しなくても、カイ2乗と同時に Fisher の直接確率も計算するが、一 般の r × s 分割表の場合にはオプションに exact を指定しないとこ れを計算してはくれない。
ここでは、上の永平寺データのカテゴリー変数のうち、cat5 の3カテゴリーを 2カテゴリーに合併して cat2 すなわち性別との2×2 分割表とした時の 結果を示してみよう。
fisher's exact probability
TABLE OF CAT2 BY DOG
CAT2(SEX) DOG
Frequency |
Expected |
Cell Chi-Square|
Percent |
Row Pct |
Col Pct | 1| 2| Total
---------------+--------+--------+
1 | 77 | 300 | 377
| 65.278 | 311.72 |
| 2.1048 | 0.4408 |
| 14.98 | 58.37 | 73.35
| 20.42 | 79.58 |
| 86.52 | 70.59 |
---------------+--------+--------+
2 | 12 | 125 | 137
| 23.722 | 113.28 |
| 5.7922 | 1.2129 |
| 2.33 | 24.32 | 26.65
| 8.76 | 91.24 |
| 13.48 | 29.41 |
---------------+--------+--------+
Total 89 425 514
17.32 82.68 100.00
STATISTICS FOR TABLE OF CAT2 BY DOG
Statistic DF Value Prob
------------------------------------------------------
Chi-Square 1 9.551 0.002
Likelihood Ratio Chi-Square 1 10.697 0.001
Continuity Adj. Chi-Square 1 8.753 0.003
Mantel-Haenszel Chi-Square 1 9.532 0.002
Fisher's Exact Test (Left) 1.000
(Right) 9.56E-04
(2-Tail) 1.50E-03
Phi Coefficient 0.136
Contingency Coefficient 0.135
Cramer's V 0.136
Sample Size = 514
|
出力結果から明らかなように、この場合にはどのセルも実度数が5以下にはなって いないので、わざわざ Fisher の直接確率を計算する必要はないことになる。しかし、 もし実度数が5以下になるようなセルがあれば、上の統計量のうち Fisher の直接 確率の部分、とりわけ通常は (2-Tail) に対応する p -値、すなわち Prob の値 を見る必要がある。