このページは、令和2年5月7日に一部更新しました。
最後に、INV 5尺度相互の関連性の有無についてみてみよう。このような定量的 変数の場合には、前節で計算したような関連性の指標ではなく、 ピアソンの偏 差積率相関係数(Pearson's product-moment correlation coefficient)、略して 相関係数を計算する必要がある。相関係数は、一般につぎの式で 計算される:
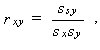
|
(1.4) |
したがって、この例のように5尺度あると、相関係数は合計10個存在する。うえの プログラムの3番目にあるように、SAS では corr プロシジャを用いると、これら すべての間の相関係数を計算するばかりでなく、それぞれが統計的に有意かどうかの 検定まで出力してくれる。これを示したのが、つぎの表である。
Pearson Correlation Coefficients / Prob > |R| under Ho: Rho=0 / N = 50
INV1 INV2 INV3 INV4 INV5
INV1 1.00000 0.31087 0.21898 0.37505 0.16923
INV循環性 0.0 0.0280 0.1265 0.0073 0.2400
INV2 0.31087 1.00000 0.25720 0.49903 0.40196
INV粘着性 0.0280 0.0 0.0714 0.0002 0.0038
INV3 0.21898 0.25720 1.00000 0.47174 0.54859
INV分裂性 0.1265 0.0714 0.0 0.0005 0.0001
INV4 0.37505 0.49903 0.47174 1.00000 0.40479
INVヒステリー 0.0073 0.0002 0.0005 0.0 0.0035
INV5 0.16923 0.40196 0.54859 0.40479 1.00000
INV神経質 0.2400 0.0038 0.0001 0.0035 0.0
|
相関係数の推定・検定は、一般的につぎのようにして行う。
サンプル数が小さい時には、母集団の相関係数 ρ がゼロなる帰無仮 説 H0: ρ =0 のもとで、標本相関係数から作るつぎの量 t
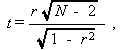
|
(1.5) |
が、自由度 ν =N -2 の t -分布に従うことを利用する。
(註1)この式は、Fisher (1915) による相関係数の分布の一般形の(母相関 がゼロの)特殊ケースである(例えば、Kendall and Stuart, 1973, Vol.1, p.415)。 したがって、上記統計量 t はサンプル数にかかわらず正確 (exact) である。
この場合は、r が大で母相関係数がゼロならば、r は近似的に平均ゼロ なる正規分布に従うことを利用する。この時、r の標準誤差は 1/sqrt(N) である (McNemar, 1969)。
(註2)r の分散(標準誤差の二乗)の一般形は知られている(例えば、 Kendall and Stuart, 1973, Vol.1, p.251) が、McNemar によるそれは、 r の分散の一般形で、分布が2変量正規分布かつ母相関係数がゼロの場合 にあたる。
母相関係数が任意の場合、その信頼限界の推定や検定には、標本相関係 数を z 変換(Fisher, 1921)
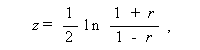
|
(1.6) |
した場合、任意の母相関係数に対して近似的に正規分布に近づくことを利用する。
また、小さな母相関係数に対しては、
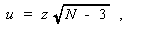
|
(1.7) |
とした時の u が、近似的に正規分布に従うことを利用する。
(註3)任意の母相関係数の場合の相関係数 r の(標本)分布の正確な形(一般 に は正規分布ではない)は、Fisher (1915) が示しており複雑な分布関数の形を している。ここで、サンプル数が大きくなると、分布はゆっくりと正規分布に 近づく(同上、Kendall & Stuart, 1973, Vol.2, p.415-416)。
上の相関行列の出力結果のうち、各セルの上段が2つの変数間の相関係数であり、 下段が検定結果の p 値、すなわち母相関がゼロのもとで標本相関係数の値の 絶対値以上の値を取る確率が示されている。この値が 0.05 以下ならば、相関係数 は統計的に有意と言える。
この点を考慮して上の相関行列の出力結果を見ると、5つの尺度間には複雑な相 関関係があることがわかる。もっとも、相関係数が統計的に有意と言っても、そのこと 自身は両変数間に直線的な関係があると言っているだけであり、両変数間の標本 としての具体的な関係を明らかにしているわけではない。
これを見るには、上のプログラムの最後にある plot プロシジャを用いてやる とよい。この例は、数ある有意な相関のある対の中から、inv2 と inv1 及び inv5 と inv3 との間の具体的な関係を散布図として描かせるためのものである。 出力結果は、つぎのようになる。図中、A はその位置に落ちる度数が1である ことを、B は、その位置に落ちる度数が2であることを表している。
scatter diagram
プロット : INV2*INV1. 凡例 : A = 1 OBS, B = 2 OBS, ...
|
|
15 + A A
14 + A A A
I 13 + A A
N 12 + A A A A
V 11 + A A
粘 10 +
着 9 + A A A A
性 8 + A A A A
7 + A A A A A A
6 + A A B A
5 + A A
4 + A A A A
3 + A B A
2 + A A A A A A
1 + A A
|
---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+--
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
INV循環性
scatter diagram
プロット : INV5*INV3. 凡例 : A = 1 OBS, B = 2 OBS, ...
|
16 + A A
15 + A A
14 + A
13 + B A
I 12 + A A A A
N 11 + A A
V 10 + A
神 9 + A A A A A
経 8 + A A A
質 7 + A A A B A
6 + A A A B A A
5 + A B
4 + B A B
3 + A
2 + A A A A
1 +
0 + A
|
---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+--
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
INV分裂性
|