このページは、平成11年8月3日に一部更新しました。
このページは、令和2年5月7日に一部更新しました。
前節では、定量変数間の相関係数の定義や、SAS による相関係数の計算と出力 結果について述べた。相関係数は、多くの多変量解析の基本となる指標であるが、 データの中に異常に大きな値や小さな値を持つサンプルを含む場合には、この値が 大きく変動し、場合によっては相関係数の検定結果にも大きく影響するので、注意が 必要である。ここでは、簡単な具体例を示し、はずれ値の重要性に言及する。
つぎの散布図は、浮田・横井ら (1996) による被験者48名のクレペリン精神 作業検査における休憩後の動揺率を横軸に、同休憩後の平均誤答率を縦軸にした 2変数の散布図である。この図右上の被験者の両変数の値は共に、他の被験者の それからはかなりかけ離れた値を示している。
プロット : ERRORA1*EXCITEA1. 凡例 : A = 1 OBS, B = 2 OBS, ...
| 休憩後
| 平均
5 + 誤答率
|
|
| A
|
4 +
|
|
|
|
3 +
|
|
|
|
2 + A
| A A
|
|
| A A
1 + A A
| A B A
| A AA A A A A
| AA ABBB A AA
| AAAAB A BA A A
0 + BA A A
|
--+-----------+-----------+-----------+-----------+-----------+-----------+-
0.0 0.2 0.4 0.6 0.8 1.0 1.2
休憩後動揺率
|
ちなみに、両変数間の相関係数は 0.692 であり、1パーセント水準以上の高い 水準で統計的に有意である。しかし、もしうえのはずれ値を1つ除くと、相関係数は 劇的に 0.253 と小さくなり、もはや5パーセント水準でも有意ではなくなる。 はずれ値をはずした場合の両変数間の散布図は、つぎのようになる:
プロット : ERRORA1*EXCITEA1. 凡例 : A = 1 OBS, B = 2 OBS, ...
2.0 + 休憩後
| 平均 A
| 誤答率
| A
| A
|
|
1.5 +
|
|
|
|
| A A
| A
1.0 + A
|
| A
| A B
|
| A A
| A A
0.5 + B A A
| A AAA
| A A AA A A A
| A A
| AA A A A A A
| AA A
| AA
0.0 + A A A
-+-----------+-----------+-----------+-----------+-----------+-----------+
0.1 0.2 0.3 0.4 0.5 0.6 0.7
休憩後動揺率
|
もう1つの例は、千野のホームページの講義ノート「反復測定デザイン分散分析/基礎と応用」
の中の第1章
1.5.5 節の鏡映描写
実験データである。ここで、その節のプログラム中のデータは A 大学心理学科の25名の学生によ
る鏡映描写実験における星形図形一周に要した所要時間を、事前テスト、7回の練習試行、事後
テストの順に並べたものである。測定単位は秒である。
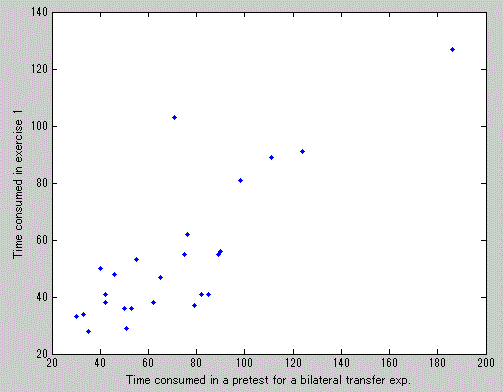
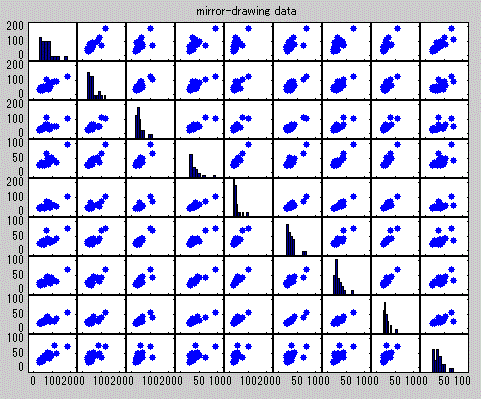
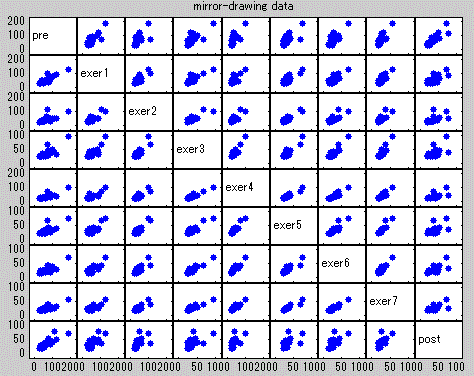
つぎの表は、まず最初に、25名の原データに対する上記9条件から成る変数間の散布図を非対角部分に、
また対角部分には各変数の度数分布を MATLAB によって描いたものである。また、つぎの表には、
対角部分に度数分布の代わりに変数名を記したものである。これらを見ると、このデータにも1、
2の外れ値が存在することがわかる。
つぎの図は、うえの表の中の事前テストの成績 (pre) を横軸に、第1試行の成績 (exer1) を縦軸 に取った時の散布図を拡大したものである。