第２章 重回帰分析

このページは、令和２年５月７日に一部更新しました。

　われわれが予測ないしは説明したい複数の変数、すなわち 予測変数（ predictor variables）でもって、ある変数（これは従属変数 dependent variable、 あるいは 基準変数 criterion variable と呼ばれる）の値の変動を予測 ないしは説明したいとする。この時、N 人の被験体のそれぞれに対し、両変数 の値を観測した結果は、Table 2.1 のように書ける。

表2.1: 重回帰分析データの一般形

基準変数の値	m 個の予測変数の値
y1	x11 , x12 , ... , x1m
y2	x21 , x22 , ... , x2m
	...
yN	xN1 , xN2 , ... , xNm

　 重回帰分析（multiple regression）では、このようなデータから出発して、 予測変数全体で、基準変数をどれ程説明できるか、及びもし予測ないし説明 できるとしたら、どの予測変数がどれほど基準変数を説明できるかなどを 検討する。

　重回帰分析における変数は、予測変数、基準変数共に、通常は評定尺度や検査得点 のような間隔尺度レベルで測定されていなければならない。

　分散分析における測定値を基準変数、これに影響するとみなし実験配置する要因 （処理）を予測変数とみなせば、分散分析と重回帰分析は、共に基準変数に対する 予測変数の効果の有無を検討する方法と言える。 　一方、両者の相違点をあげれば、分散分析では予測変数をあらかじめできる限り 絞り込み、少数の変数（要因）についてその水準をカテゴリー化し、要因の水準の 組み合わせに対して被験者を無作為に割り付けるのを原則とするのに対して、重回 帰分析では予測変数はそれほど絞り込まず、通常はそれらの変数をカテゴリー化せず、 すべての被験者にすべての変数に対する測定を行うという点である。

２.１節　重回帰分析の例とモデル

　Table2.2.は、この種の具体例を示す。データはA大学心理学科のある年度の C ゼミ の１３名の受講生の卒業論文の成績及び１年次から３年次までの各学年での学業成績 （平均）である。このデータの分析の目的が、

1. 卒業論文の成績は、３年間の成績により説明ないし予測可能か？
2. もし予測可能であれば、何年次の成績が卒業論文の成績を最も良く 説明するか？

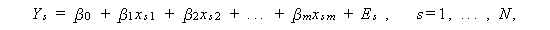
(2.1)

と書かれる。ここで、 β₀ ,β₁ , ... ,β_m は 回帰係数 (regression coefficients) と呼ばれる。 m ≧ 2 の時、これらは 偏回帰係数 (partial regression coefficients) と呼ばれる。また、E_s は、誤差変動で、

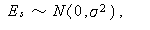
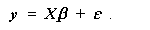
(2.2)

y = (Y1 ,Y2 , ... , YN ) t,
	(2.3)
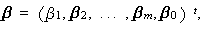
	(2.4)
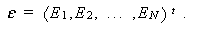
	(2.5)