２.２節 偏回帰係数の推定
このページは、令和２年５月７日に一部更新しました。
ここで、Ys の予測値
|
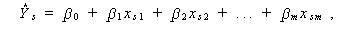
(2.6) |
と実測値 Ys =ys の差をサンプル全体に亘り最小にするような β0 , β1 , ... ,βm のうち、β0 に関しては、そのような β0 は、
|
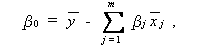
(2.7) |
であることが容易に証明できるので、X 、β から β0 に 関する項を落とし、確率変数 Ys の変わりに実現値としての ys を用いて、
|
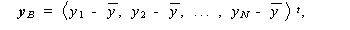
(2.8) |
|
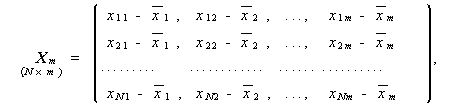
(2.9) |
|
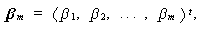
(2.10) |
と置くと、モデルによる yB の推定値
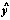B は、
|
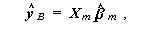
(2.11) |
とも書ける。
ここで、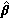
m は、もとのモデルの誤差をサンプル全体に亘り最小にする
ような偏回帰係数ベクトルの推定値ベクトルであり、
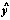B は、
それによる予測値ベクトルの推定値ベクトルである。
βm の最小二乗
推定量は、
|
である。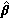m は、つぎのようにも書ける。
|
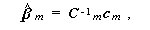
(2.13) |
あるいは、
|
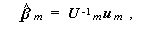
(2.14) |
ここで、
|
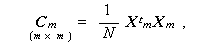
(2.15) |
|
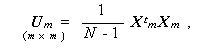
(2.16) |
|
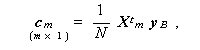
(2.17) |
|
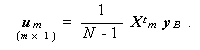
(2.18) |
ここで行列 Cm は、標本共分散行列、Um は標本不偏共分散行列、 ベクトル cm は、基準変数と予測変数との間の標本共分散を、同じくベク トル um は標本不偏共分散を縦に並べたものである。
さらに、
| Dm = diag {sj } (あるいは diag {uj }) . | (2.19) |
|
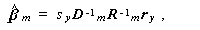
(2.20) |
とも書ける。ここで、Rm は、標本相関行列（sample correlation matrix）で、
|
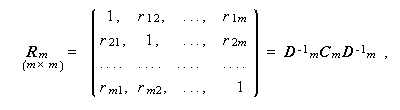
(2.21) |
|
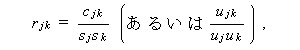
(2.22) |
|
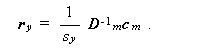
(2.23) |
また、この時、
|
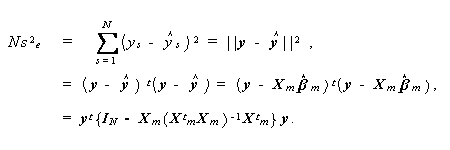
(2.24) |
ここで、
| Ns2y = ||yB||2 = ytByB , | (2.25) |
|
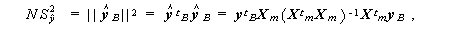
(2.26) |
であることが容易に証明できるので、上の関係から、
|
