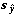 2 の比は、(2.27) 式から
2 の比は、(2.27) 式から
重回帰分析における基準変数の全変動 s2y に占める推定値変
動 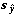 2 の比は、(2.27) 式から
2 の比は、(2.27) 式から
|
と書け、 重相関係数の二乗(squared multiple correlation coefficient)と呼 ばれ、SMCと略記する。ここで、

|
(2.29) |
すなわち、
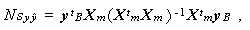
|
(2.30) |
が N 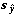 2 に等しいことに注意すると、
2 に等しいことに注意すると、
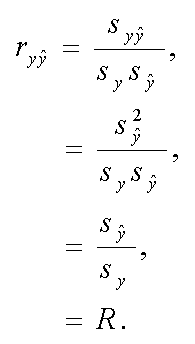
|
(2.31) |
すなわち、上の重相関係数は、基準変数の実測値と予測値の間の 相関係数にあたることがわかる。
|
であることは明らかである。
つぎに、標本重相関係数 R2 から、母重相関係数 R20 の検定を行う 方法について述べる。
その前に、yB を y で表わす行列表現に注意しておこう。付録 5の(7)、(8)式より、
| yB = Gy . | (2.33) |
ここで、
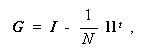
|
(2.34) |
すなわち、行列 G は、
| Gt = G , | (2.35) |
| G2 = G , | (2.36) |
なる性質を持ち、べき等行列の1つである。
この性質を利用すると、(2.25)式のNs2y は、
| Ns2y | = ytByB = ytGtGy = ytGtGGY , | |
| = ytBGyB . | (2.37) |
とも書ける。同じく付録5の定理等を用いると、rankG = N -1 に注意して、
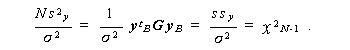
|
(2.38) |
すなわち、ssy/σ2 は、自由度 N -1 のχ2 -分 布に従うことがわかる。
一方、s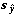 /σ2
については、
(2.26)式の右辺の二次形式の行列 Xm (Xtm
Xm ) -1Xtm
がやはりべき等行列であること(付録5)および、
/σ2
については、
(2.26)式の右辺の二次形式の行列 Xm (Xtm
Xm ) -1Xtm
がやはりべき等行列であること(付録5)および、
| rank {Xm (X tmXm ) -1X tm } = m , | (2.39) |
であることに注意すると、
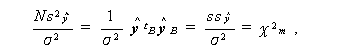
|
(2.40) |
すなわち、s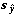 /σ2 は、自由度 m のχ2 -分布に従う
ことがわかる。
/σ2 は、自由度 m のχ2 -分布に従う
ことがわかる。
さらに、(2.27)式より、
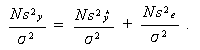
|
(2.41) |
これにより
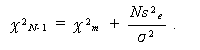
|
(2.42) |
カイ二乗の加法性の性質(問1.1.1の解答、定理3)から、
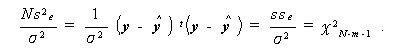
|
(2.43) |
すなわち、sse/σ2 は、自由度 N -m -1 のχ2 -分布に従うことが わかる。 ここで、(2.24)式より、sse/σ2 の二次形式の行列 IN - Xm (XtmXm ) -1Xtm も、やはりべき等行列であることが容易に証明できる。さらにうえの結果から、
| rank { IN - Xm (XtmXm ) -1Xtm } = N -m -1 , | (2.44) |
であることもわかる。
これらより、帰無仮説
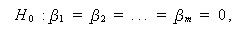
|
(2.45) |
のもとでは、
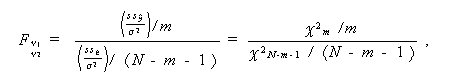
|
(2.46) |
は、自由度 ν1 =m , ν2 = N -m -1 の F -分布に従うことがわかる(問1.1.1の
解答の定理1参照)。
(2.46)式の F 比は、s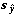 、sse の定義から結局、
、sse の定義から結局、
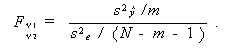
|
(2.47) |
ここで、(2.27)、(2.28)式に注意すると、
|
このことは、重相関係数に関する帰無仮説 H0 (R0 )
| H0 (R0 ) : R0 = 0 , | (2.50) |
を危険率 α で棄却することに等しい。