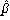２.４節　 偏回帰係数とその検定

　 (2.45)あるいは(2.50)式の帰無仮説が棄却されたならば、つぎに、どの予測 変数が基準変数の予測に効いているのかを各偏回帰係数の検定により検討する。 このためには、各偏回帰係数の推定値 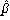_j , j =1,2, ... ,m の 期待値と分散を知る必要がある。

　 ここで、各 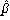_j は、(2.12)式で表わされ、行列 X_m の要素は (2.1)式より確率変数ではなく定数であること、(2.12)式の右辺の観測値ベクト ル y_B の要素は確率変数 Y_s ,s =1,2, ... ,N の実現値であること、偏回 帰係数の推定値ベクトル 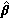_m は確率変数の実現値ベクトル y_B の 一次関数になっていること、の３点を考慮すると、 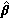_m は、母偏 回帰係数ベクトル β_m の１つの実現値であり分布を持つことに注意したい。

　 モデルの誤差変動 E_s ,s =1,2, ... ,N は互いに独立で、平均ゼロ、分散 σ² の正規分布に従うという仮定から、まず、

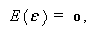
	(2.51)
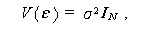
	(2.52)

ここで、

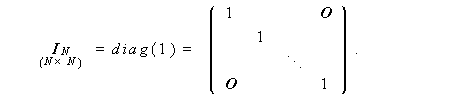
　 つぎに、(2.2)式を y_B を用いて書くと、

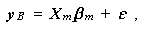
(2.53)

となることを用いて、(2.12)式を書き換えると、

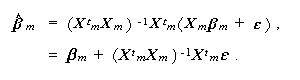
(2.54)

　 そこで、(2.51)式に注意すると、

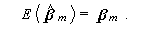
(2.55)

　 さらに、(2.54)式、(2.52)式に注意すると、

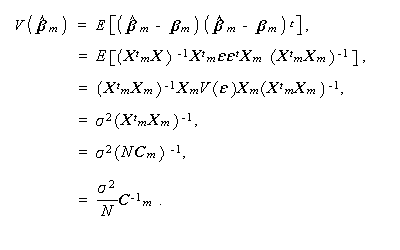
(2.56)

　 そこで、推定量 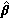_m の標準誤差は、

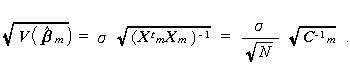
(2.57)

　 もし、ここで σ が未知であるとすれば、σ² の不偏推定量 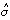_u

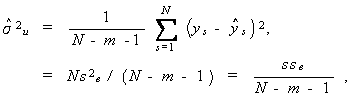
(2.58)

の平方根をこれにあてる。σ² の推定については後述する。 　 いずれにせよ、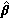_m の期待値と分散はわかった。それで は 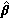_m の分布形はどうなるであろうか。これについては、(2.12) 式から、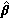_m は、y_B の要素が正規分布に従い、 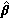_m が y_B の一次結合になっているので、 やはり正規分布に従う。
　 ここで、標準化された正規変量 Z および自由度 ν の χ² -変量 χ² から、

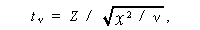
(2.59)

を作ると、自由度 ν の χ² -分布になることを利用すると

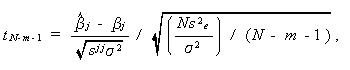
(2.60)

は、自由度 ν =N -m -1 の t -分布に従うことがわかる。ここで、s^jj は、X^t_m X_m の逆行列の第（j ,j ）要素である。これは (2.57)式 より明らか。 　 (2.60)式は、(2.58)式に注意すると、

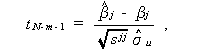
(2.61)

と書ける。したがって、帰無仮説

(2.62) の検定には、 (2.63) を計算し、 (2.64) ならば、H0 を棄却すればよい。ここで、tN -m -1 ()は、 自由度 ν =N -m -1 の t -分布の上側( )%点の値である。

ここで、通常 (2.62) 式の β_{j 0} は、ゼロとして検定が行われることに、 まず注意しよう。

　 しかし、この式の形から明らかなように、このゼロのケースはあくまでも特別の 場合であり、この検定は非常に一般的な形をしていることにも注意が必要である。 実は、この一般的な場合の検定は、例えば２つの集団での個々の偏回帰係数が等しい と言えるかどうかの検定にも直ちに適用できる。後の適用例のところでふれるように、 SAS の reg プロシジャには、これを簡単に指定できるオプションが備わっている ので、必要であればこの種の検定も簡単に実行させることができる。