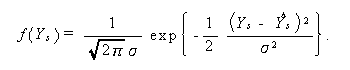
|
(2.65) |
重回帰分析モデルの母数の1つ σ2 の推定について最後に述べる。重回帰 モデルは、誤差変動、したがって基準変数 y に正規性を仮定しているので、モデル の母数の推定結果は最小二乗法による結果と最尤法による結果は一致するが、ここ では、AIC(Akaike's Information Criterion)との関係で、最尤法による推定 方法について述べる。
まず、(2.1)式のモデルから、Yの(確率)密度関数は、
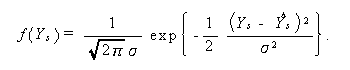
|
(2.65) |
故に尤度関数は、
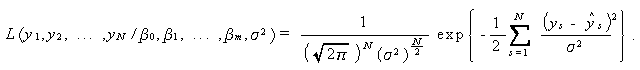
|
(2.66) |
そこで、
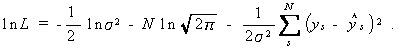
|
(2.67) |
したがって、ln L を最大にするような β0 ,β1 , ... , βn 、σ2 は、
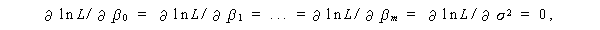
|
(2.68) |
を満たす。これより、
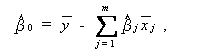
|
(2.69) |
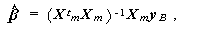
|
(2.70) |
|
(2.67)式の右辺の σ2 に 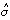 2 を代入すると、
2 を代入すると、
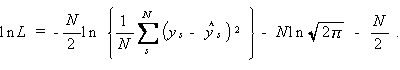
|
(2.72) |
上式で、yに無関係な項を省略し、改めて ln L を書き下すと、
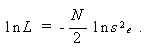
|
(2.73) |
ここで、p をパラメーター数とする赤池の AIC
| AIC = -2ln L + 2p , | (2.74) |
に、(2.73)式を代入すると、この場合、m +2個の母数のうち、σ2 、 β0 の分を2つ差し引いて、
|
AIC は、 モデル選択(model selection)の立場から作られた指標であり、 同一のデータセットに対して、複数のモデルを考え、AIC 最小のモデルを 選択する。この考え方を、(2.75)式を用いて重回帰分析の場合に応用することも できよう。この応用は、基準変数に効いている変数が m 個のうちどれにあたるか という変数選択の問題を考える時起こる。