2.6節 残差分析の必要性
これまで何節かに亘り重回帰分析の理論にふれてきたが、これを実際のデータに
適用するに際しては、他の統計的方法と同様分析の前提を得られたデータが満たして
いるかどうかを検討してから結論を下すべきであろう。
そこで、2.1 節で述べた重回帰分析モデルの前提とその骨子をここで復習のため
まとめてみると、つぎのようになる。まず、モデルの大前提は、(2.1) 式の誤差項
E1 , E2 , ... , EN が、平均 0、分散 σ2 の正規分布母集団
からの互いに独立なサンプルである、というものである。
もしこの仮定が正しいとすれば、標本重相関係数 R から計算される
量 F = (R2 /m )/(1 - R2 )/(N - m - 1) は、母重相関係数がゼロ(もしくは、
偏回帰係数がすべてゼロ)なる帰無仮説のもとで、自由度 m 及び N - m -1 なる
F -分布に従う。また、同じくうえの仮定が正しいとすれば、偏回帰係数の推定
値から計算される量 t(省略)は、母偏回帰係数がゼロ(もしくは定数)なる
帰無仮説のもとで、自由度 N - m -1 なる t -分布に従う。
重回帰分析では、データがこれらの仮定を満たしているかどうかを検討するのが
慎重な態度であろう。とりわけ、誤差項の解析は
残差分析 (residual analysis) として知られており(例えば、Belsley,
Kuh, & Welsch, 1980; Draper & Smith, 1966; 奥野ら、1972; 柳井・高木編著、
1989)、誤差分布
が果たして正規分布母集団からのサンプルと言えるかどうか、誤差間に相関がない
か、誤差分散が一定と言えるか、 外れ値 (outlier) がないかどうか、など
の検討を行うとよい。
例えば 正規性の検討は、正規確率紙へのプロットや直接的な検定の方法
があるが、SASプログラムを用いれば簡単に正規性の検定を行わせることがで
きる。また、 誤差間の相関が予想される場合には、ダービン・ワットソン
比などを計算させるとよい。外れ値の有無の検討には、各サン
プルのサンプル番号を横に取り、誤差推定値を縦軸に取り、単純にプロットしたり、
てこ比 (leverage) 等を計算し出力させるとよい。てこ比は、つぎのように
定義される:
ここで、基準変数を (2.8) 式の yB のように平均を引いたものとせず、
(2.2) 式の左辺のような y で与えられるものとすると、y の予測値
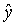 は、(2.11) 式とよく似た形の
は、(2.11) 式とよく似た形の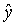 = X
= X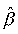 と表される。また、
と表される。また、 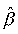 も (2.12) 式とよく似た形の
も (2.12) 式とよく似た形の
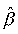 = (XtX )-1 Xty と書ける。
この時、Xt X は正則で
あるものとする。これらより、
= (XtX )-1 Xty と書ける。
この時、Xt X は正則で
あるものとする。これらより、 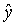 = H y が成り立つ。ここで、
H = X ( Xt X )-1 Xt
である。この行列 H の対角要素
h ii = h i = xi (Xt X )-1 xti
のうち値の大きなものを
てこ比と呼ぶ。hi の値は常に 0 ≦ hi ≦ 1 である。Belsley, Kuh,
and Welsch (1980) は、hi ≧ 2q / N なる hi を持つ観測値(サンプル)
をてこ比点 (leverage point) と呼ぶ。 q は回帰係数の数であり、一般的には
β0 も含むので q =m +1(予測変数数プラス1)である。
もっとも、重回帰分析におけるデータの正規性からのズレに対する F -検定量
の頑健性については、古くから知られている。例えば、Box & Watson (1962) は、
F -統計量は正規分布に近い分布の場合には頑健であることを示している。しかし
同時に、予測変数のうち1つか2つが他と大きさが大きく異なる時には、非正規性
に対する F -検定量の頑健性は失われること、なども報告している。すなわち、
F -検定は正規性からのズレに対して手放しで頑健であるわけではないことに注意
が必要である。
= H y が成り立つ。ここで、
H = X ( Xt X )-1 Xt
である。この行列 H の対角要素
h ii = h i = xi (Xt X )-1 xti
のうち値の大きなものを
てこ比と呼ぶ。hi の値は常に 0 ≦ hi ≦ 1 である。Belsley, Kuh,
and Welsch (1980) は、hi ≧ 2q / N なる hi を持つ観測値(サンプル)
をてこ比点 (leverage point) と呼ぶ。 q は回帰係数の数であり、一般的には
β0 も含むので q =m +1(予測変数数プラス1)である。
もっとも、重回帰分析におけるデータの正規性からのズレに対する F -検定量
の頑健性については、古くから知られている。例えば、Box & Watson (1962) は、
F -統計量は正規分布に近い分布の場合には頑健であることを示している。しかし
同時に、予測変数のうち1つか2つが他と大きさが大きく異なる時には、非正規性
に対する F -検定量の頑健性は失われること、なども報告している。すなわち、
F -検定は正規性からのズレに対して手放しで頑健であるわけではないことに注意
が必要である。
上述の誤差分析とりわけ外れ値等に対処するためのもう1つの方法として最近数
理統計学の分野で注目を集めているのが、重回帰分析に ロバスト推定 (robust
estimation) を用いるものである(例えば、Huber, 1981; Staudte & Sheather,
1990)。一般に、外れ値が予想されるようなデータの場合、共分散行列や偏回帰
係数の推定にも大きな影響が及ぶことがわかっている。そこで、この方法では、
外れ値を見つけて最初から除くのではなく、外れ値による影響を小さくするような
一種の重みを導入し偏回帰係数を推定する 。Huber の古典的 M-推定量
(M-estimators) は、その1つの例である。
最後に、重回帰分析では上述のような外れ値等の問題をクリアできたとしても、
なお問題となる点の1つは予測的妥当性であろう。すなわち、一回の標本から重
相関係数が統計的に有意であったとしても、そのことは必ずしも新たな同種のサ
ンプルに対して得られた重回帰方程式を用いての基準変数の予測が予測的妥当性
を持つことを十分に保証するわけではない。その点を検討する問題は、つぎの節
でふれるように、古くから
交差妥当性 (cross-validation) の問題として知られている(例えば、McNemar,
1969)。
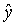 は、(2.11) 式とよく似た形の
は、(2.11) 式とよく似た形の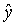 = X
= X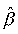 と表される。また、
と表される。また、 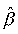 も (2.12) 式とよく似た形の
も (2.12) 式とよく似た形の
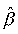 = (XtX )-1 Xty と書ける。
この時、Xt X は正則で
あるものとする。これらより、
= (XtX )-1 Xty と書ける。
この時、Xt X は正則で
あるものとする。これらより、 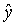 = H y が成り立つ。ここで、
H = X ( Xt X )-1 Xt
である。この行列 H の対角要素
h ii = h i = xi (Xt X )-1 xti
のうち値の大きなものを
てこ比と呼ぶ。hi の値は常に 0 ≦ hi ≦ 1 である。Belsley, Kuh,
and Welsch (1980) は、hi ≧ 2q / N なる hi を持つ観測値(サンプル)
をてこ比点 (leverage point) と呼ぶ。 q は回帰係数の数であり、一般的には
β0 も含むので q =m +1(予測変数数プラス1)である。
もっとも、重回帰分析におけるデータの正規性からのズレに対する F -検定量
の頑健性については、古くから知られている。例えば、Box & Watson (1962) は、
F -統計量は正規分布に近い分布の場合には頑健であることを示している。しかし
同時に、予測変数のうち1つか2つが他と大きさが大きく異なる時には、非正規性
に対する F -検定量の頑健性は失われること、なども報告している。すなわち、
F -検定は正規性からのズレに対して手放しで頑健であるわけではないことに注意
が必要である。
= H y が成り立つ。ここで、
H = X ( Xt X )-1 Xt
である。この行列 H の対角要素
h ii = h i = xi (Xt X )-1 xti
のうち値の大きなものを
てこ比と呼ぶ。hi の値は常に 0 ≦ hi ≦ 1 である。Belsley, Kuh,
and Welsch (1980) は、hi ≧ 2q / N なる hi を持つ観測値(サンプル)
をてこ比点 (leverage point) と呼ぶ。 q は回帰係数の数であり、一般的には
β0 も含むので q =m +1(予測変数数プラス1)である。
もっとも、重回帰分析におけるデータの正規性からのズレに対する F -検定量
の頑健性については、古くから知られている。例えば、Box & Watson (1962) は、
F -統計量は正規分布に近い分布の場合には頑健であることを示している。しかし
同時に、予測変数のうち1つか2つが他と大きさが大きく異なる時には、非正規性
に対する F -検定量の頑健性は失われること、なども報告している。すなわち、
F -検定は正規性からのズレに対して手放しで頑健であるわけではないことに注意
が必要である。