|
因子分析は、もともとビネーに始まる知能検査の開発の歴史と共に、知能の
数量的把握の方法として発展したもので、スピアマン(Spearman, C., 1904)の2
因子説(Spearman's two-factor theory)、ガーネット(Garnett, J.C.M., 1919-20)
に始まりサーストン(Thurstone, L.L., 1931)がうち立てた多因子説(multiple
factor theory)、ホルテンガー(Holzinger, K.J., 1937)の双因子説(bi-factor
theory)などが知られている。
これらの理論は、いわば、現象の背後にある因子の数や構造についての大枠を
示してはいるが、必ずしもデータを手にして、どのようにそれらの因子や構造を
抽出するかを答えるものではない。
これらのうち多因子説が、最も一般的な因子分析モデルであり、その因子数や
因子の構造をデータから推定する方法(解法)が、これまで数多く開発されてき
た。
これらの方法は、推定される因子相互が直交しているか否かで、大きく 直交解 (orthogonal solutions)と 斜交解(oblique solutions)に分けられる。直交解の1つとして良く知られているのが 主因子解(principal factor solution)(Hotelling,
1933) である。一方、斜交解には、オブリマックス解(oblimax solution)(Pinzka & Saunders, 1954)、オブリミン解(oblimin solution)(Carroll, 1960)、クオティミン解(quartimin solution)(Carroll, 1953)、プロマックス解 (promax solution) (Hendrickson & White, 1964)、多群解(multiple-group solution)(Holznger, 1944; Thurstone, 1945) などがある。
因子分析は、他の多変量解析と異なり、もともと心理学者が提唱した記述統計的
方法であったが、ローレイ(Lawley,D.N., 1940)やヤレスコフ(J\"oreskog,K.G.,
1981)らによる 最尤解(maximum likelihood solutions)が可能となり、現在では
推測統計的方法として発展している。
サーストンの多因子説に基づく多因子模型は、つぎのように表される。
|
ここで、Z i j は、第 i サンプルの第 j 変数の値で、平均0、分散1に
基準化されたもの、aj 1, ... , a j r ,b j は、
因子の係数 又は
負荷量(loadings)と呼ばれる未知数、
F i 1 ,F i 2 , ... , F ir , G i j
は、第iサンプルの因子の値又は因子得点(factor scores)と呼ばれる。
すなわち、多因子模型では、個々の変数の値は、r個(r \leq m )の
共通因子(common factors)と、1組の 独自因子(unique factor)の
ウエイトづけ合計点で表される。
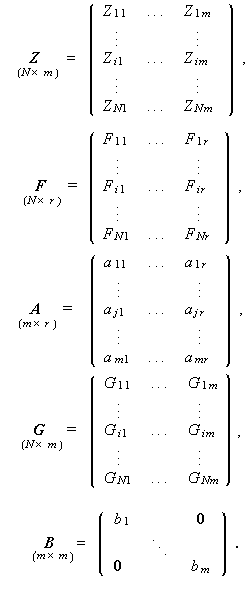
(3.1)式は、行列表現では、つぎのように表される。
|
ここで、

|