| { | Z 1 = | a 11 F 1 + a 12 F 2 + | ... | + a 1r F r + b 1 G 1 , | |
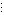
|
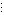
|
(3.3) | |||
| Z m = | a m1 F 1 + a m2 F 2 + | ... | + a mr F r + b m G m , | ||
(3.1)式の添字 i を省略し、添字 j ごとに当式を書き下すと、
| { | Z 1 = | a 11 F 1 + a 12 F 2 + | ... | + a 1r F r + b 1 G 1 , | |
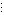
|
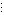
|
(3.3) | |||
| Z m = | a m1 F 1 + a m2 F 2 + | ... | + a mr F r + b m G m , | ||
のようになる。この一組の式は因子パターン(factor pattern)あるいは単に
パターン(pattern)と呼ばれる。なお狭義には、(3.2)式の行列 A を、因子
パターンと呼ぶ。行列 A は、別名、因子行列(factor matrix)とも呼ばれ
る。
既に述べたように、因子分析モデルの解法は、因子相互が直交しているか否か
で、直交解と斜交解に大別できるが、(3.1)あるいは(3.2)式の多因子模型は、そ
の両方を含み、因子相互には、つぎの弱い制約のみを課すに過ぎない。
|
ここで、φj k は、第 j 因子と第 k 因子相互の相関係数を表わす。直交
解とは、すべての φj k がゼロの場合の模型の解である。
因子分析では、因子相互の相関関係ばかりではなく、もとの変数(テストバッテ
リー)と因子との相関関係の情報も、因子の解釈の時などに必要である。これは
一般に、因子構造(factor structure)あるいは単に、構造(structure)と呼ば
れる。
因子構造には2種類あり、1つはもとの変数と共通因子との相関 P であり、
狭義の因子構造と呼ばれる。他方は、もとの変数と独自因子との相関 D である。
(3.2)、(3.4)、(3.5)、(3.6)式から、
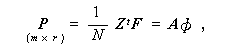
| (3.7) |
また、
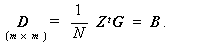
| (3.8) |