|
(3.1)式の多因子模型から明らかなように、因子分析では、各変数の分散((3.1)
式では、これは1に基準化されている)、共通因子によるものと独自因子による
ものから成り立つ。
具体的には、(3.1)式の行列表現(3.2)式と、その仮定についての(3.4)~(3.6) 式を用いると、つぎのように簡単に表現できる。すなわち、
|
もし、共通因子相互が直交すれば、
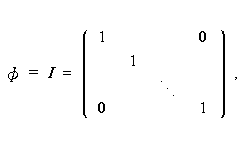
|
(3.10) |
なので、この時は、
| R = AA t + BB t . | (3.11) |
(3.11)式の第 j 行 j 列は、第 j 変数相互の相関係数を表わすので、1であるが、 これは、第 j 変数の分散でもある。このことに注意すれば、
| s 2 j = 1 = h 2 j + b 2 j . | (3.12) |
ここで、
| h 2 j = a 2 j 1 + a 2 j 2 + ... + a 2 j r . | (3.13) |
この h 2 j は、第 j 変数の
共通性(communality)と呼ばれ、第 j 変数の
分散に占める共通因子の寄与を表わす。
これに対して、b 2 j は 独自性(
uniqueness)と呼ばれ、同じく独自因子の寄与を表わす。
(3.1)式から明らかなように、模型の右辺はすべて未知なので、われわれは観測
されたデータから因子数 r のみならず、共通性(あるいは独自性)なども推定し
なければならない。
まず、共通性の下限および上限については、つぎの結果が知られている。ここで、 R 2 j は、第 j 変数をそれ以外の m -1変数で説明したときの 重相関係数 (multiple correlation coefficient)の二乗であり、r j j は第 j 変数の 信頼性(reliability)である。
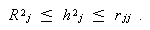
|
(3.14) |
すなわち、共通性( h 2 j )は、(第 j 変数の)信頼性( r j j )を上廻る
ことはなく、 SMC(Squared multiple correlation coefficient)を下廻ること
もない。
前者すなわち上限については、(3.1)式の独自性の部分をさらに特殊因子(
specific factor)と誤差因子(error factor)に分解し、誤差分散と信頼性との
間の関係( e 2 j = 1 - r j j )に注意すれば容易に証明できる。後者すなわち
下限については、Dwyer(1939)の証明がある。
つぎに、観測データから共通性を推定するための方法として従来からよく知られた
ものを列挙すると、
| (1) | 相関行列の第 j 列(あるいは j 行)の要素の絶対値 最大のものを、h 2 j の推定値とする。 |
| (2) | SMC( R 2 j )を h 2 j の推定値とする。 |
| (3) | 反復近似(iterative approximation)による方法。 |
これらのうち、(1) の方法はThurstone派により用いられたもので、最も簡単な
ものであるが、変数数が小さいと、良い推定値を与えないといわれる。