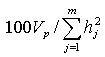
|
(3.17) |
直交解の場合、共通因子の各々の、全変数の分散に占める 総寄与(total contribution)は、
| V p = a 2 1p + a 2 2p + ... + a 2 mp . | (3.15) |
1 これは通常、 因子寄与(contribution of factor V p )と書かれる。もち ろん pは、1から r に亘る。したがって、 寄与率 あるいは 共通性のパー セント(Per cent of communality)は、
| 100 V p / m , | (3.16) |
または、
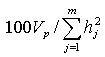
|
(3.17) |
で表わされる。前者は、全分散に占める第 p 共通因子の寄与率であり、後者は、 共通性に占める第 p 因子の寄与率である。
最後に、この節までの因子分析に関する基礎知識を、藤井の筆跡データの YG 12尺度について の因子分析結果を用いてまとめるとつぎのようになる:
データ(ここでは、藤井の筆跡データ50名分)のうちの YG 12尺度得点を用いて、因子分析を 行うには、まず12の尺度間の相関行列を計算する必要がある。つぎに、相関行列の対角要素には 各尺度の共通性の初期推定値を何らかの方法で計算して入れることが必要である。そのためには、 3.1.3 節の最後の方にリストアップした3種の方法のいずれかを用いるとよい。これにより、 3.2.1 節の (3.19) 式に示す(縮退)相関行列が得られる。この行列の固有値を計算することに より、われわれは12尺度で測られる YG 性格検査の因子の数を推定することができる。教科書的 には、固有値が1以上の数が推定された共通因子の数である。以下は、藤井の筆跡データの場合 の縮退相関行列の固有値を大きい順に出力したものである。つぎの例は、初期値の推定方法のう ち、3.1.3 節の最後の3種の方法の第1番目、すなわち縮退相関行列の各列(または各行)の最大 値(の絶対値)を当てる方法を用いたものである:
Eigenvalues of the Reduced Correlation Matrix: Total = 7.12598836 Average = 0.59383236
Eigenvalue Difference Proportion Cumulative
1 4.80478315 3.19498018 0.6743 0.6743
2 1.60980298 0.89550601 0.2259 0.9002
3 0.71429696 0.47712223 0.1002 1.0004
4 0.23717473 0.07489073 0.0333 1.0337
5 0.16228400 0.07415303 0.0228 1.0565
6 0.08813097 0.03802531 0.0124 1.0688
7 0.05010566 0.06556896 0.0070 1.0759
8 -.01546329 0.03201960 -0.0022 1.0737
9 -.04748289 0.05415711 -0.0067 1.0670
10 -.10164000 0.06577734 -0.0143 1.0528
11 -.16741734 0.04116925 -0.0235 1.0293
12 -.20858658 -0.0293 1.0000
2 factors will be retained by the NFACTOR criterion.
|
うえの出力結果から、YG 性格検査は2因子からなると推定できる。
うえの12個の固有値を、縦軸に固有値の値、横軸に固有値の番号を取り、プロットしたものは スクリープロットと呼ばれ、この例ではつぎのようになる:
固有値のスクリープロット
|
|
|
5 +
| 1
|
|
|
|
|
4 +
|
|
|
|
|
|
3 +
E |
i |
g |
e |
n |
v |
a 2 +
l |
u |
e | 2
s |
|
|
1 +
|
| 3
|
|
| 4
| 5 6
0 + 7 8 9
| 0 1 2
|
|
|
|
|
-1 +
|
|
------------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-----------
0 1 2 3 4 5 6 7 8 9 10 11 12
Number
|
因子数を推定したならば、つぎに われわれは通常主因子法を用いて(因子数を指定した因子分析を行い)初期解を得る。これが、つぎの ような因子パターンである。
Factor Pattern
Factor1 Factor2
yg1 depression 0.75564 0.23388
yg2 cyclic tendency 0.69186 0.36614
yg3 infereiority complex 0.79712 -0.12053
yg4 neurosis 0.86149 0.12262
yg5 objectivity 0.71311 0.29762
yg6 cooperativeness 0.48640 0.40548
yg7 aggressiveness 0.08732 0.49735
yg8 general activity -0.60901 0.40596
yg9 rhathymia -0.19828 0.44268
yg10 thinking extroversion -0.56407 -0.19020
yg11 ascendance -0.69753 0.49372
yg12 social extroversion -0.64022 0.50043
|
ただし、このようにして得られる因子パターンは、必ずしも心理学的に解釈しにくい。そこで、われわれ は心理学的有意味性を確保するために、1つの方法としてバリマックス回転を行う。この方法は、うえの ような因子パターンの構成要素である因子負荷量を各軸の座標値とみなし、サーストンの単純構造の原理に 基づいて座標系を回転し、もっとも有意味と思われる位置で回転を止めることにより、最終的な因子パターン を計算する。そのようにして得られた因子パターンは、回転後の因子パターンと呼ばれる。
Rotated Factor Pattern
Factor1 Factor2
yg1 depression 0.75952 -0.22096
yg2 cyclic tendency 0.77913 -0.07544
yg3 infereiority complex 0.59895 -0.53962
yg4 neurosis 0.78659 -0.37213
yg5 objectivity 0.75912 -0.14434
yg6 cooperativeness 0.62930 0.07055
yg7 aggressiveness 0.34680 0.36703
yg8 general activity -0.28473 0.67426
yg9 rhathymia 0.07831 0.47869
yg10 thinking extroversion -0.57557 0.15191
yg11 ascendance -0.31029 0.79626
yg12 social extroversion -0.25876 0.77030
|
うえの結果から、各因子を解釈・命名することができる。第1因子は、YG 12尺度の前半の情緒安定性 に関わる項目であるので、例えば「情緒安定性因子」と名づけることができよう。一方、第2因子は、後半の 向性や活動性に関わる項目であるので、例えば「向性・活動性因子」と名づけることができよう。
Variance Explained by Each Factor
Factor1 Factor2
3.8356367 2.5789494
|
うえの結果は、YG 性格検査の因子分析における2因子の因子寄与を示す。例えば、この2つの値の和で それぞれの因子寄与の値を割り100倍したものは、因子寄与率の中の「共通因子のパーセント」と呼ばれる。
Final Communality Estimates: Total = 6.414586
yg1 yg2 yg3 yg4 yg5 yg6
0.62569216 0.61272954 0.64992424 0.75720230 0.59709358 0.40100099
yg7 yg8 yg9 yg10 yg11 yg12
0.25498481 0.53570171 0.23527944 0.35435325 0.73031220 0.66031192
|
最後に出力されるのは、各尺度の最終的な共通性の推定値である。うえを見ると、YG9 や YG 7 は共通性が 他の項目に比べるとかなり低いあたいになっており、YG 12尺度の中ではかなり異質なものといえよう。