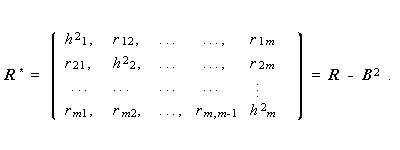
|
(3.19) |
従来からよく用いられる多因子模型の解法は、主因子法による主因子解( principal-factor solution)である。主因子法は、因子寄与 V p が、つぎの 条件下で最大になるように因子パターン A を決定する方法である:
|
行列表現では、
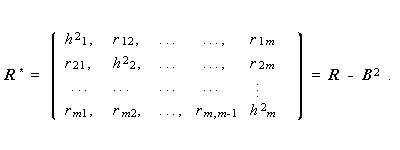
|
(3.19) |
主因子解は、結局つぎの 固有値問題(eigenvalue problem)を解くことに よって得られる。
|
ここで、 固有値(eigenvalue)λp に対する 固有ベクトル (eigenvector) a p は、つぎのように長さを定めるものとする。
|
すなわち、主因子解における固有値の値は、各々の因子の因子寄与になるように
してあるので、因子数の推定のための1つのめやすとなる。通常、固有値は大きい
順に計算し、それが1前後で急に小さくなる手前までを推定因子数とする。この
点についてのより詳細な議論については、後の 3.4.1 節で SAS による因子分析
の適用例を示しながら行うので参照されたい。
主因子解は、因子寄与が、与えられた縮退相関行列 R * のもとで最大なも
のから幾つかを選ぶもので、得られた因子パターン A は、この意味では一意
的(unique)である。
一方、心理学者は、従来から得られた因子パターンの各々の因子の解釈に際して
の、各因子の 心理学的有意味性(psychological meaningfulness)を問題とし
てきた。
というのは、一般に何らかの方法で1つの因子パターン(直交解)が得られたと する。すなわち
| R * = R - BB t = AA t . | (3.22) |
この時、われわれは A を用いて各変数を r 次元直交座標系の中の1 点として表わすとすれば、座標系の直交回転
|
のための直交変換行列(orthogonal transformation matrix)U を任意に 選んで、
|
とすることができる。
簡単に言えば、座標軸の任意の直交回転に対して、点間の構造―すなわち R *
で表わされる変数相互の相関関係―は不変なのである。このことは、因子の非決定性
(indeterminacy)の問題として知られている。
そのために、われわれは、何らかの方法で手にした因子負荷行列すなわち因子パター
ンを r 次元の座標値とみて、何らかの基準を用いて座標回転を行い、因子の心理学的
有意味性を追求することになる。
そのための1つの基準を提唱したのがサーストン(Thurstone,L.L., 1947)で、
サーストンの単純構造の原理(Thurstone's principles of simple structure)
と呼ばれる。原理は5つの基準から成り立っている。
サーストンの原理を目指した回転基準の中で、最もよく使われているのが、カイ
ザー(Kaiser,H.F, 1958)による バリマックス法(the varimax method)である。
バリマックス法において最大化されるべき関数は (正規)バリマックス基準 (normal varimax criterion)と呼ばれ、つぎの式で定義される。
|
ここで、 c j p は、第 j 変数の第 p 因子に対する因子負荷量である。
この式から、バリマックス回転は、共通性 h 2 j で基準化された因子負荷量の
二乗の分散(variance)を最大(maxmize)化するような回転であることがわかる。
最後に、YG 性格検査データ(藤井データの一部)を用いた、因子分析の一連の手順により出力される主要な SAS による情報をまとめると、つぎのようである:
最初、12尺度間の相関行列を計算し、共通性の項の最後で述べた3つの方法のうちの1つの方法 (ここでは、それらのうちの (1) の方法、すなわち相関行列の各列の絶対値最大なもの(の絶対値)を 相関行列の対応する対角要素とする方法)により、共通性の初期推定を求め、相関行列の対角要素とした。 これが、主因子解とバリマックス回転の項で述べた縮退相関行列である。つぎの出力は、そのすべての 固有値をリストした SAS の出力結果である。
Eigenvalues of the Reduced Correlation Matrix: Total = 7.12598836 Average = 0.59383236
Eigenvalue Difference Proportion Cumulative
1 4.80478315 3.19498018 0.6743 0.6743
2 1.60980298 0.89550601 0.2259 0.9002
3 0.71429696 0.47712223 0.1002 1.0004
4 0.23717473 0.07489073 0.0333 1.0337
5 0.16228400 0.07415303 0.0228 1.0565
6 0.08813097 0.03802531 0.0124 1.0688
7 0.05010566 0.06556896 0.0070 1.0759
8 -.01546329 0.03201960 -0.0022 1.0737
9 -.04748289 0.05415711 -0.0067 1.0670
10 -.10164000 0.06577734 -0.0143 1.0528
11 -.16741734 0.04116925 -0.0235 1.0293
12 -.20858658 -0.0293 1.0000
2 factors will be retained by the NFACTOR criterion.
|
うえの固有値の値から、正確には1以上の固有値の数から、YG 性格検査の12尺度はおよそ2つの共 通因子で説明できることがわかる。これより、つぎの主因子法による主因子解は2因子を指定して行う。
以下の結果が、主因子法による最初の因子パターンであり、回転前の因子パターンと呼ばれる。この 解は、主因子解とバリマックス回転の項で述べたように、必ずしも心理学的には解釈しやすい結果には なっていない。そこで、それらが心理学的に解釈しやすいものにするために、サーストンの単純構造の 原理にかなうように因子軸を(バリマックス)回転するのが、つぎの項である。
Factor Pattern
Factor1 Factor2
yg1 depression 0.75564 0.23388
yg2 cyclic tendency 0.69186 0.36614
yg3 infereiority complex 0.79712 -0.12053
yg4 neurosis 0.86149 0.12262
yg5 objectivity 0.71311 0.29762
yg6 cooperativeness 0.48640 0.40548
yg7 aggressiveness 0.08732 0.49735
yg8 general activity -0.60901 0.40596
yg9 rhathymia -0.19828 0.44268
yg10 thinking extroversion -0.56407 -0.19020
yg11 ascendance -0.69753 0.49372
yg12 social extroversion -0.64022 0.50043
|
以下の結果が、バリマックス回転後の12尺度の因子パターンと、最終的な因子寄与及び共通性の推定 値である。ここで、主因子解は直交因子を仮定しているので、得られた因子パターンの各要素である因子 負荷量は、各因子ともとの尺度や項目間の相関係数に等しいことを用いて、われわれは各因子がどの尺度 群と相関が高いかを見ることにより、各因子の解釈と命名を行うことができる。
Rotated Factor Pattern
Factor1 Factor2
yg1 depression 0.75952 -0.22096
yg2 cyclic tendency 0.77913 -0.07544
yg3 infereiority complex 0.59895 -0.53962
yg4 neurosis 0.78659 -0.37213
yg5 objectivity 0.75912 -0.14434
yg6 cooperativeness 0.62930 0.07055
yg7 aggressiveness 0.34680 0.36703
yg8 general activity -0.28473 0.67426
yg9 rhathymia 0.07831 0.47869
yg10 thinking extroversion -0.57557 0.15191
yg11 ascendance -0.31029 0.79626
yg12 social extroversion -0.25876 0.77030
Variance Explained by Each Factor
Factor1 Factor2
3.8356367 2.5789494
Final Communality Estimates: Total = 6.414586
yg1 yg2 yg3 yg4 yg5 yg6
0.62569216 0.61272954 0.64992424 0.75720230 0.59709358 0.40100099
yg7 yg8 yg9 yg10 yg11 yg12
0.25498481 0.53570171 0.23527944 0.35435325 0.73031220 0.66031192
|