３.２.２節 固有値問題としての各種因子解

　前節で、主因子解が(3.20)式で与えられる固有値問題の解として得られること を述べた。

　主因子解はそこで述べたように、因子寄与が、与えられた共通性と変数相互の相関 関係の条件下で、最大になるような因子解を求めることによって得られる。

　これに対して、目的は異なるが結果として主因子解と類似した固有値問題に帰着 される方法が幾つか知られている。それらは、正準（カノニカル）因子分析（ canonical factor analysis）、アルファ因子分析（alpha factor analysis）、 主成分分析（principal component analysis）による、正準因子解、アルファ 因子解、主成分である。

　まず、正準因子分析では、もとの変数の組と、多因子模型(3.2)式の共通因子成分 FA t による m 変数の組との間の相関係数を最大にするような合成変量を 因子として求める。ここで、

(3.26)

と置けば、行列 Y が、共通因子成分による m 変数の組を表わす。

　一般に２組の変数のそれぞれの合成変量間の相関が最大になるとき、それは 正準相関係数（canonical correlation coefficient）と呼ばれ、そのような合成 変量を求める方法は、 正準相関分析（canonical correlation analysis）と 呼ばれるために、うえの方法に対してそのような名前が付けられている。

　この場合、正準相関係数は、次の２つの合成変量（重みづけ合計点）間の 相関係数を最大化するものとして求められる。

(3.27)
(3.28)

f と g の相関係数 ρ( f , g ) は、結局、

(3.29)

となり、これを最大にする v 、 w は、

(3.30)

v = B -1 u , (3.31)
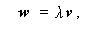
(3.32)
(3.33)
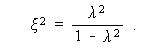
(3.34)

として与えられる。

　ここで、因子負荷量は、共通成分から作られる合成変量 f すなわち因子とも との変数との相関で与えられるので、

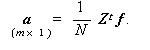
(3.35)

(3.35)式は、(3.26)、(3.27)、(3.31)式などを用いると、

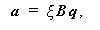
(3.36)
(3.37)

となる。因子パターン A は結局

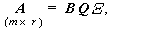
(3.38)

で与えられる。

　ここで、

(3.39)
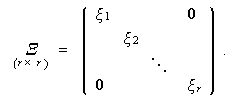
(3.40)

(3.40)式の対角行列の要素は、(3.30)式の固有値問題の解の固有値の平方根を r 個並べたものである。

　一方、アルファ因子分析では、共通因子成分から作られる合成変量としての 因子の信頼性（reliability）を最大にするようなウエイトづけを求める。

　共通因子成分から作られる合成変量の α 係数は

(3.41)

で与えられる。ここで、

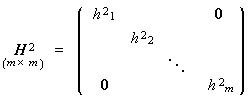
(3.42)
(3.43)

　そこで、(3.41) 式のアルファ係数を最大にするようなウエイトづけ w は、

w t ( R - BB t ) w , (3.44)

が、

w t H 2 w , (3.45)

を一定とした時最大となるようにして求められる。この解は、結局

(3.46)

なる固有値問題の解を得ることに帰着される。

ここで、

p = H w . (3.47)

　因子負荷量は、正準因子分析の場合と同様にして、

(3.48)

で与えられる。ここで、

(3.49)
(3.50)
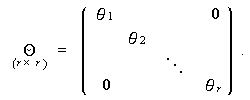
(3.51)

　アルファ因子分析を提案したカイザー（Kaiser,H.F）とキャフリー（Caffrey,J.) は、因子数をアルファ係数が正に対応する因子のみ認めるという基準を提案し ている。このことは、(3.46)式の固有値 θ2 のうち１より大なものに対応 する因子数をもって、推定因子数とすることにあたる。

　最後に主成分分析では、もとの変数の合成量

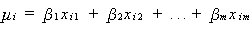
(3.52)

の分散をウエイトの大きさを一定とした条件下で最大にするように求める。行列 表現では、μ は、

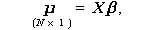
(3.53)

ここで、

(3.54)

合成変量の分散 S 2 u は、

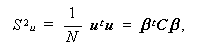
(3.55)

と書ける。ここで、

(3.56)

は、共分散行列である。これを

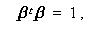
(3.57)

のもとで最大化すると、

(3.58)

なる固有値問題に帰着される。

　 ここで、もし、データがすべて平均０分散１に基準化されていれば、

(3.59)

となる。

　 正準因子分析、アルファ因子分析、主成分分析、主因子解の固有値問題を比較 すると、結局固有値問題における行列を、

(1) 主成分分析では、
R ,
(2) 主因子解では
R - BB t ,
(3) 正準因子分解では、
B -1 ( R - BB t ) B -1 ,
(4) アルファ因子分析では、
H -1 ( R - BB t ) H -1 ,

のように取るということになる。

　 うえの方法のうち、主成分分析を除くすべての方法で、共通性の推定が不可欠で ある点に注意したい。一般的には、 1.1.3 で述べた３つの方法のいづれかを用い て、共通性の推定を行うが、正準およびアルファ因子分析では、独自性及び共通 性を逐次近似により推定しながら解を求める。(3.12)式から、共通性が推定されれ ば独自性は求まるが、一般的に独自性は共通性に比べて小さいことが多いので、 正準因子分析では、 B -1 の計算ができなくなる可能性が、アルファ因子 分析に比べて大である。