|
因子分析の中心的課題は、複数尺度(項目)により測定された当該現象(知能、
性格等)に関する情報から、尺度間の相関行列を計算し、複数の尺度で測られた
情報の背後にある基本的次元(因子)を抽出し命名することにある。
したがって、分析の第1段階は、相関行列 R から、直交解の場合には因子
パターン A を、斜交解の場合にはさらに因子間相関行列 φ を推定し、
狭義の因子構造としての、もとの変数と共通因子との相関行列 P を(3.7)式
により計算し、因子の命名を行う。
しかし、一般的に言って、因子分析も、因子の命名だけに終るのであれば、
科学的研究の段階としては、単なる分類の域を出ないことになる。
さらに、1.1.5で述べたように、因子分析では、もともと因子の非決定性が
存在し、何らかの方法で得られた因子解も、あくまでも1つの分類に過ぎない。
この弱点を考慮すると、われわれは得られた因子の各々の、たとえば予測的
妥当性(predictive validity)を検討するとか、基準変数(criterion variable)
としての妥当性などを検討することが望まれる。これらを行うには、因子分析の
第2段階としての因子得点 F の推定が必要となる。
因子得点は、複数のものさし(尺度)相互の重なりの情報を整理した後の少数
の新たなものさしと考えられる各因子上での個人差得点と考えることができるので、
これらを推定することにより、因子分析に用いた変数(尺度)以外の定性・定量
変数との間の関連性の有無の検討を行える。
たとえば、知能の規定因の分析を目的とする研究であれば、まず知能検査の
テストバッテリーの因子分析を行い、因子得点まで計算し、抽出された各因子の
因子得点を基準変数とみなし、その規定因を予測ないしは説明変数とみたてての
重回帰分析や数量化 I 類を行えばよい。もちろん、知能そのものを予測変数
にみたてる研究も可能であろう。
因子得点の推定法としては、従来からいろいろな方法が提案されている(Harman,
1967,芝,1972)が、ここでは、それらのうちで代表的な2つの方法を紹介する。
(1) 独自性最小化による推定
この方法は、(3.2)式の GB t の部分を最小にする推定法であり、 その時の因子得点 F は、つぎの最小二乗問題の解として推定される。
|
これより、F の最小二乗推定
 は、A t の擬逆行列
(pseudo-inverse)( A t )+ を用いて、
は、A t の擬逆行列
(pseudo-inverse)( A t )+ を用いて、
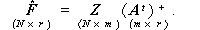
| (3.61) |
ここで、( A t )+ は、$\displaystyle{\mathop{\mbA^t}_{(r\times m)}}$ の階数(rank)が r であることに注意すると、
| ( A t )+ = ( A t ) t ( A t ( A t ) t ) -1 . | (3.62) |
そこで、
|
このように、独自性を最小にするような因子得点の推定値は、基準化された
データ行列 Z と因子パターンAから行列演算により簡単に計算できる。
(2) 完全推定法
この方法は、(2.61)式の ( A t )+ のかわりに、未知のウエイト $\displaystyle{\mathop{\mbW}_{(m\times r)}}$ を考える方法である。 言い換えれば、この方法による因子得点は、もとのデータ(尺度)から 作られる合成変量により説明されるという立場にたって得られる。すなわち
|
これは要素表現すれば、
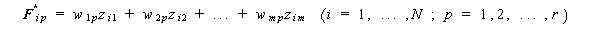
| (3.65) |
となり、r 本の重回帰方程式(multiple regnession epuation)を考えていること に等しい。この解は、擬逆行列 Z+ を用いて、
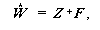
| (3.66) |
ここで、 Z N\times m の階数は m として、

| (3.67) |
に注意すると、
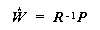
| (3.68) |
したがって、
|
直交因子の場合、(3.69)式は、
|
この場合、因子得点は、基準化されたデータ行列 Z 、因子パターン A 及び相関行列 R の行列演算により計算できることになる。
OBS Factor1 Factor2 Factor3 Factor4 Factor5
1 0.31437 1.65348 0.61042 -1.48477 -0.58720
2 -0.01072 -0.71286 -0.06003 0.09055 1.05729
3 0.24824 -0.54324 -1.22068 -1.04111 0.49309
4 -1.09862 -0.17071 0.71697 -1.16737 -0.48835
5 -0.60635 -1.00952 -2.12104 -1.19266 -0.37534
6 -1.15287 1.38427 0.45401 0.32688 0.19814
7 0.34053 -0.99533 -1.57051 -0.76516 -1.65557
8 0.97236 0.67307 0.21504 0.57579 0.89287
9 1.81321 1.04621 0.04310 -0.11434 1.78126
10 -0.49436 -0.83521 0.26804 0.03021 -1.47843
11 -1.92801 0.82557 -0.05721 -0.50636 0.08321
12 1.17105 -0.84077 -1.32078 -0.05043 0.97049
13 -0.90249 0.81256 -0.71317 2.08837 0.83877
14 0.35266 -0.48361 -0.99979 -1.02470 -1.35042
15 -0.22791 -1.90038 -0.40872 0.02418 0.80752
16 -1.82901 0.73663 -0.07252 0.53208 -0.70696
17 -1.34098 0.91832 1.55373 0.17650 -0.30631
18 0.24082 0.85683 -0.78034 0.82084 -0.28108
19 0.36817 -2.27016 0.75913 -0.95807 0.83394
20 -0.71399 -2.10817 1.64975 1.03427 -0.63377
21 -0.98429 -0.02576 0.41530 0.33211 0.64777
22 1.64814 0.37409 1.19217 0.03978 -0.00403
23 -0.29179 1.66147 0.94163 0.50349 -0.78734
24 1.09542 1.48350 -0.11404 -2.21799 0.63042
25 -0.01857 1.24013 0.72080 0.32937 0.16360
26 -0.52906 -1.15124 -1.65710 0.86464 0.67362
27 -0.12682 0.42263 -0.05133 0.81813 -0.00355
28 1.73384 0.38860 1.56244 0.84480 -1.21528
29 -0.79388 0.27090 0.58202 -1.07769 1.69014
30 1.36724 -0.23551 -0.07758 0.30985 -0.59374
31 0.33642 1.23631 -2.07901 -1.10685 -1.96512
32 -0.35435 -0.59047 -1.00451 1.85612 -0.35877
33 -1.84819 -1.17495 1.00354 -1.39361 0.26290
34 0.50160 0.68645 -1.03575 1.35442 0.17357
35 0.16720 -0.80991 -0.22204 -0.42930 -1.38168
36 0.45325 0.13618 -0.19034 -1.30099 0.17766
37 -1.91811 -0.72627 0.94435 -0.00390 0.36189
38 1.14149 0.66118 0.02112 -0.05246 0.81144
39 0.13055 -1.66769 0.52714 0.55300 -0.55523
40 -0.40968 0.55313 -1.76253 1.44988 0.69547
41 0.76392 0.24025 0.02992 -0.77194 0.19814
42 0.78738 -0.70883 0.29014 0.05761 -0.23920
43 0.43512 -0.48142 0.91985 -0.37952 1.62132
44 -0.03122 0.43478 -0.27360 1.46220 -0.31213
45 0.98780 -0.37643 0.27728 -0.09984 -0.99867
46 -0.34577 0.09133 0.88119 -1.02514 0.49319
47 1.07728 -0.61368 -0.00930 0.52595 1.51542
48 1.38026 -0.29970 1.00020 1.53477 -0.84111
49 -0.17231 0.62303 1.22571 0.14187 -1.59692
50 -1.69897 1.32093 -1.00311 -0.51349 0.64310
|