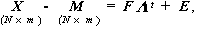
| (3.71) |
これまで述べてきた因子パターン A や因子得点 F の推定の方法は、
あくまでも記述レベルのものであった。そこでは、(3.1)式の左辺のデータは、
たまたま手にした特定のデータであり、右辺も通常の未知数でしかなく、
データから未知数を推定するに過ぎなかった。
一般に、このようなデータから、得られた因子について何らかの統計的推測を
行うことには無理がある。これに対して、得られたデータが、ある母集団からの
無作為標本とみなされるならば、データから、母集団に関する未知数（パラメー
ター）についての推論が可能になる。
因子分析における 最尤解（maximum likelihood solution）は、(3.1)式に確率
変動を導入し、多因子模型の未知数に関する推測を行う１つの方法である。
ここで、(3.1)式に対して確率変動を導入する方法は、ローレイ（Lawley,1940,
1941）に遡ることができる。
最尤解は、 共分散構造（covariance structure）を前提とするので、(3.2)式 の左辺 Z のかわりに、データを各変数の標準偏差で基準化しないものを 用いる。すなわち
|
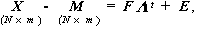
| (3.71) |
あるいは、
|
ここで、
|
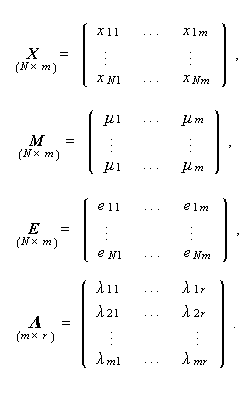
(3.72)式は、ベクトル表現では、
|
ここで、
|
(3.2)式と(3.72)式を比較すると、独自因子に関する項が、(3.72)式では
誤差項になっていること、因子パターン A が(3.72)式では、 Λ
になっていることがわかる。後者は、(3.2)式の Z が、(3.72)式では、
X - M になっていることによる。
ローレイの最初の論文では（Lawley,1940）、 f i と e i は共に
多変量正規分布に従う変量模型が提案された。一方、次の年の論文（Lawley,
1941）では、 e i のみが多変量正規分布に従う母数模型も提案された。
変量模型の場合、因子得点はモデル上確定できないのに対して、母数模型の
場合にはある条件下で定数（サンプルごとに異なる）として推定可能となる。
因子分析における変量模型では、次の２つの確率変動を仮定する。すなわち、
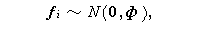
| (3.74) |
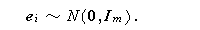
| (3.75) |
この時、(3.73)式により、
この時、共通因子数 r の多因子模型(3.71)式の仮定のもとでの母共分散行列
（population covariance matrix）は、
ここで、
ここで、一般性を失うことなく、φ = I として、
したがって、因子分析の最尤解は、平均 μ 母共分散行列 Σ
が(3.79)式の構造を持つような母集団からの標本 x 1 , x 2 , ... ,
x N の尤度を最大にするような μ 、Λ 、psi; を求める
問題になる。ここで、N 個の標本の尤度 L は、
これに対して、(3.79)式の構造を仮定しない場合に N (μ , Σ)
に従う母集団からの標本 x 1 ,x 2 , ... ,x N の尤度を最大にする
ような μ , Σ の最尤推定量
を、μ 、Σ でそれぞれ偏微分してゼロと置くことにより得られる。
ここで、
と置く時、つぎの関係
なる関係がある (Anderson, 1984,p.62.) ことに注意すると、
(3.81)式は、
(3.84)式をそれぞれ μ 、Σ で偏微分しゼロと置くと、
が得られる (Anderson, 1984, p.62-63.) 。
よく知られているように、
である（
そこで、母共分散行列 Σ の不偏推定量としては、つぎの標本共分散
行列（Sample covariance matrix）S が用いられる。
(3.90)式の S 又は(3.82)式の A の分布は、ウィッシャート分布
（the Wishart distribution）と呼ばれ、次の確率密度を持つ（Wishart,1928）：
ここで、
(2.91)式の密度は、 w ( A | Σ , n ) と、又対応する分布は
W ( Σ , n ) と表わされる。この時、S の分布は、W (\frac1n
Σ ,n ) となり、S の密度は、
ここで、 c は、 Σ に無関係な定数である。
因子分析における最尤解の導出を、テキストによっては、S の尤度を最大に
する Λ 、ψ を求めることに帰着させているが（たとえば、芝,
1972）、因子数の検定のための尤度比検定における整合性を持たせるには、アンダー
ソン（Anderson,1984）に従って、因子数 r の仮定のもとで、平均 μ 、
Σ = ΛΛ t + ψなる構造をもつ母集団からの N
個の標本 x 1 , x 2 , ... , x N
の尤度を最大にするような μ 、
Λ 、ψ を求める問題に帰着させる。
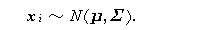
(3.76)
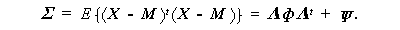
(3.77)
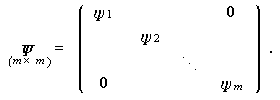
(3.78)
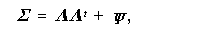
(3.79)
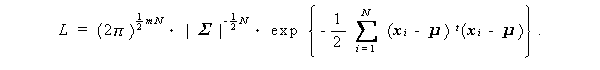
(3.80)
,
は、
(3.80)式の対数尤度
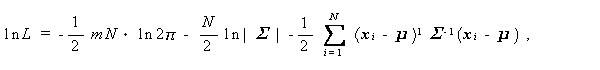
(3.81)
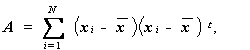
(3.82)
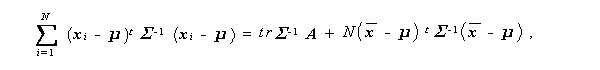
(3.83)
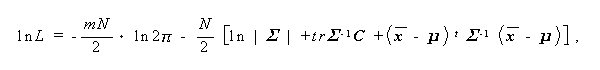
(3.84)
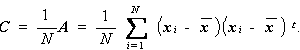
(3.85)
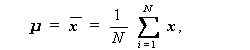
(3.86)
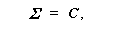
(3.87)
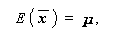
(3.88)
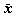は μ の不偏推定量）が、
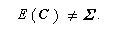
(3.89)
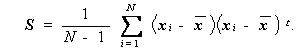
(3.90)
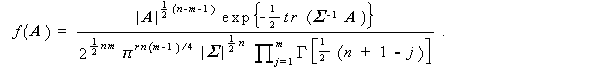
(3.91)
n = N - 1 .
(3.92)
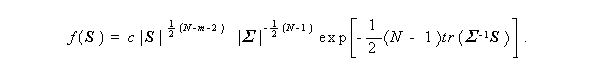
(3.93)
