３.３.２節　最尤解の反復解法

　 最尤解を得るために、(3.80)式の対数尤度(3.84)式の右辺を μ、Λ 、ψ の最尤推定量（maximum likelihood estimators）が得られる。

　 まず、μ の推定量 は、 $ \partial \, \ln L / \partial μ = \0 $ より

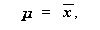
(3.94)

が得られるので、

(3.95)

　 つぎに、(3.94)式が成り立つときは、対数尤度(3.84)式は、

(3.96)

となるので、

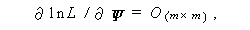
(3.97)

より、行列式の微分及びつぎの形のトレースの微 分 (Magnus & Neudecker, 1988, p.178)

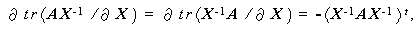
(3.98)

に注意し、最後に ψ が対角行列であることに注意すると、

(3.99)

　 ここで、一般の正方行列 H についての diag H とは、行列 H の対角要素を表わす。したがって上式は、 Σ ^-1 の対角 要素が、 Σ ^-1 C Σ ^-1 の対応する対角要素に等しい ことを意味する。

　 最後の Λ の推定量 については、

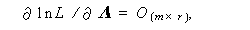
(3.100)

より、ψ の偏微分の場合と同様に、行列式の微分、トレースの微分に 注意すると、

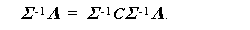
(3.101)

　 (3.101)式を変形し、(3.99)式の関係を利用すると、

(3.102)

が得られる。

　 ここで、(3.102)式で、Λ が一意的に定まるためには、

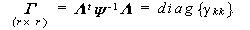
(3.103)

ここで、

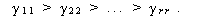
(3.104)

　 (3.103)式の条件下で、(3.102)式は行列

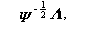
(3.105)

の各列が、行列

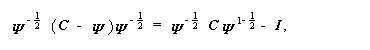
(3.106)

の固有ベクトルであり、対応する固有値が行列 Γ の対角要素であること を示している。

　 もちろん、ここで固有ベクトルは、

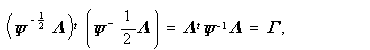
(3.107)

のように基準化されねばならない。

　 (3.102)式は、２種類の未知数行列 ψ と Λ とを同時に含むので、 反復解法により解かねばならない。 ψ と Λ の最尤推定量 、 は、反復解法により収束した結果として 与えられる。(3.102)式で与えられる因子分析の最尤解は、 C = R （相関 行列）、 ψ ^{{\frac{1}{2}}} = B とみなすと、正準因子分析と同等である ことに注意せよ。