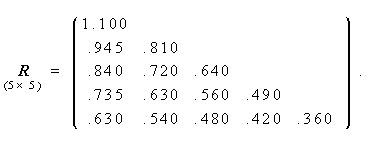
| (3.108) |
一般に因子分析の多因子模型(3.1)又は(3.2)式では(3.12)式より、共通性 h 2 j が1を越えることはない。換言すれば、 独自性 b 2 j が負になる ことはない。しかし現実には、このようなケースは起こり得るのである。これ は、ヘイウッドケース(the Heywood case)と呼ばれ、つぎのものがよく知ら れている(Harman,1967)。
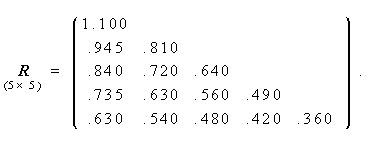
| (3.108) |
最尤解の場合にも、このようなケースが存在し得る。独自性の中に負のものが
存在する解は、 不適解(improper solution)とも呼ばれる。一方、独自性の中
にゼロのものが存在する解は、境界解(boundary solution)と呼ばれる。
ヤレスコフ(1967)は、それまでの最解を得るための反復解法を一部修正し、
固有値問題を、$\partial \ln L / \partial ψ の数値解法による最大化
($-\partial \ln L / \partial ψ の最小化)をはかりながら解く方法
を提案し、不適解の回避をねらった。
その後も、不適解に対処するための方法が数多く提案されているが、この問題は 完全に解決されているとは言えない。