３.３.４節　因子数の検定

　 因子分析に限らず、一般に最法を用いると 尤度比検定（likelihood ratio test）を用いてモデルのあてはまりの良さの検定が可能となる。

　 単純仮説（simple hypothesis）の場合、尤度比は、

(3.109)

　 ここで、分母の尤度は、尤度の無条件最大値、分子の尤度は、帰無仮説

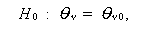
(3.110)

のもとでの条件付最大値である。

　 この時、

(3.111)

は、帰無仮説のもとで、漸近的に自由度 ν の χ² -分布に従う。ここで、 ν は自由なパラメータ数である。

　 因子分析の最尤解では、(3.109)式は、

(3.112)

　 ここで、尤度の無条件最大値 L ₁ は、(3.80)式、(3.83)式、(3.86)式、及び (3.87)式から、

(3.113)

　 これより、

(3.114)

　 これに対して、帰無仮説 H ₀ のもとでの条件付最大値 L ₀ は、

(3.115)

　 ここで、

(3.116)

　 また、

(3.117)

が成り立つので、

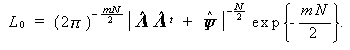
(3.118)

　 結局、これらより、

(3.119)

　 一方、

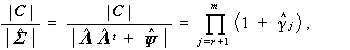
(3.120)

が成り立つので (Anderson, 1984, p.560-561.)、 (3.119)式の $\ell$ は、

(3.121)

　 ここで、 _{r +1 r +2} , ... , _m は、(3.106)式の行列の反復収束後の固有値のうち、大きい固有値を r 個除いた 残りの m - r 個である。

　 (3.111)式に、(3.121)式を代入すると、

(3.122)

　 ここで、χ ² の自由度 ν は、最尤解の変量模型の自由パラメーター の数であり、

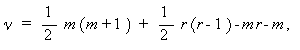
(3.123)

と計算される。ここで、右辺の各項は順に、(3.79)式の Σ の要素数、 因子の回転の自由度、(3.79)式の、Λ、ψ の要素数である。 (3.123)式を整理すると、

(3.124)

　 因子数 r は、あらかじめ未知なので、まず r = 0 又は、1 と仮定した 場合の最尤解を求め、H ₀（ r =0 又は、1 での変量模型 (3.79)式が真）を 検定し、もし H ₀ が棄却されたならば因子数を１つ増して再度最尤解を求め、 H ₀ が採択されるか ν \leq 0 すなわち、

(3.125)

となるまで、これを続ける。

　 この手続きは、しかしながら完全ではなく、不適解が得られたり、収束しなかった りすることもある。

　 バートレット（Bartlett (1950)）は、(3.122)式の χ ² の近似をよくする ために、この式の N のかわりに、

とする修正方法を提案している。

　 因子数を検定の立場からでなく、モデル選択の立場から見ると、例えば 赤池の情報量基準ＡＩＣを求め、ＡＩＣ最小の場合の変量模型を選択する。