| 4.1 はじめに |
| 4.2 対応分析の概要 |
| 4.3 判別分析の概要 |
| 4.4 対応分析・重回帰分析・判別分析の逐次的使用例 |
| 4.5 ロジスティック回帰分析の概要 |
| 4.6 判別分析・ロジスティック回帰分析の逐次的使用例 |
| 4.7 ロジスティック回帰分析による色の好悪の分析例 |
この節には、つぎの SAS プログラムのダウンロードコーナーがあります:
| 1.対応分析・重回帰分析・判別分析併用のプロ グラム例 |
| 2.判別分析のプログラム例 |
| 2. ロジスティック回帰分析のプログラム例1(比例オッズモデル) |
| 2. ロジスティック回帰分析のプログラム例2(通常の2値反応変数) |
このページは、平成30年5月9日に更新しました。
このテキストでは、多くの多変量解析の方法のうち最も基本的な2つの方法、すな
わち重回帰分析と因子分析について述べたが、多変量解析もしくはより広義には多
次元データ解析の方法にはこれら以外にも多くの方法がある。例えば、重回帰分析
における基準変数が定性的要因の場合の判別分析 (discriminant analysis)、
同じく基準変数が複数の場合の正準相関分析や多変量回帰分析、因子分析をその
特殊形として含む共分散構造分析 (covariance structure analysis) などは、
よく知られた方法である。SAS では、これらの方法はそれぞれ、discrim、cancorr、
calis、の各プロシジャにより実行できる。
また、多変量解析というより多次元データ解析というべき方法で、応用範囲の広い方法に、林の数量化の方法(あるいは、数量化理論、数量化) I、II、III、IV 類 がある。まず、数量化 I 類 は、説明変数が定性的要因の場合の重回帰分析である。数量化 II 類は、説明変数が定性的要因の場合の判別分析である。数量化 III 類は、定性的変数の場合の因子分析的方法である。数量化 IV 類は、eij 型数量化とも呼ばれ、一種の多次元尺度構成法である。これらのうち、数量化 III 類については、SAS にこれと同等の対応分析 (correspondence analysis) があり、coresp プロシジャで実行可能である。その他、1種の因子分析的方法として、クラスター分析 (cluster analysis)、多次元分類データのための対数線形モデル (log-linear model) なども有用な方法である。
また、近年数理統計学の分野で開発されてきた一般化線形モデル (generalized linear model) や、非線形混合モデル (nonlinear mixed model) 、一般化線形混合モデル (generalized linear mixed model) は、
などから、今後心理学などの社会行動科学の分野のデータ解析に多用されるであろう。これらは、SAS では、genmod、nlmixed、glimmix プロシジャにより実行できる。対数線形モデルやロジスティック回帰分析 (logistic regression) は、一般化線形モデルの先駆けとして位置づけられる。SAS では、前者は genmod プロシジャや catmod プロシジャで、後者は logistic プロシジャや genmod プロシジャでそれぞれ実行可能である。
対応分析 (the correspondence analysis) は、一言で言えば、定性的変数の組についての因子分析的方法と言える。最も単純なケースは、被験者の Yes-No 型(もしくは 0-1 型データ、あるいは2値データ)の組であり、例えば、この節の後半で取り上げる中出(1994)の例では、大学生126名に対するバウムテストに描かれた絵の特徴を94の2値データとしてコード化したもので、当該被験者がある項目の特徴を持った木を描いた場合1とコード化し、そのような特徴を持った木を描いていなければ0とコード化することにより得られたものである。その結果、各被験者のデータは、木の特徴を表す2値データの並び(プロフィール)として特徴づけられる。
2値データの場合の対応分析データの一般形は、表 4.2.1 のようになる:
| 被験者番号 | 2値データ反応 |
| 1 | δ11 , δ12 , ... , δ1m |
| 2 | δ21 , δ22 , ... , δ2m |
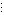 |
... |
| N | δN1 , δN2 , ... , δNm |
ここで、δij は、被験者 i の第 j 変数への反応で、Yes の(あるいはその変数の特徴を持っている)場合1、No の(あるいはその変数の特徴を持っていない)場合0、とコード化する2値反応であるものとする。対応分析では、このような反応は2値反応に限らず、各変数は多肢選択肢からなる多値反応でもよい。その場合の1つのやり方は、各変数の多値反応を当該選択肢数から成る2値反応の列に変換する方法である。この場合、もとの多肢選択肢の各選択肢は排反カテゴリーからなるものとする。言い換えれば、被験者はそれぞれの変数の複数の選択肢のうちのいずれか1つのみに反応する場合である。
2値反応のもう1つのデータ例をあげると、例えば高木 (2007) では、色彩選択の研究で、赤、黄、緑、青、紫、白、グレー、黒、オレンジの9色を提示し、まず直感で1色を選ばせ、さらに被験者が選んだ色のイメージを、26の主として形容詞からなるリストから選ばせた。ちなみに、それらは順に1.怒り、2.うれしい、3.落ち着き、4.癒し、5.大人っぽい、6.楽しい、7.セクシー、8.純粋、9.元気、10.暗い、11.かっこいい、12.明るい、13.冷静、14.ミステリアス、15.悲しい、16.自然、17.さわやか、18.やる気がある、19.情熱、20.安らぎ、21.冷たい、22.清純、23.あいまい、24.無、25.地味、26.あたたかい、であった。これらは、予備調査であらかじめ色のイメージを自由記述させた結果から、度数のある程度以上あるものを選んだ結果得られたものである。この場合、色のイメージは複数選択を可能とした。被験者152名の色のイメージ26語への反応は、152行26列の2値データであり、表 4.2.2 のようになる:
| 被験者番号 | 1.怒り | 2.うれしい | ・・・ | 25.地味 | 26.あたたかい |
|---|---|---|---|---|---|
| 1 | 0 | 1 | ・・・ | 0 | 1 |
| 2 | 1 | 0 | ・・・ | 0 | 1 |
| 3 | 0 | 0 | ・・・ | 1 | 0 |
| 4 | 1 | 1 | ・・・ | 0 | 1 |
| ・ | ・ | ・ | ・・・ | ・ | ・ |
| ・ | ・ | ・ | ・・・ | ・ | ・ |
| ・ | ・ | ・ | ・・・ | ・ | ・ |
| 151 | 0 | 0 | ・・・ | 1 | 0 |
| 152 | 0 | 0 | ・・・ | 1 | 1 |
対応分析では、このようなデータをもとに、データの内的整合性 (internal consistency) を最大化するように、被験者と項目の双方に数量化得点を付与する。この原理にもとづいた数量化については、古くは導入部で述べた林の数量化法やガットマンなどの 1940 年代の仕事(例えば、Guttman, 1941) があり、その後、ベンゼクリの対応分析 (Benzecri et al., 1973) や Nishisato の双対尺度法 (dual scaling) などがある。詳しくは、例えば西里 (1982) や Nishisato (2007) を参照されたい。
Guttman (1941) によれば、このようなデータの内的整合性を最大にするには、つぎの3つの方法がある:
ここで、1、2の方法は、それぞれ被験者得点、変数(項目)得点の相関比 (correlation ratio) を最大化する問題に、3の方法は、変数(項目)、被験者の各得点間の相関係数を最大化する問題に帰着できる。つぎに示す方法は、林の数量化 III 類の方式で、変数(項目)のそれぞれ及び被験者のそれぞれに対して(事後的に)付与される数量化得点間の相関係数を最大化する方法である:
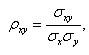
|
(4.2.1) |
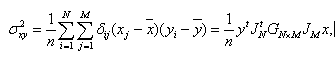
|
(4.2.2) |
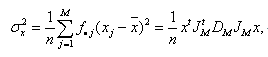
|
(4.2.3) |
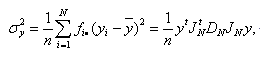
|
(4.2.4) |
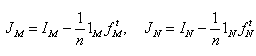
|
(4.2.5) |
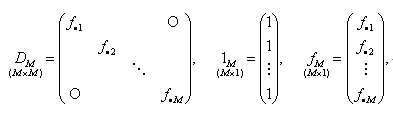
|
(4.2.6) |
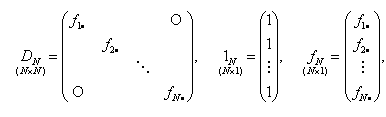
|
(4.2.7) |
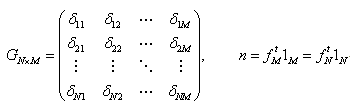
|
(4.2.8) |
σx 及び σy 一定とする条件下で、(4.2.1) 式の相関係数を最大にするような項目に対する数量化得点ベクトル x 及び被験者得点ベクトル y は、結果としてつぎの固有値問題(eigenvalue problem) を解くことに帰着できる:
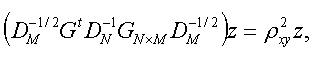
|
(4.2.9) |
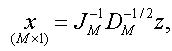
|
(4.2.10) |
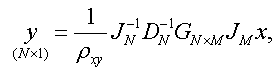
|
(4.2.11) |
ここで、(4.2.9) 式の固有値問題は、固有値問題と特異値問題の関係から、つぎの行列 F の特異値分解 (singular value decomposition)
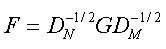
|
(4.2.12) |
と同等であることが容易に証明できる。また、このような場合、(4.2.12) 式の行列 F の 特異値 (singular value) σk と、行列 FtF、すなわち上の例では (4.2.9) 式の左辺の行列の 固有値 λk、との間には、「固有値の正の平方根は一般に特異値に等しい」という関係に注意すると、(4.2.9) 式の相関係数ρxy が (4.2.12) 式の行列 F の特異値に等しいことがわかる。実際、統計ソフト SAS では、固有値ではなく特異値を、抽出される各軸の内的整合性の指標として出力しているので、注意が必要である。もっとも、一般に (4.2.9) 式の行列の最大固有値は1であることがわかっており、これは実際の解析の場合、無意味であるので省略しないといけないが、SAS ではこのことを (4.2.12) 式の右辺の行列 Gからその分を差し引いた行列を用いることで対応している。
4.2.2. で述べた、対応分析の数理を、データの構造によって特徴づけると、つぎの表のようになる。表 4.2.3 は、表 4.2.2. のもとのデータを、対応分析により得られる各軸の被験者と項目のそれぞれに対する数量化得点により並べ替えた場合の、ある特定の軸におけるデータの反応パターン(データ構造)の架空例を示す。
| 被験者番号 | 26.地味 | 10.暗い | ・・・ | 6.楽しい | 19.やる気のある |
|---|---|---|---|---|---|
| 26 | 0 | 0 | ・・・ | 0 | 1 |
| 141 | 0 | 0 | ・・・ | 1 | 1 |
| 98 | 0 | 0 | ・・・ | 1 | 0 |
| 5 | 0 | 1 | ・・・ | 1 | 1 |
| ・ | ・ | ・ | ・・・ | ・ | ・ |
| ・ | ・ | ・ | ・・・ | ・ | ・ |
| ・ | ・ | ・ | ・・・ | ・ | ・ |
| 129 | 1 | 1 | ・・・ | 1 | 0 |
| 13 | 0 | 1 | ・・・ | 0 | 0 |
| 75 | 1 | 1 | ・・・ | 0 | 0 |
この表におけるデータの特徴は、もとの表と異なり、データとしての各被験者の1、0の反応パターンが、結果的に得られた各被験者と各項目に対する数量化得点を用いると、可能な限り右上がりの対角線に近いところに1が集中し、表の右下と左上の部分には0が多いパターンになっているといえる。また、前節での固有値の値の大きい軸ほど、このように1が対角線上の近くに集中するという特徴を示す。
うえの結果を考慮すると、われわれは、対応分析(数量化 III 類)の各軸の解釈を行うことが可能になる。すなわち、表 4.2.3 で表される特定の軸では、被験者グループ 26番、141番、98番等は、本人が直感で選んだ色に対するイメージを「地味」(項目番号26)、「暗い」(同10)とは評価せず、「楽しい」(項目番号6)、やる気のある(同19)などと評価していることがわかる。これとは対照的に、被験者グループ129番、13番、75番等は、本人が直感で選んだ色に対するイメージを「楽しい」(項目番号6)、やる気のある(同19)などとは評価せず、「地味」で「暗い」等と評価していることがわかる。つまり、両被験者群では、本人が直感で選んだ色に対するイメージ(言い換えれば、項目に対する反応パターン)が全く対照的となっているのである。言い換えれば、対応分析では一方では、項目に対する反応パターンにより被験者を少数のグループに分類していることが明らかである。
同じことは、項目についても言える。すなわち、本人が直感で選んだ色に対するイメージが「地味」で「暗い」などの項目は、特定の被験者群(この例では、26番、141番、98番など)には選択されないが、これとは対照的な特定の被験者群(この例では、129番、13番、75番など)には選択されているような特徴を持つ。つまり、対応分析では、調査に組み込んだ全項目を少数のグループに分類していることになる。対応分析(数量化 III 類)が、項目と被験者の同時分類の方法、と呼ばれるゆえんである。
いずれにせよ、上記の点を考慮すると、われわれは、項目に対する数量化得点のプラス方向の極に近い得点に対応する数項目とマイナス方向の極に近い得点に対応する数項目を選ぶことにより、各軸に対して解釈と命名を行うことが可能になる。例えば、うえの例では、この軸は、「積極性・明るさと消極性・暗さを分ける軸」のように命名できよう。
さらに、このデータでは、実際、この軸は第1軸に対応するもので、かつイメージ項目「地味」(項目番号26)、「暗い」(同10)はマイナスの極に、「楽しい」(項目番号6)、やる気のある(同19)などはプラスの極に、それぞれあたる数量化得点が付与されていた。その場合、被験者の対する数量化得点を見ると、被験者グループ(26番、141番、98番など)の得点はプラスの極の方向が対応していることになる。一方、被験者グループ(129番、13番、75番など)は、マイナスの極方向の得点が対応している。
判別分析は、基準変数が定性的変数の場合の重回帰分析と言える。重回帰分析では、基準変数は定量的変数(間隔尺度レベル以上の尺度から成る変数)であるが、これが定性的変数(名義尺度レベルの変数)になると、重回帰分析は適用できない。これに代わる方法の1つが判別分析である。
例えば、黒焦げになった遺体の男女を判別したいとする。この場合、1つの方法は、あらかじめ性別のわかっている例えば男女それぞれ100名の被験者の身体各部の長さを測定し、それぞれに最終的には最適の重みをつけ、各被験者の判別のための得点(これを判別得点という)を計算する。この得点が男女をうまく判別するような性質を持っているならば、われわれは、そこで得られた各変数への重み(これを判別ウエイトという)を、性別の不明な黒こげの遺体に適用し、遺体の判別得点を計算し、遺体の性別を判定することができる。
判別分析は、そのような最適の重み、すなわち判別ウエイトを求める方法である。もちろん、うえの例では、定性的基準変数は2値データで、例えば、1.男、2.女である。判別分析では、この定性的基準変数は必ずしも2値である必要はなく、一般に2つ以上の群でも構わない。したがって、判別分析のデータの一般形は、表 4.3.1 のようになる:
| 基準変数の値 | m 個の説明(判別)変数の値 |
| G1 | x11 , x12 , ・・・ , x1m |
| G2 | x21 , x22 , ・・・ , x2m |
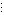 |
・・・ |
| GN | xN1 , xN2 , ・・・ , xNm |
ここで、表中 Gi は、被験者 i の属する群の番号とする。判別分析では、説明変数は原則的には、重回帰分析と同様、定量的変数であるが、ダミー化(1-0 化したもの)することにより定性的変数も組み込むことは不可能ではない。
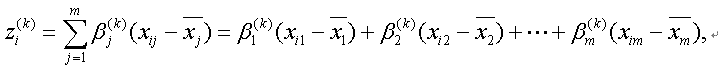
|
(4.3.1) |
と書かれる。ここで、zi(k) は、第 i サンプルの第 k 判別得点であり、基準変数としての K 個の群の判別のために用いられる。一般に、このような判別式は、群が K 個の場合、K-1 個計算できる。つまり、上の式で k=1, 2, ..., K-1 である。また、β1(k) , ... ,βm(k) は一般に、判別ウエイト と呼ばれる。
SAS では、判別ウエイトとして、構造係数の総和、群間の構造係数、プールした群内の構造係数、全標本の標準化正準相関係数、プールした群内の標準化正準相関係数、非標準化正準相関係数、の6種類を出力する。このうち、「プールした群内の標準化正準相関係数」を利用するのがよかろう。
(4.3.1) 式の判別得点の群による違いを見るためには、この判別得点の平均値を群ごとに計算し、各判別軸ごとに比較すれば、各軸が何を判別する軸であるのかを推論できる。SAS では、各群毎の判別得点の平均値は、上記6種類の判別ウエイトの直後に「正準変数における群平均」というタイトルで出力される。
この研究(中出、1994)では、A 大学2年次生126名に対してバウムテストとモーズレイ性格検査を実施し、両者の関連性を探った。バウムテストの特徴は、従来の研究を参考にして作成した94項目(右に傾いた木を描いているか、根元の膨らみを強調して描いているか、一線枝が描かれているか、地面の線を強調しているか、花を描いているか、など)を用いて判定している。
また、これらのデータは、それぞれの特徴を被験者が持った絵を描いていれば1、 描いていなければゼロとしてコード化した。以下の SAS プログラムでは、これらの 項目には baum1 から baum94 なる変数名であらかじめ永久 SAS ファイル化された ものを SAS セッション上に呼び出して使っている。また、モーズレイ性格検査の得 点は、mpi1 から mpi4 なる変数名で永久 SAS ファイルに定義された。4尺度は順に、 外向ー内向、神経症的傾向、虚偽尺度、疑問尺度である。また、この研究では、バウ ムテストの「枠付け効果」の検討も行っている。枠のありなし、の条件は、その順序 効果も見る目的で同一被験者に2カ月強の間隔で2回バウムテストを実施し、1回目 の枠ありなしをframe なる変数で、2回目のそれを frames なる変数で、それぞれ 永久 SAS ファイルで定義されている。永久 SAS ファイル名は、 sasfile.grad であ るとする。
バウムテストと性格検査の関連の検討には、まず最初に94項目の対応分析を 行い、得られた各軸の解釈を行った後、以下のプログラムで対応分析の各軸の数量化 得点とモーズレイ性格検査相互間の相関係数を計算したり、各軸の数量化得点を 基準変数とし性格検査の4尺度を説明変数とする重回帰分析を行った。また、枠あり なしの効果の検討には、その2群を判別群とし、対応分析により得られた5軸の数量 化得点を判別変数とする判別分析を用いた。
*-------------------------------------------------- October 28, 1998 -*
| sas program--crsp_ex1.sas-- |
| A sas program for executing correspondence analysis. |
| data. This data was gathered by Hiroko Nakade (1994). |
| |
| file name: $HOME/sasprog/multivar/crsp_ex1.sas |
| |
*---------------------------------------------------------------------*;
libname sasfile '$HOME/sasset/multivar';
options ps=60;
/* Delete samples whose responses are all zero or one. */
data work;
set sasfile.grad;
ndel=0;
nvar=94;
total=sum(of baum1-baum94);
if total=. or total=0 or total=nvar then do;
ndel=1; delete; end;
run;
title 'crsp for responses to, at most, 94 items';
proc corresp data=work short dimens=5 outc=coord;
var baum1-baum94;
run;
data config;
/* obs must be equal to the number of samples plus 1 */
set coord(firstobs=2 obs=127);
keep dim1-dim5;
run;
data temporal;
merge work config;
run;
title 'correlations between MPI and baum';
proc corr data=temporal;
var dim1-dim5 mpi1-mpi4;
run;
title 'multiple reg./criterion=baum dimensions';
proc reg data=temporal;
model dim1-dim5=mpi1-mpi4;
run;
title 'cross table between items, frame and frames';
proc freq data=temporal;
tables frame*frames;
run;
title 'canonical discr./criterion=frame';
proc discrim data=temporal can ncan=1;
class frame;
var dim1-dim5;
run;
|
うえのプログラムで、最初の data 文では、94項目からなるバウムの特徴の有無を表す二値項目(1又は0とコード化してあるものとする)の得点をまず一人分づつ合計し、合計点が欠側値になっているか、ゼロか、あるいは総項目数に等しい場合は、当該被験者のデータを一時的に削除するためのものである。
これが終了したら、corresp プロシジャで、94項目の二値データに対して対応分析(あるいは数量化 III 類)を施し、5軸までの項目に対する数量化得点と同被験者に対する数量化得点を求める。
つぎに、得られた5軸の被験者に対する数量化得点(これらは、dim1 から dim5 なる、ユーザ指定の変数のエリアに保存する。これは、corresp プロシジャの直後の data 文により指示してある。ここで、そこでのコメントに書いておいたように、set coord 文で指定するべき第1サンプルの番号は常にプログラムに書いたように firstobs=2 とし、obs のサンプル数は、実際の被験者数プラス1、としなければならないので、注意せよ。ここで、保存すべきデータは、config なるユーザ指定の一時ファイルである。
つぎの data 文では、うえのようにして得られた2種類のファイル work、及び configファイルを被験者(サンプル)を行として結合させるための merge 文を用いている。結合したデータの出力先は、やはりユーザ指定の一時ファイル temporal である。これが完了すると、一時ファイル temporal を用いて、以降のプログラムではつぎつぎと corr、reg、freq、discrim の各プロシジャを実行して、
などを行っている。
| crsp_ex1.sas |
判別分析と同様、基準変数(反応変数ともいう)が定性的変数の場合の重回帰分析的方法にロジスティック回帰分析がある。この方法は、もともと基準変数が二値の定性的変数のモデルとして開発されたものであるが、最近では多値でなおかつ順序尺度レベルで測定されているようなデータの場合にも拡張されている。まず、基準変数が二値の場合の伝統的なロジスティック回帰分析のデータの一般形を示すと、表 4.5.1 のようになる。ここで、B1、B2、...、BN は、各サンプルの基準変数(反応変数)の値で、二値変数を表すものとする。
| 基準変数の値 | m 個の説明変数の値 |
| B1 | x11 , x12 , ・・・ , x1m |
| B2 | x21 , x22 , ・・・ , x2m |
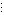 |
・・・ |
| BN | xN1 , xN2 , ・・・ , xNm |
このようなデータに対する伝統的なロジスティック回帰分析モデルは、つぎのようである。ここで、基準変数の二値データは、被験者がある群に属する時1、属さない時例えば0であるとする:
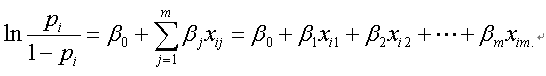
|
(4.5.1) |
ここで、式の左辺の pi は、被験者 i がある群に属する母比率(確率)であるとする。また、pi/(1-pi) は、一般にオッズ (odds) と呼ばれ、さらにその対数をとった値はロジット (logit) と呼ばれることに注意すると、ロジスティック回帰分析では、二値変数としての基準変数に対して、そのロジットが説明変数の重み付き合計点で表せるという仮定を置いていると言える。また、もともとロジスティック回帰分析では説明変数には定量的変数を仮定するが、現在では説明変数は定性的変数であっても定量的変数であってもよく、それらが混じっていてもよい。SAS では、logistic プロシジャがこれらに対応している。
ただし、もし説明変数の中に定性的変数がある場合には、このモデルは少し異なる形を取る。例えば、もし第 j 変数が定性的変数で、選択肢(カテゴリー)が nj 個から成るとする。この時、後に紹介する SAS の変換の1つである GLM コーディングのような特別な場合を除き、通常の変換では、もとの変数 xij を、nj-1 個の0、1型の二値変数 (これはダミー変数(dummy variable) と呼ばれる)の列 (Dij,1、 Dij,2、...、Dij,nj-1)に置き換える(その変換の方式に ついては、後の表 4.5.2 や表 4.5.3 を参照のこと)。ただし、表 4.5.2 の effect coding なる コーディング方式では、マイナス1を取るような場合もあり、SAS ではこのような変数をより一般 的にデザイン変数と呼んでいることに注意せよ。
その結果、(4.5.1) 式の右辺の第 j 変数の項、βjxij にあたる部分は、つぎのように書き換える必要がある:
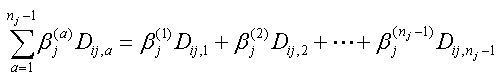
|
(4.5.2) |
また、もし2つの説明変数、xij 及び xik が共に定性的変数であり、それぞれの選択肢の数が順に nj、nk であるとし、両変数間の交互作用項をモデルに組み込みたいとしよう。また、ここで、両変数をダミー変数化したものが、順に
であるとしよう。この時、両変数が連続変数である場合の (4.5.1) 式の右辺の形 βjk xijxik に対して、つぎの形を取る:
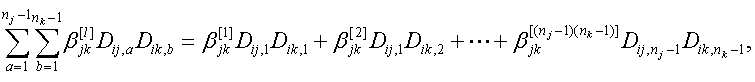
|
(4.5.3) |
ここで、(4.5.1) 式の左辺の母比率(確率) pi 、そのオッズ pi/(1-pi)、及びロジットの三者の関係については、つぎのような関係がある。すなわち、まずpiとそのオッズの関係は、pi が0から1に変化すると、そのオッズはゼロから∞へと単調増加する関係にある。さらに、オッズがゼロから∞へと単調増加すると、ロジットは -∞ から ∞ へと単調増加する関係にある。したがって、piとロジットの関係は単調増加の関係となるので、ロジットが大きくなれば母比率(確率)も大きくなり、ロジットが小さくなれば母比率も小さくなる。
このことに注意すると、つぎのことが言える。すなわち(4.5.1)式のモデルからは、
各説明変数の値の一単位分の増分に対して
|
この場合、第 j 説明変数が定性的変数で、例えば4カテゴリーから成るとする。これらのカテゴリーに対するコード値は、1、2、3、4 と自然数でも良いし、表 4.5.2 の行列の左端のように、1、2、5、7 のように飛び飛びの値でも良いし、文字変数で例えば A、B、C、D でも良い。これらのカテゴリーに対して、第 j 変数のウエイトは通常3個(カテゴリー総数マイナス1)、最大4個(カテゴリー総数)仮定できる。ここで、それらを、βj1、βj2、βj3、βj4 としよう。例えば SAS では、5種類の方法が用意されており、デザイン行列 (design matrix) を介して定義されている。また、それらは class 文のオプションの1つである param=keyword により指定できる。keyword としては、effect(デフォルト)、glm、orthpoly、poly(nomial)、ref(erence) の5つが用意されている。
例えば、effect コーディングのデザイン行列 Dは、表 4.5.2 のような4行3列の行列から成る。この場合の各カテゴリーに対するウエイトの値は、βj1、βj2、βj3を要素とする3次の列ベクトルβjを用いて、Dβj と書ける。具体的には、第1カテゴリー(1)、第2カテゴリー(2)、第3カテゴリー(5)、及び第4カテゴリー(7)に対するウエイトは、それぞれ βj1、βj2、βj3、及び -βj1-βj2-βj3 となる。
| Dj1 | Dj2 | Dj3 | |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 5 | 0 | 0 | 1 |
| 7 | -1 | -1 | -1 |
また、例えば、reference コーディングのデザイン行列は、表 4.5.3 のような4行3列の行列から成る。この場合も、ベクトルβjは effect コーディングと同一で3次である。この場合のデザイン行列は、表 4.5.3 のようである。ただし、この場合の第1カテゴリー(1)、第2カテゴリー(2)、第3カテゴリー(5)、及び第4カテゴリー(7)に対するウエイトは、それぞれ βj1、βj2、βj3、及び0となる。
| Dj1 | Dj2 | Dj3 | |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 5 | 0 | 0 | 1 |
| 7 | 0 | 0 | 0 |
結局、説明変数が定性的変数の場合には、
|
ただし、説明変数が定性的変数の場合、説明変数間の交互作用項に含まれない変数、及び交互作用項そのもの以外に限り、反応変数と当該説明変数との関連については、通常のオッズ比 (odds ratio) の概念を用いて、より正確に検討できる。ここで、オッズ比とは、一般には2つの定性的変数の関連性にかかわる概念で、もともとは、表 4.5.4 のような2×2分割表で属性 X は例えば性別(X1 は男子、X2 は女子)とし、属性 Z は例えば大学受験への成功・失敗(Z1 は成功、Z2 は失敗)とするとき、男子の成功のオッズと女子の成功のオッズの比を指す。
| Z1(成功) | Z2(失敗) | |
|---|---|---|
| X1(男子) | π1 | 1-π1 |
| X2(女子) | π2 | 1-π2 |
(4.5.4) 式は、このようにして定義されるオッズ比を示す:
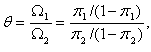
|
(4.5.4) |
(4.5.4) 式からわかるように、2つの属性が独立な場合、通常のカイ二乗統計量の定義式に注意すれば、オッズ比は1となる。このようにして定義されるオッズ比は、一般の r×s 分割表の場合にも、行、列ごとにそれぞれ2カテゴリーを取り出せば、表 4.5.4 のような表を作成できるので、計算できる。通常のロジスティック回帰分析の文脈では、これに対応するのは、r×2 分割表であり、そこでの行数は、同分析での当該定性的説明変数のカテゴリー数に対応する。また、列属性は、反応変数であり、通常のロジスティック回帰分析では二値である。
オッズ比の定義から明らかなように、当該定性的説明変数のカテゴリー数が3つ以上の場合は、理論的にはそれらの中のどの2つのカテゴリーを取り上げても、反応変数に関するオッズ比は計算できるが、通常は最後のカテゴリーを参照カテゴリーとしてオッズ比を計算する。実際、SAS では、上述のlogistic プロシジャの class 文のオプションの1つである param=keyword で、keyword として effect か reference を指定した場合、ref= の項で何も指定しないと最後のカテゴリー(last)を参照カテゴリーに指定する。ref= のオプションは、first か last である。
前節で述べたように、ロジスティック回帰分析では、反応変数と当該説明変数との関連について、オッズ比を用いて検討できる。ただし、つぎに見るように、その扱いは説明変数が定性的変数か定量的変数かにより若干異なる。
そのためには、前節で述べた各定性的説明変数のデータ入力時のコーディングと対応するウエイトパラメータとの間を関係づけるデザイン行列の取り方を適切なものにする必要がある。この場合、SAS では、前節で紹介した5種類のデザイン行列のうち、refecence コーディングを選択し、ref=last とすると(ref のデフォールト)、既に指摘したように、第 j 説明変数のカテゴリー総数を Lj とすると、Lj個のカテゴリーへのウエイトは、順にβj1, βj2, ..., βj,Lj-1, 0 となる。この時、第 j 変数への第 l(エル)カテゴリーに反応し、その他の説明変数への反応は変わらない被験者 i の (4.5.1) 式の左辺のロジット、及び第 j 変数への第 l カテゴリーに反応せず ref カテゴリーに反応し、その他の説明変数への反応は変わらない被験者 i' の同ロジット、を順に書き下すと、つぎのように書ける:
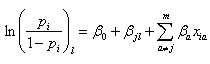
|
(4.5.5) |
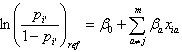
|
(4.5.6) |
これより、(4.5.7) 式、(4.5.8) 式、及び (4.5.9) 式が導ける:
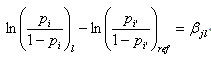
|
(4.5.7) |
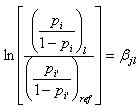
|
(4.5.8) |
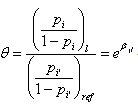
|
(4.5.9) |
(4.5.9) 式の θ は、(4.5.4) 式で定義したオッズ比であり、最右辺の値は、第 j 定性的変数の第 l カテゴリーへの reference コーディングによるウエイト βjl を指数のベキに上げたものであることがわかる。
これより、ロジスティック回帰分析における反応変数と特定の定性的変数の間に定義されるオッズ比の推定値は、ウエイトの推定値が得られれば、簡単に得られることがわかる。さらに、このことから、ロジスティック回帰分析における定性的変数の各カテゴリーの上述のような特別なデザイン行列(SAS では、reference コーディングに対応するデザイン行列)のウエイトの検定は、対応するオッズ比の検定に等しいこともわかる。ただし、この検定での有意性の有無は、定性的変数のカテゴリー数が3以上の場合は、当該変数(全体の)効果の有意性の有無とは必ずしも一致しないので、注意が必要である。
これらの結果をまとめれば、つぎのようになる。すなわち、まず
|
|
ただし、一般に、説明変数の 中に交互作用項を含むモデルを考えるときには、注意が必要である。すなわち、
|
なぜならば、交互作用が含まれる場合には、一方の変数にかかわるオッズ比は、他方の変数の値 に依存してしまうことが、つぎのように容易に証明できるからである:
まず、(4.5.1) 式のロジスティック回帰で、説明変数は2つで、xi1 は定性的変数 で n 個の選択肢から成るとする。また、これに対応する(ダミー変数を含む)デザイン変数は、第 n 選択肢が参照カテゴリーで SAS での reference coding に対応する Di1,1、...、 Di1, n-1 であるとしよう。一方、第2説明変数 xi2 は定量的変数である とする。さらに、ここで、これら2変数の単純な交互作用を含むつぎのロジスティック回帰分析モ デルを仮定するとする:
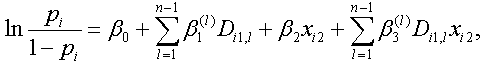
|
(4.5.10) |
つぎに、まず xi2 を固定して、第1変数の第 l (エル)カテゴリーを選択する被験者のロジットは、Di1,1 から Di1, n-1 のうち、Di1,l のみ1で、残りは0なので、つぎのように書ける:
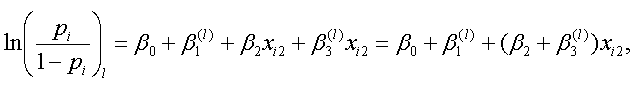
|
(4.5.11) |
一方、うえと同様、xi2 を固定し(かつ、うえの被験者 i と同一の値を取る、すなわち xi'2=xi2 とし)、第1変数はその reference カテゴリーを選択する被験者 i' のロジットは、つぎのように書ける:
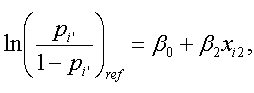
|
(4.5.12) |
これらから、被験者 i と被験者 i' のロジットの差は、つぎのように書ける:
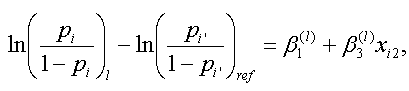
|
(4.5.13) |
つまり、この場合のオッズ比(の推定値)は、
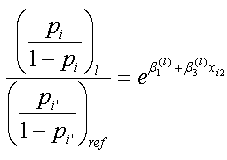
|
(4.5.14) |
明らかに、(4.5.14) 式のオッズ比、すなわち、第1変数の(参照カテゴリーに対する任意のカテゴリー (エル)への反応の)オッズ比は、右辺の内容から、交互作用項に組み込んだもう一つの変数、すなわち第2変数 xi2 に対して、被験者の反応がどのような値となるかに依存する。言い換えれば、交互作用がある場合、第1変数のオッズ比は第2変数にも依存し、一意に定めることができないことがわかる。
これと同様、第2変数のオッズ比も、第1変数にも依存し、一意に定めることができないことは、つぎのようにして簡単に確かめることができる:
今度は、xi1 を固定し(例えば、被験者は任意のカテゴリー l (エル)に反応し)、第2変数(定量的変数)の、xi2+1 の xi2 に対するオッズ比を計算すると、
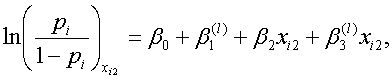
|
(4.5.15) |
及び
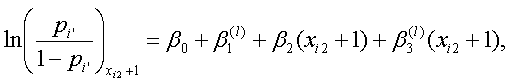
|
(4.5.16) |
これらより、
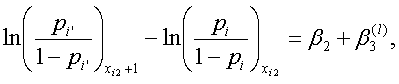
|
(4.5.17) |
これより、第2変数のオッズ比は、
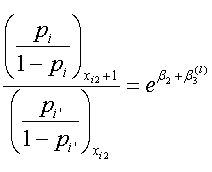
|
(4.5.18) |
つまり、この場合、第2変数 xi2 の単位あたりの増分に対するオッズ比は、交互作用項として組み込んだ他方の変数、すなわち第1変数 xi1 のどこに被験者が反応するか(上の例では、これを第 l (エル)カテゴリーとした)にも依存するので、やはり、一意的には定まらない。
前節の後半で、ロジスティック回帰分析モデルに交互作用項が含まれる場合、交互作用項 に含まれる変数のオッズ比は一意的に定まらないので検討できないことを指摘した。それで は、説明変数のうち交互作用項自身が統計的に有意な場合、交互作用項と反応変数との関連 のあり方はどのように検討すればよいのであろうか。これを行うには、条件付きオッズ 比(conditional odds ratio) の概念が必要となる。
なぜならば、この場合、反応変数を Z とし例えば定性的説明変数を X, Y とすると仮定 すると、われわれは Z, X, Y 3変数に関する3重分割表(3方向分割表、ないしは3重 クロス表)を問題にしていることになるからである。例えば、既にあげた 4.5.3 節の 表 4.5.5 が、Z と X の2×2分割表であるのに対して、Y が3カテゴリーから成り例えば 生徒の親の所得水準の高低を表すとすると、この場合 Z, X, Y のデータは3重分割表 2×2×3分割表を構成する。これを、第3番目の変数 Y のカテゴリー毎にまとめたの が、表 4.5.5、表 4.5.6、及び表4.5.7 である。これらの3表は、結局親の所得の水準ご とにまとめられた大学入試に対する成功・失敗と性別との関係を表し、親の所得水準 Yk 毎の Z と X の関連を表している。
これらの3つの表毎に計算された大学入試の成功失敗の性別による3つのオッズ比は、 ZX 条件付きオッズ比(ZX conditional odds ratios) と呼ばれる。
| Z1(成功) | Z2(失敗) | |
|---|---|---|
| X1(男子) | π111 | 1-π111 |
| X2(女子) | π211 | 1-π211 |
| Z1(成功) | Z2(失敗) | |
|---|---|---|
| X1(男子) | π112 | 1-π112 |
| X2(女子) | π212 | 1-π212 |
| Z1(成功) | Z2(失敗) | |
|---|---|---|
| X1(男子) | π113 | 1-π113 |
| X2(女子) | π213 | 1-π213 |
通常のロジスティック回帰分析では、うえに述べたように、反応変数は二値である。ここで、もし反応変数が多値であり順序尺度からなる場合、ロジスティック回帰分析を拡張することはできないであろうか。これに対応するのが、比例オッズモデル (proportional odds model) である(McCullagh, 1980)。比例オッズモデルのデータの一般形を示すと、表 4.5.8 のようになる。ここで、O1、O2、...、ON は、各サンプルの基準変数(反応変数)の値で、多値変数で順序尺度から成るとする。
| 基準変数の値 | m 個の説明変数の値 |
| O1 | x11 , x12 , ・・・ , x1m |
| O2 | x21 , x22 , ・・・ , x2m |
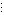 |
・・・ |
| ON | xN1 , xN2 , ・・・ , xNm |
このようなデータに対する比例オッズモデルは、つぎのようである:
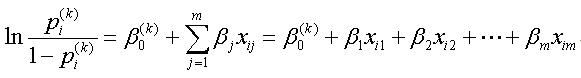
|
(4.5.19) |
ここで、(4.5.19) 式の上付き添え字 k は、反応変数のカテゴリー数を K とすると、 k=1,2, ..., K-1 に亘る。つまり、比例オッズモデルは、全部で K-1 個の方程式から 成る。k=1 の場合のモデルは、反応変数の値が第1カテゴリー以下である母比率(確率)に対応するグループか否かに関するモデルである。同様に、k=2 の場合のモデルは、反応変数の値が第2カテゴリー以下である母比率(確率)に対応するグループか否かに関するモデルである。また、下付き添え字 i は、被験者(サンプル)番号を表す。
すなわち、比例オッズモデルでは、反応変数の複数のカテゴリーに順序情報を仮定し、さらに、
|
なる仮定を置く。
SAS では、比例オッズモデルの仮定が妥当なものであるかどうかを比例オッズ条件の スコア検定 (score test) により検定することができる。ただし、Agresti (2002, p.282) によれば、この検定で同モデルの仮定が棄却されるような場合でも、 直ちにこれを捨てない方がよいとしている。これらの詳細については、Agresti (2002, pp.275-293) を参照のこと。
いずれにせよ、比例オッズモデルは、反応変数に多値の順序情報を仮定する点で、 判別分析と比べて制約の多いモデルとも言えるが、一方では厳密には順序情報を扱 うことが多い心理学等の社会行動科学の分野のデータ解析にとっては、大変魅力的 な方法と言えよう。さらに、判別分析では説明変数の効果の有無の統計的検定はで きないが、比例オッズモデルを用いれば、これが可能となる点でも魅力的である。 実際、4.6 節では、具体的なデータについて、判別分析の結果を用いて、比例オッズ モデルを構成する例を紹介する。
SAS のロジスティック回帰分析を標準的な形で指定すると、type3 分析 (type 3 analysis)
による各説明(判別)変数の基準変数に対する効きの有無の検定を Wald カイ2乗検定により
検定したり、説明変数の中に定性的変数が含まれる場合はそれらの変数の各々の複数のカテゴリ
ー(通常は、カテゴリー総数マイナス1個)に対するモデルパラメータの最尤推定値及びそれぞ
れの同推定値を Wald カイ2乗検定により検定し出力する。
しかし、このような標準的な形でのロジスティック回帰分析の指定では、それらの最尤推定値
の幾つかに関するユーザが望む仮説検定までは出力しない。これを行うためには、SAS では丁度
重回帰分析における偏回帰係数のユーザ指定による仮説検定と同様、test 文
による方法とcontrast 文による方法を用いることが可能で
あるが、ここではまず前者の方法を紹介する。この検定方法は、説明変数が連続変数の場合と
定性的(カテゴリー)変数の場合とで若干異なる:
(1)説明変数が連続変数の場合
この場合は、例えば SAS 名 dst なる連続変数の同上パラメータの最尤推定値も同連続 変数の SAS 名 rst なる連続変数の同上パラメータが等しいかどうかの検定を行いたいとすれば、 logistic プロシジャの中で分析モデルの指定の後に、つぎのように test 文を指定すればよい。 ただし、万が一両推定値のパラメータが(Wald カイ2乗検定で)有意でない場合には、以下の 検定は論理的にも意味がないと言えよう:
|
(2)説明変数が定性的(カテゴリー)変数の場合
この場合のテスト文における変数指定には、ユーザがあらかじめ指定した当該変数のコ
ード値を変数名に続けて記述する必要がある。例えば、SAS 変数名 read なる定性的変数は
2水準(0か1)から成るとすれば、第1カテゴリーに対して read0 と記述する。ここで、
既に 4.5.1 節で述べたように、カテゴリー変数については、SAS の通常の方法ではカテゴリー
変数の水準数マイナス1個のダミー変数を対応させることを思いだそう。
また、例えば説明変数が共にカテゴリー変数である場合の交互作用項の幾つかのパラメータ
に対する最尤推定値間の検定には、つぎのように記述すればよい。ここで、例えばうえの read
なるカテゴリー変数に対して、SAS 変数名 presen なる定性的変数は3水準(0、1、2)から
成るとすれば、(デフォルトとしての)最後の水準を基準としたとして、presen0 及び presen1
の2つを同検定時に使用できる。
ここで、さらに 4.5.1 節の (4.5.3) 式における上記両変数間の交互作用パラメータは、うえ
の例では nj=2、及び nk=3 なので、2つとなることに注意しよう。さ
らに、これらの2つのパラメータは、SAS のロジスティック回帰分析の出力結果の中の全パラメ
ータの「最尤推定値の分析」の項では、
|
として表記されることにも注意しよう。
この時、例えば「これら2つのパラメータの和がゼロ」なる帰無仮説の検定を行いたい とすれば、test 文としてつぎのように記述すればよい:
|
また、もし例えば「これら2つのパラメータが等しい」なる帰無仮説の検定を行いたい ならば、test 文をつぎのように記述すればよい:
|
ただし、このような定性変数間の交互作用パラメータの検定時には、注意すべき点が1つ
ある。それは既に 4.5.2 節で述べたように「
ロジスティック回帰分析モデルに交互作用項が含まれる場合、交互作用項に含まれる変数の
オッズ比は一意的には定まらない
」という点である。
実際、このことを Muto (2013) の例で見てみると次のように
なる。Muto (2013) は、ある種の文章課題に対する正答率の違いに対する読み方 (音読か黙読)
(SAS 変数名 read) と呈示方法 (一斉・文節・フロー) (SAS 変数名 presen) 並びにディジ
ットスパンテスト (digit span test; DST) (SAS 変数名 dst) 得点及びリーディングスパン
テスト (reading span test; RST) 得点 (SAS 変数名 rst) の効果を検討している。実験参加
者は 54 名で、読み方及び提示方法要因については両者の要因の水準の組合せ6条件に対し、
同参加者を無作為に割り付けている。
ここでは、このデータに対して、従属変数を正答率とし、説明変数を読み方要因、提示方法
要因と両者の交互作用、DST 及び RST 得点の5変数とするロジスティック回帰分析を行った結果を
用いて、説明する。ここでの分析のように、モデルに交互作用項が含まれる場合、交互作用項
に含まれる変数のオッズ比が一意に定まらないことは、例えば、これにかかわるカテゴリー変数
としての読み方要因及び提示方法要因のカテゴリーに対するコード値の 4.5.1 節で述べた
SAS によるコーディング方法を effect coding と reference coding とで指定を変えても、
モデルの全体的適合度や AIC などの情報量基準の値は変わらないが、各要因の効果を検討する
type3 分析による交互作用にかかわる変数(ここでは、読み方要因、提示方法要因と両者の交
互作用)の効果についてのWald カイ2乗検定結果は異なるものとなってしまうことからも
明らかである。コーディング方法を変えることによる影響は、当該ロジスティック回帰分析のパラ
メータの最尤推定値にも及ぶ。すなわち、こちらについても交互作用にかかわる変数の最尤
推定値は、コーディング方法の指定を変えると異なるものになる。また、この影響は、当該
ロジスティック回帰分析の定数項の最尤推定値にも及ぶ。
それでは、このような場合、われわれはカテゴリー変数のコーディング方法としてどれを
選択しても構わないであろうか。実は、カテゴリー変数に対するコー
ディング方法の違いは、最終的にはカテゴリー変数間の交互作用についての異なる仮説に対応
することがモデルパラメータに対する考察から明らかである。ここでは、うえの具体的
な2つのカテゴリー変数の交互作用を例にとり、コーディングの方法の違いがどのような交互
作用仮説を導くかを見てみる。
ここで、うえの文章の読み方要因を第 j 要因と表記し、黙読水準をコード値0と、音読水準を
コード値1と入力したものとする。一方、文章の呈示方法要因を第k要因と記し、その
一斉呈示水準を0、文節水準を1、フロー水準を2とコード化し入力したものとする。また、
それぞれの変数に対するSASプログラム内でのコーディングのための(ダミー変数を含む)デザ
イン変数は、第 j 変数が Dij1、第 k 変数が Dik1 及び Dik2
であるとする。この時、ロジスティック回帰分析モデルの右辺のパラメータのうち、4.5.1 節
の (4.5.3) 式で表される一般的な2つの定性的変数間の交互作用に関わる部分は、その特別な
場合として次のように表現できる:
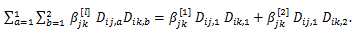
|
(4.5.20) |
a) effect coding を指定した時
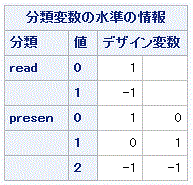
effect coding(デフォールト)を指定した場合、上記 Muto (2013) のデータの場合、デ ザイン変数は SAS のロジスティック回帰分析の出力結果の中に、つぎのように表示される:
|
表4.5.9 から、Muto data の場合のデザイン変数 Dij,1の値は、黙読条件の場合が
1で、音読条件の場合がマイナス1であること、またデザイン変数 Dik,1の値は、
一斉呈示水準、文節水準、フロー水準の順に1、0、マイナス1であり、Dik,2の値
は、同じく一斉呈示水準、文節水準、フロー水準の順に0、1、マイナス1であることがわかる。
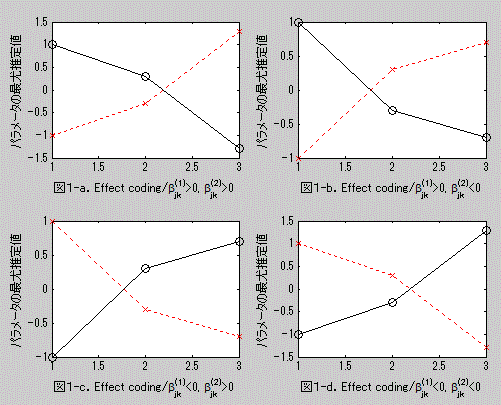
その結果、(4.5.20) 式で表される effect coding による交互作用の特徴は、βjk
[1] 及びβjk[2] の符号の正負により、図1の4つの
パターンとして表されることがわかる。すなわち、effect coding 方式では4種の交互作用仮説の
いずれか1つを仮定することに等しい。なお、この図で黒丸印の黒い実線で示した方が黙読条件、
赤×印の赤い点線で示した方が音読条件の平均である:
|
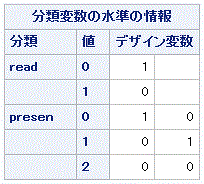
b) reference coding を指定した場合
一方、Muto (2013) のデータに対して、デザイン変数として reference coding を指定した 場合、つぎのように表示される:
|
表4.5.10 からは、Muto data の場合のデザイン変数 Dij,1の値は、黙読条件の場合が
1で、音読条件の場合が0であること、またデザイン変数 Dik,1の値は、
一斉呈示水準、文節水準、フロー水準の順に1、0、0であり、Dik,2の値
は、同じく一斉呈示水準、文節水準、フロー水準の順に0、1、0であることがわかる。
その結果、(4.5.20) 式で表される reference coding による交互作用の特徴は、βjk
[1] 及びβjk[2] の符号の正負により、つぎのような4つの
パターンとして表されることがわかる。これらは、reference coding 方式では4種の交互作用仮説
のいずれか1つを仮定することに等しい:
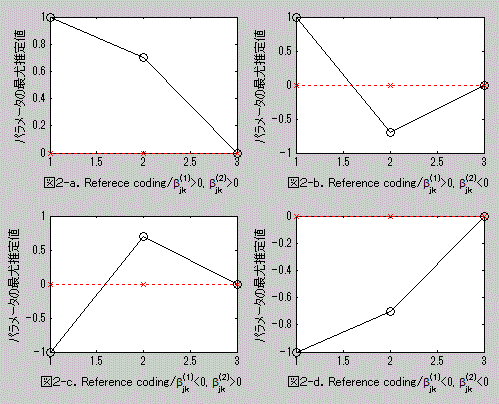
|
うえの2つのコーディングの例から明らかなように、コーディング方法の違いは交互作用の
パターンの違いを表す。また、既に指摘したように、コーディング方法の違いは定性的変数間
の交互作用関連の変数の効果やパラメータの推定値にも違いをもたらす。一方では、既に見た
ようにモデル全体の適合度は、コーディング方法を変えても不変である。
それでは、われわれはどのようにしてコーディング方法を使い分けるのがより合理的と言える
のであろうか。1つの案は、分析すべきデータの持つ特徴をより多く反映するような仮説に対
応するコーディング方法を選ぶというやり方であろう。そこで、Muto (2013) のデータで、正答率の
高さのクラスに分類する前の、実験参加者のなまのデータ(正答率そのもの)について、上記
2要因すなわち、read 要因と presen 要因の水準間の組み合わせ6条件ごとの平均を計算し
プロットした結果を見てみよう。図3は、これを示す。図中、0は音読条件を、1は黙読条件
を表す。また、横軸は文の呈示要因(sas 名、presen)で、0は一斉呈示、1は文節呈示、2は
フロー呈示のそれぞれの条件を表す:
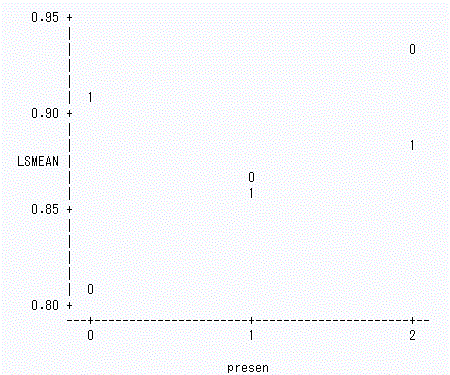
|
|
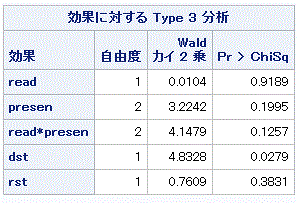
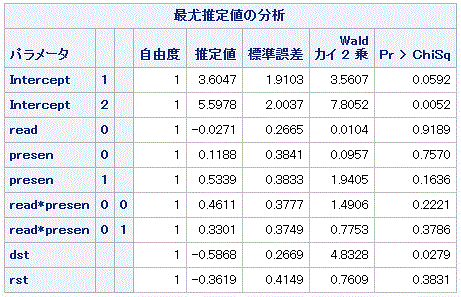
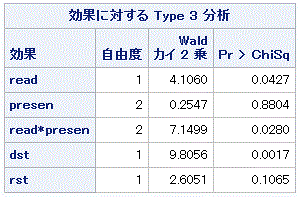
表4.5.11 から明らかなように、読み方要因と提示方法の交互作用 (read*presen) は有意とは 言えない。この結果と関連して、表 4.5.12 のモデルパラメータの交互作用にかかわる2つの パラメータの検定結果を見ると、共に有意ではないことが明らかである。
|
ここで、この節の主題に戻ると、この節での分析の主題は定性的説明変数間の交互作用項に 関するパラメータの最尤推定値に関する統計的検定問題であった。この時、Muto (2013) のデ ータのような、2つの定性的説明変数の水準が2、及び3の場合、分析の対象となるのは、 4.5.5 節の (4.5.20) 式の右辺の2つのパラメータ、 βjk[1] 及びβjk[2] に関する検定問題である。うえの表 4.5.12 では、それらの推定値は順に、0.4611 及び 0.3301 が対応する。しかしながら、この場合、そもそも表 4.5.11 で read 及び presen の交互作用は有意でなく、表 4.5.12 におけるこれら2つの推定値の有意性検定結果は、 βjk[1] もβjk[2]も共に有意でないので、 例えばこれらに関する帰無仮説 H0: βjk[1]=βjk[2]、を立てること自体、適切では ないと言えよう。
一方、Muto (201) は信号検出理論を応用し、もとの正答率のデータを変換した値(SAS 変数名 、scorate1)も算出している。図4は、このスコア値そのものを用いて、正答率の分析の場合 と同様、2つの定性的説明変数の水準の組み合わせの6条件ごとの平均をプロットし、この データでの交互作用項の特徴を図示した。この表で、文の呈示要因の第3水準(横軸での コード値は2と表示)の平均のうち、0、すなわち音読条件のみしか表示されていないが、 その理由は、1の条件すなわち黙読条件の場合のスコアが音読条件のスコアとほとんど変わらない ために表示されていないだけである。
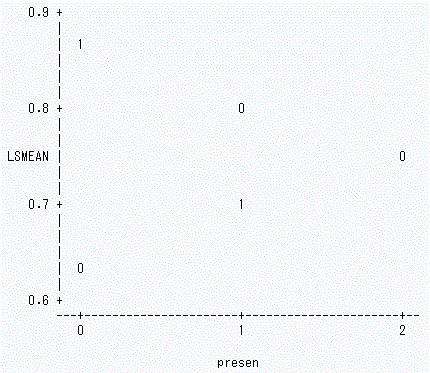
|
|
表4.5.13 から明らかなように、読み方要因と提示方法の交互作用 (read*presen) はこちら の場合、有意となった(Wald χ22 = 7.1499, p=0.0280)。この結果 と関連して、表 4.5.14 のモデルパラメータの交互作用にかかわる2つのパラメータの検定結 果を見ると、前者は有意で後者は有意な傾向があることがわかる。ちなみに、この場合の両 パラメータの推定値を見ると、βjk[1]=1.1600、 βjk[2]=-0.7354 となっている。
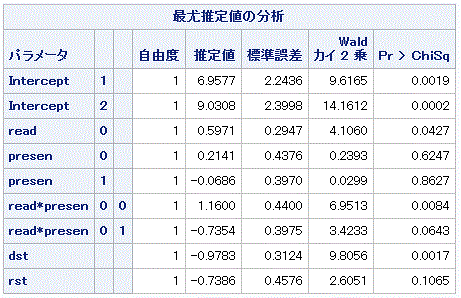
|
ここで、正答率変換後のスコアデータの場合の交互作用項の2つのパラメータは異符号とな ているので、ここでは両パラメータに関する帰無仮説としては、
を立ててみた。その結果、当該仮説は採択された(Wald χ21 = 1.1634, p=0.2808)。
4.5.1 節で述べた基準変数(あるいは反応変数)が2値の場合のロジスティック回帰分析 や、4.5.4 節で述べた比例オッズモデルとは少し異なる同回帰分析のモデルに多項ロジステ ィック回帰分析モデル (multinomial logistic regression model) がある。このモデル は、ベースライン-カテゴリーロジットモデル (baseline-category logit models) と も呼ばれる。比例オッズモデルでは、基準変数のK個のカテゴリーのそれぞれ k=1,2, ..., K-1 に対して、右辺の回帰パラメータのうちの定数項のみが異なると仮定するが、多項ロジスティ ック回帰分析モデルでは、定数項も含めたすべての回帰係数が基準変数のカテゴリーに依存す るという仮定を行う。すなわち、
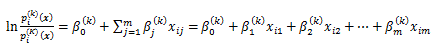
|
(4.5.21) |
このモデルは、比例オッズモデルに比べて未知パラメータ数が飛躍的に大きくなるので、モデル の適合度は、通常の検定のみ行うのではなく、例えば AIC などの情報量基準も合わせて検討 するとよいのではなかろうか。
ここでは、心理学科学生 武田 (2007) による判別分析及びロジスティック回帰分析を用いた色の好みに影響を及ぼすと考えれる「今の気分」と EPPS 性格検査の15尺度の効果の有無の検討を行った例の一部を紹介する。伝統的な判別分析では、モデルの全体的な適合度の検定は可能であるが、判別のための変数(判別変数あるいは説明変数)のそれぞれの効果の有無については、プールした群内の標準正準相関係数等の大きさをみての記述レベルでの検討までしかできない。
これに対して、近年数理統計学の分野で発展してきている一般化線形モデルのさきがけとみなされるロジスティック回帰分析、とりわけ前節で紹介した比例オッズモデル (proportional odds model)(例えば、Agresti, 2002) を用いると、判別群(あるいは反応変数)が順序尺度からなるデータに対して、モデルの適合度のみならず各説明変数の効果の有無について統計的検定が可能になり、大変便利である。例えば、SAS の logistic プロシジャを用いると、説明変数として定量的変数のみならず定性的変数も組み込むことができ、大変便利である。この例では、定性的説明変数は性別のみであり、同変数のカテゴリー数は2であるが、一般的には定性的変数のカテゴリー数は2以上あっても構わない。
まず、反応変数は、1.赤、2.黄、3.緑、4.青、5.紫、6.茶、7.白、8.グレー、9.黒、の9色であり、被験者はこれらの色の中から最も好きな色を1色選び○で囲むよう求められた。また、「今の気分」を以下の16の SD 尺度で評定するよう求められた: 1.わくわくした、2.心配した、3.恥じた、4.熱狂した、5.いらだった、6.強気な、7.機敏な、8.ぴりぴりした、9.うろたえた、10.気合の入った、11.びくびくした、12.誇らしい、13.おびえた、14.活気のある、15.苦悩した、16.きっぱりした。各尺度は、6件法(1.全く当てはまらない、2.当てはまらない、3.どちらかといえば当てはまらない、4.どちらかといえば当てはまる、5.当てはまる、6.非常によく当てはまる。最後に、被験者は EPPS 性格検査を受けた。EPPS は、225項目から成り、最終的には、1.達成、2.追従、3.秩序、4.顕示、5.自律、6.親和、7.他者認知、8.求護、9.支配、10.内罰、11.養護、12.変化、13.持久、14.異性愛、15.攻撃、の15尺度得点を算出する。
最初に、上記データに対して SAS の discrim プロシジャにより判別分析を施した。この場合の判別群は上記9色のうち反応度数が10未満の2色(茶とグレー)を除く7色への反応群で、被験者総数は134名である。一方、説明変数は、EPPS の15尺度得点、16尺度からなる「今の気分」の評定尺度得点、及び性別とした。性別は 1.男子、0.女子とした。すなわち、説明変数は定量変数が合計31変数、定性変数が1変数でダミー変数とした。判別群が7群なので、判別分析による判別軸は6本算出されるが、判別効率の1つの指標である相関比を変換した固有値の近似 F 検定によれば、第1軸のみが5%水準で統計的に有意であった (F(192, 569.97)=1.22, p=0.0397)。
そこで、各群の第1軸の判別得点の平均値をみると、1.赤(-0.939)、2.黄(-0.005)、3.緑(-1.452)、4.青(-0.082)、5.紫(0.092)、7.白(-0.140)、9.黒(1.262)、であった。これらを平均値の小さい順に並べ替えると、3.緑(-1.452)、1.赤(-0.939)、7.白(-0.140)、4.青(-0.082)、2.黄(-0.005)、5.紫(0.092)、9.黒(1.262)、の順になる。この結果から、第1軸はおよそ「緑・赤と黒を分ける軸」と言えよう。
つぎに、この第1軸の判別に効いている変数をみるために、第1軸の判別得点に対する判別ウエイトの指標として幾つか出力されるもののうち、「プールした群内の標準(化)正準相関係数」の中から相対的に値の大きい変数を抜き出すと、EPPS 12.変化(0.95)、同 14.異性愛(0.82)、同 3.秩序(0.74)、同 9.支配(0.69)、同 13.(持久)、同 10.内罰(0.62)、同 15.攻撃(0.59)、気分 15.苦悩した(0.47)、EPPS 7.他者認知(0.46)、同 5(0.45)、気分 10.気合いの入った(-0.43)、同気分 6.強気な(-0.41)、同気分 13.おびえた(-0.40)、である。この結果からは、7群の違い、とりわけ「緑・赤と黒を分ける軸には、少なくとも判別ウエイトの大きさからは、「今の気分」よりも EPPS で測られる性格特性の方がよく効いている可能性が示唆される。
さらに、判別得点の平均値の情報と各判別ないしは説明変数の判別ウエイト、とりわけ正準相関係数の符号から、例えば EPPS 12.(変化)や 14.(異性愛)と好きな色との関係は、つぎのようである。すなわち、変化や異性愛、秩序等を求める被験者は、そうでない被験者に比べて、緑や赤よりも黒を好きな色として選択する傾向があることになる。また、気合いの入った、あるいは強気な気分の場合は、そうでない場合に比べて、黒よりも緑や赤を選択する傾向があることになる。
既に指摘したように、判別分析では判別ないしは説明変数の効果の有無の検討に際して判別ウエイトの統計的検定はできない。また、判別群に対しては、群間に対しては順序情報さえ仮定していない。しかし、一旦データに判別分析を施すと、もともと名義的な判別群は結果的には各軸上で(判別得点を用いて)並べることができるので、結果的には判別群には順序情報が付与されたとみなせる。このように考え、判別分析により得られた有意な判別軸(一般には複数の可能性あり)の順序情報を利用するとすれば、われわれは各軸ごとに反応変数が順序尺度をなす場合のロジスティック回帰分析を施すことが可能である。また、これにより、我々は説明変数の効果の有無の統計的検定も可能となる。実際、上記のデータでの判別第1軸の平均値の情報により順序づけられた7色を反応変数とし、判別分析の場合と同一の説明変数により、ロジスティック回帰分析とりわけ比例オッズモデルによる分析をおこなうと、モデルの全体的な適合度の有無の尤度比カイ2乗検定の結果、同適合度は1%以上の高い水準で統計的に有意である(χ2=83.54, p<0.0001)。
また、表 4.6.1 は比例オッズモデルのパラメータの最尤推定値とそれらに対する Wald カイ2乗検定結果を示す。ここで、説明変数の項の切片1から切片6は、同モデルの反応変数(群)の順序情報にかかわるパラメータをさす。
(註)比例オッズモデルでは、順序尺度から成る特定の群以下に被験者が属する((母)比率の)ロジット (logit) を説明するものが、当該切片と説明変数の重み付き合計点であり、重み付き合計点はどの群以下に被験者が属するかの母比率のロジットにも依存しない、という仮定を置く。ここで、ロジットとは、母比率を p と書けば、ln [p/(1-p)] である。また、ln は自然対数を表す。同モデルでは、p は被験者に依存すると仮定するので、正確には、被験者を下付添え字 i で表すとすれば、 p でなく pi と書いた方がよい。p の変換式及び比例オッズモデルの形から明らかなように、ロジットと母比率とは単調増加の関係にあるので、説明変数が連続変数の場合を例に取ると、
| 説明変数 | 推定値 | | p-値
| 切片 1 | 40.54 | 4.43 | 0.0354
| 切片 2 | 42.64 | 4.89 | 0.0270
| 切片 3 | 43.43 | 5.07 | 0.0244
| 切片 4 | 44.43 | 5.29 | 0.0214
| 切片 5 | 44.91 | 5.40 | 0.0201
| 切片 6 | 45.46 | 5.53 | 0.0187
| epps1 | -0.08 | 0.59 | 0.4432
| epps2 | -0.18 | 3.51 | 0.0610
| epps3 | -0.27 | 6.40 | 0.0114
| epps4 | -0.03 | 0.09 | 0.7594
| epps5 | -0.22 | 4.27 | 0.0388
| epps6 | -0.14 | 1.93 | 0.1652
| epps7 | -0.22 | 4.66 | 0.0308
| epps8 | -0.13 | 1.89 | 0.1694
| epps9 | -0.30 | 8.31 | 0.0040
| epps10 | -0.24 | 5.94 | 0.0148
| epps11 | -0.21 | 4.41 | 0.0357
| epps12 | -0.34 | 12.82 | 0.0003
| epps13 | -0.28 | 7.11 | 0.0077
| epps14 | -0.23 | 5.43 | 0.0198
| epps15 | -0.27 | 5.70 | 0.0169
| emo1 | -0.17 | 0.90 | 0.3434
| emo2 | -0.21 | 1.42 | 0.2336
| emo3 | -0.52 | 4.47 | 0.0345
| emo4 | 0.01 | 0.00 | 0.9671
| emo5 | 0.11 | 0.29 | 0.5898
| emo6 | 0.53 | 5.44 | 0.0197
| emo7 | -0.15 | 0.42 | 0.5182
| emo8 | 0.40 | 3.05 | 0.0806
| emo9 | -0.24 | 1.67 | 0.1964
| emo10 | 0.33 | 2.87 | 0.0902
| emo11 | -0.18 | 0.50 | 0.4806
| emo12 | -0.15 | 0.35 | 0.5531
| emo13 | 0.47 | 2.53 | 0.1115
| emo14 | -0.02 | 0.01 | 0.9334
| emo15 | -0.41 | 5.93 | 0.0149
| emo16 | -0.06 | 0.15 | 0.6987
| gender | 0.52 | 4.38 | 0.0364
| |
|---|
表 4.6.1 から明らかなように、緑・赤から黒への色の好みの違いに対して、epps9、epps12 が1%以上の高い水準で、epps13 が1%水準で、epps3, 5, 7, 10, 11, 14, 15、及び emo3, 6, 15, 及び sex が5%水準で、それぞれ統計的に有意となっている。ちなみに、これらの結果は、上記同一データの同一変数による判別分析における判別ウエイト(プールした群内の標準正準相関係数)のうちでウエイトの相対的に大きい説明変数にほぼ対応している。
つぎに、うえの検定で統計的に有意であった説明変数と緑・赤から黒への色の好みの違いとの対応関係について見てみよう。例えば、epps9(支配)については、比例オッズモデルの当該変数へのウエイト(パラメータの値)の推定値の符号が、表 4.6.1 からわかるようにマイナスである点、及び epps9 の得点の大きい被験者ほど支配性が強いこと、及び反応変数の定数項(切片)パラメータの推定値の順序情報に注意すると、緑・赤方向の色を選択する可能性(確率、より正確にはそのロジット)は、支配性が強い被験者ほど小さく、支配性が弱い被験者ほど大きくなるといえる。このような特徴は、epps12(変化)、epps13(持久)、epps14(異性愛)、epps15(攻撃)等についてもいえる。また、今の気分が、emo3(恥じた)、emo15(苦悩した)時には、ウエイトの推定値の符号がマイナスなので、緑・赤方向の色を好きな色として選択する可能性が小さいことや、emo6(強気な)の場合には、当該推定値の符号がプラスであるので、緑・赤方向を好きな色として選択する可能性が大きい傾向があることがわかる。
一方、性差要因は定性的変数であるので、解釈に際して注意が必要である。(SAS の出力を見ると)性差については、パラメータの推定値は 0.5174 となっており、その符号はプラスである。ただし、出力結果を注意深く見てみると、この値は女子に対するものであることがわかる。また、出力結果の最初の方に出力されている「分類変数の水準の詳細」部を見ると、分類 sex の値 0(女子)に対応するデザイン変数の値は1であり、同じく分類 sex の値 1(男子)に対応するデザイン変数の値は -1 となっている。これらのことから、分類 sex に対するパラメータの推定値は、女子の値が 0.5174 に対して、男子の値は -0.5174 となっていることがわかる。この結果から、比例オッズモデルのモデルの形に注意すると、女子は緑・赤方向の色を選択する可能性が高く、男子はその可能性が相対的に低いといえる。
SAS の出力では、比例オッズモデルの場合、各パラメータの推定値とその検定結果を「最大尤度推定値の分析」の項で出力した後、各説明変数の「オッズ比推定値」も出力する。この値の sex の項を見ると、(0 vs 1 に対応する)オッズ比は 2.815 となっている。このことは、男子に比べた女子の緑・赤方向の色を選択する確率(正確には確率 p そのものではなく、オッズすなわち p/(1-p))が、およそ3倍と推定されることを意味している。
ここでは、前節の武田 (2007) の9色の色の好悪のデータのうち、単一色の好悪の分析を、赤色に 限ってロジスティック回帰分析により分析した例を示す。前節の同一データに対する比例オッズモデ ルの適用と異なり、ここでは「あなたの最も好きな色を以下の中(9色)から1色選び、○で囲んで 下さい」との質問に対する被験者の反応のうち、赤を選んだか否かのみを反応変数とし、その規定因 として前節の比例オッズモデルによる分析時に用いたのと同一の EPPS 15 尺度、今の気分を聞く16 尺度、及び性別の32変数を用いて、単純なロジスティック回帰分析を行った結果を示す。
まず、上記モデルの適合性の検定を尤度比カイ二乗検定により行ったところ、1%水準でモデルの適合度は統計的に有意であることがわかった(χ2(32)=56.15, p=0.0052)。そこで、つぎに赤色選択の(母)比率(より正確には、ロジット)にどの説明変数が効いているのかをモデルのパラメータの最尤推定値とそれらに対する Wald カイ二乗検定により検定した結果を示したのが表3である。
(註)ここで、この表には右端に各パラメータの指数値(特定のパラメータの推定値をβと書くと、eβの値)を示してある。この値は、説明変数が定量的変数の場合は、当該説明変数が一単位増加したときのオッズ比を、説明変数が定性的変数の場合は反応変数と当該説明変数の特定の2×2分割表に関する通常のオッズ比を表す。したがって、この表における各パラメータの推定値の Wald カイ二乗検定は、同時に、定量的説明変数の場合は、一単位増加時のオッズ比の、定性的説明変数の場合は、通常の当該2×2分割表のオッズ比の統計的検定にもあたることに注意せよ。
| 説明変数 | 推定値 | | p-値 | オッズ比
| 切片 | -24.08 | 0.46 | 0.4981 | 0.000
| epps1 | 0.28 | 2.12 | 0.1458 | 1.317
| epps2 | 0.12 | 0.45 | 0.5038 | 1.132
| epps3 | 0.07 | 0.15 | 0.7023 | 1.074
| epps4 | 0.30 | 2.03 | 0.1541 | 1.353
| epps5 | -0.09 | 0.20 | 0.6579 | 0.917
| epps6 | 0.03 | 0.03 | 0.8736 | 1.030
| epps7 | 0.16 | 0.84 | 0.3607 | 1.171
| epps8 | 0.27 | 1.92 | 0.1659 | 1.306
| epps9 | -0.01 | 0.00 | 0.9691 | 0.993
| epps10 | -0.11 | 0.37 | 0.5419 | 0.892
| epps11 | 0.23 | 1.22 | 0.2692 | 1.255
| epps12 | 0.15 | 0.74 | 0.3903 | 1.160
| epps13 | 0.08 | 0.20 | 0.6565 | 1.086
| epps14 | 0.06 | 0.11 | 0.7391 | 1.067
| epps15 | -0.01 | 0.00 | 0.9542 | 0.989
| emo1 | -0.29 | 0.65 | 0.4201 | 0.745
| emo2 | 0.26 | 0.76 | 0.3838 | 1.293
| emo3 | -1.49 | 4.02 | 0.0448 | 0.226
| emo4 | 0.80 | 3.83 | 0.0502 | 2.226
| emo5 | 0.02 | 0.01 | 0.9408 | 1.025
| emo6 | 1.16 | 5.31 | 0.0212 | 3.174
| emo7 | -0.40 | 0.73 | 0.3944 | 0.674
| emo8 | 0.32 | 0.60 | 0.4389 | 1.379
| emo9 | -0.33 | 0.75 | 0.3845 | 0.720
| emo10 | 0.11 | 0.09 | 0.7691 | 1.120
| emo11 | -1.19 | 2.76 | 0.0968 | 0.304
| emo12 | -0.72 | 2.57 | 0.1092 | 0.486
| emo13 | 1.47 | 3.73 | 0.0534 | 4.366
| emo14 | -0.01 | 0.00 | 0.9783 | 0.990
| emo15 | -0.27 | 0.72 | 0.3967 | 0.765
| emo16 | -0.47 | 1.63 | 0.2014 | 0.623
| gender | 1.48 | 2.23 | 0.1351 | 4.390
| |
|---|
表から明らかなように、赤色選択の比率には、5%水準で emo3, emo6 の2変数の効果が統計的に有意である。また、同比率には、epps1, emo4, emo11, emo12, emo13, sex の各変数の効果が有意な傾向を持つ。例えば、emo3(恥じた)のパラメータの推定値は負であり、被験者はこの得点の高いほど今の気分が "恥じた" 状態であることに注意すると、被験者は今の気分が "恥じた" 状態ならば、赤を選ぶ確率(正確には、そのロジット)が小さいことになる。言い換えれば、今の気分が恥じた状態であれば、被験者は赤は選ばない可能性が高いことになる。
一方、emo6(強気な) のパラメータの推定値は正なので、被験者は今の気分が "強気で"あるならば、赤を選ぶ可能性が高いことになる。また、性別 sex については、表中のパラメータの推定値は女子に対するものであることが、この表すなわち、「最大尤度推定値の分析」の項を見るとわかる(sex=0 であることが表示されている)。さらに、SAS 出力の最初の方に出力されている「分類変数の水準の詳細」の項を見ると、女子 (sex=0) に対するデザイン変数の値は1、男子 (sex=1) に対するデザイン変数の値は0であることがわかる。これらのことから、emo6 のパラメータの推定値は、女子が 1.48 であり、男子が 0.0 であるといえる。そこで、赤色選択の可能性は、女子の方が男子より高いといえる。ちなみに、この場合の、赤色選択の可能性の、男子に対する女子のオッズ比は、表3からわかるように、4.39 であり、女子の赤色選択の可能性(正確にはオッズ)は男子の4倍以上であるといえる。