第５章共分散構造分析

このページは、令和２年５月８日に一部変更しました。

　第３章で述べた重回帰分析では、単一の基準変数 Y _s を複数の説明変数ないしは予測変数 x ₁ , x ₂ , ... , x _m の重み付き合計点として説明するモデルを仮定した（(3.1) 式参照）。重回帰分析では、モデル式の左辺（基準変数）も右辺（複数の説明変数）も共にデータとして観測できることが前提となっている。

　つまり、重回帰分析は、ある１つの観測変数の値を（それ以外の）複数の観測変数の値でもって説明するモデル、と言うことができる。ここで、観測変数とは、観測が可能な変数 (observable variable) の意味よりも、観測された変数 (observed variable) の意味で使われることが多いが、潜在変数 (latent variable) との対比では前者の意味の方が適切であろう。なぜならば、潜在変数は少なくとも心理学の分野では、もともと直接的な観測が不可能な変数、の意味で用いられているからである。もっとも、潜在変数は原則的には直接的な観測変数にはなり得ないので、観測可能な変数と観測された変数は同義と見れるが。

　これに対して、第４章で述べた（伝統的な）因子分析では、(5.1) 式から明らかなように、観測できる変数は左辺の Z _{i j} のみであり、右辺のそれを説明する r 個の共通因子 F _{i 1} , F _{i 2} , ... , F _{i r} も各観測変数に固有な独自因子 G _{i j} も共に潜在変数である。もちろん、右辺の因子の係数（因子負荷量）は定数であり事後的に推定される。つまり、因子分析は、観測変数の値を複数の潜在変数の値でもって説明するモデルである、と言える。

　これら伝統的な２つの解析方法と比較すると、この章で述べる共分散構造分析 (analysis of covariance structures) は観測変数を（原則的には）潜在変数のみで説明するモデルなので、後者の因子分析に近いと言える。ただ、重回帰分析も（伝統的な）因子分析も共に変数間の因果関係 (causal relation) については、厳密な議論はしないのが普通である。

　それに対して、共分散構造分析では変数間の因果関係についてはっきりとした仮説を立てる点が、対照的である。共分散構造分析は、構造方程式モデル (structural equation models, 略して、SEM）と呼ばれることもある。しかし、この表現は共分散構造分析のモデルの一部（中心ではあるが）に対して使うこともあるので注意を要する。

　共分散構造分析は、伝統的な因子分析に対して、1960 年代の後半に統計学者 Jöreskog が確証（認）的因子分析 (confirmatory factor analysis) として提唱したのがその始まりである (Jöreskog, 1969)。この意味からは、伝統的な（サーストンの多因子モデルに代表される）因子分析は、探索的因子分析 (exploratory factor analysis) と呼ばれる。もっとも、analysis of covariance structures なる言葉とその概念の重要性については、既に Bock と Bargmann がその２、３年前に指摘している (Bock & Bargmann, 1966)。この辺の事情については、例えば豊田 (1992) や最近では狩野 (1997) が詳しい。

　共分散構造分析と似通ったモデルに、パス解析 (path analysis) があるが、両者には明確な相違点がある。というのは、パス解析では観測変数間の因果関係についてのみ議論する点が、共分散構造分析と異なる。

　共分散構造分析は、例えば Jöreskog and S\"orbom (1989) 自身も指摘しているように、確証的因子分析、パス解析、時系列データに対する計量経済学的モデル、重回帰分析、分散分析、多変量分散分析等や、複数の共分散行列、相関行列、回帰、因子パターン、などの等質性の検定、平均値の構造についての推定、などまで扱える有用な統計解析の方法である。

　しかし、一方ではモデルの識別性 (identifiability) の問題、同値パスモデル (equivalent pass models) の問題などが存在するし、分析の仮定そのもの、例えば「観測従属変数は潜在変数のみで説明できる」というモデルの（原則的な）仮定そのものも現象によっては妥当でない可能性もあり得よう。

　さらに、科学哲学的視点とりわけ実証主義 (positivism) の立場からは、たとえモデルの適用対象が社会・行動科学中心であるとしても、共分散分析における一種の仮説構成概念 (hypothetical construct) としての複雑な潜在変数及びその構造を仮定したり推定すること自身の妥当性、より正確にはそのような仮定の検証(verification) 可能性（確証、すなわち confirmation 可能性と異なる）や操作可能性が問われるかもしれない。また、共分散構造分析モデルの線形性は、因果モデルとしては制約が大きいと言えよう。

　とりわけ、最近では各種の共分散構造分析ソフト（AMOS、CALIS、COSAN、EQS、 LISREL、RAM、SEPATH など）も出回っており、ユーザフレンドリーになっている反面、安易な利用の危険性も増している。このような状況では、共分散構造分析適用に際してのユーザの慎重な態度と、理論の正確な把握が要求されよう。ソフトの長短については、 Kano (1997) がコンパクトにまとめている。

5.1 節共分散構造分析の概要

5.1.1 節共分散行列と共分散構造

　一般に（複数）変数の分散・共分散を行、列の形にまとめたものを統計学では共分散行列 (covariance matrix) と呼ぶ。これには、母集団のそれと標本でのそれがあり、順に Σ 、 S と書くことが多い。また、後者の標本共分散行列 S としては、サンプル数を N とすると、 N で割る場合と N - 1 で割る場合がある。S が母共分散行列 (population covariance matrix) Σ の偏りのない推定値となるためには、後者が必要である。

　いずれにせよ、常識的な意味で共分散構造と言えば、変数の分散・共分散の全体を指す Σ や S を共分散構造と言えなくない。しかし、共分散構造分析でいう "共分散構造" とは、Σ を説明する何らかのパラメータ構造 (parametric structure) を指す（例えば、Jöreskog, 1970) ので、注意が必要である。この構造を Σ と区別するために Σ ( θ ) と書くことにしよう。Σ ( θ ) は、Σ に関する１つの仮説であり、モデルとも言える。

　ここで注意すべきは、共分散構造分析でいう共分散行列 Σ は、あくまでも観測変数間に仮定されたそれであり、モデルの仮定する潜在変数間のそれではないという点である。この Σ のパラメータ構造 Σ ( θ ) は、つぎの節で述べるように観測変数と潜在変数、一部の潜在変数と他の潜在変数を結びつける方程式とその仮定によって形造られる。

5.1.2 節　共分散構造分析におけるパラメータ構造

　それでは、共分散構造分析では Σ のパラメータ構造 Σ ( θ ) は、どのように生成されると仮定するのであろうか。共分散構造分析のパラメータ構造については、現状では Jöreskog (1978) の LISREL 構造、 Bentler and Weeks (1980) の EQS 構造、 McArdle and McDonald (1984) の RAM 構造、McDonald (1985) の COSAN 構造などがあり（例えば、豊田, 1992）、それらの詳細から始めることは、必ずしも適切ではなかろう。

　そこで、ここではまず Jöreskog (1970) に従ってそのパラメータ構造を簡単に紹介することにする。まず、データ行列 X は N 行 p 列の行列で、N 人の被験者の p 個の観測変数の値を要素とする。また、X の各行は独立に分布し、それぞれはつぎの式で表される共分散行列 V ( X ) と平均ベクトル E ( X ) を持つ多変量正規分布に従うとする：

	(5.1)
	(5.2)

　すなわち、共分散構造分析の一般モデルでは、p 個の観測変数の平均、分散、及び共分散（共に複数個）は推定されるべきパラメータの組により構造化される。

ここで、N 行 g 列の行列 A = {a _{α
s} } は階数 g で g ≤ N 、h 行 p 列の行列 B = {b _{t i} } は階数 h で h ≤ p であり、共に定数行列である。また、行列 Ξ = { ξ _{s t} } 、 Γ = { γ _{i k} } 、 Λ = { λ _{k m} } 、対称行列 Φ = { φ _{m n} } 、対角行列 Ψ = { δ _{k l} ψ _k } 、及び行列 Υ = { δ _{i j} υ _i } は、パラメータ行列である。

　Jöreskog 自身も指摘しているように、Potthoff & Roy (1964) による一般化 MANOVA (略して、GMANOVA) は、(5.2) 式のみで、(5.1) 式のような共分散行列に関するパラメータ形式を持たない、言い換えれば V ( X ) は定数行列であり、 (5.1) 式のようなパラメータ構造を仮定しない特別のケース、と見ることができる。

　また、例えば (5.1) 式で Γ = I 、及び Υ = O と置けば、明らかにこのモデルは、伝統的な（探索的）因子分析の一般モデルに帰着される。

　このように、共分散構造分析の一般モデルは非常に汎用なモデルと言えるが、一方では大いなる非決定性 (indeterminacy) も持つ（Jöreskog, 1970)。なぜならば、(5.1) 式の Γ を例えば Ω に変換する線形逆変換 T ₁^-1 が存在すると仮定すると、T ₁ Λ T ₂^-1 = Λ ^* 、 T ₂ Φ T ₂ ^t = Φ ^* 、及び T ₁ Ψ ² T ₁ ^t = Ψ ^*2 に対して、(5.1) 式の形は不変であるから。ここで、 Ψ ^*2 は対角行列とし、 T ₂ は逆行列を持つとする。

　そこで、一意的なパラメータの組と対応するそれらの一意的な推定値を得るために、共分散構造分析ではモデルに対する何らかの追加的な制約（幾つかのパラメータをある値に固定したりする）を課することが必要となる。

5.1.3 節　パラメータ構造を構成する２種類のモデル

　(5.1) 式及び (5.2) 式で表される共分散分析のパラメータ構造を構成するモデルは２種類あり、それぞれ測定モデル (measurement model)、構造方程式モデル (structural equation model) と呼ばれる。豊田 (1992) や狩野 (1997) は、両者を測定方程式、構造方程式、と呼んでいるが、ここでは Jöreskog (1989) に従った。

　ここで、前節のデータ行列 X の各行を列に転置したものを、 x と表すとしよう。x は p 行１列のベクトルである。したがって、x _i は被験者 i の p 個の観測変数の値を表すものとする。この時、

測定モデルは、

(5.3)

ここで、x は p次の、u は r次の、 v は s 次の、 e は p 次の確率変数（ベクトル）で、とりわけ e は測定モデルの誤差変数である。また、それぞれの変数の添字 i は、第 i サンプルの値を意味するものとする。すなわち、

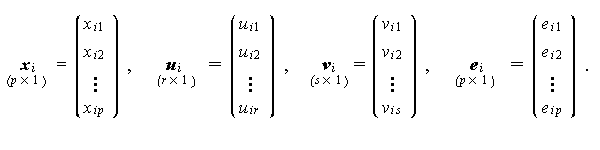
また、ベクトル μ は p 次、行列 L は p 行 r 次、行列 M は p 行 s 次の行列で、順に観測変数の（母）平均ベクトル、潜在変数 u から観測変数 x へのパス係数を要素とする行列、潜在変数 v から観測変数 x へのパス係数を要素とする行列で、

を表す。
これに対して、
構造方程式モデルは、

u _i = F u _i + G v _i + W _i . (5.4)

ここで、行列 F は対角要素が常にゼロの特別な行列である。また、ベクトル u は、原因にも結果にもなるか、結果だけになると仮定される確率変数である。一方、v は原因にのみなる確率変数である。また、w は r 次の（構造方程式モデルの）誤差変数（ベクトル）で、撹乱変数と呼ばれることもある。測定モデルの場合と同様添字 i は第 i サンプルを意味するものとする。

いずれにせよ、(5.4) 式の変数のうち、(5.3) 式で既に定義されている変数以外の変数は、つぎのように定義される：

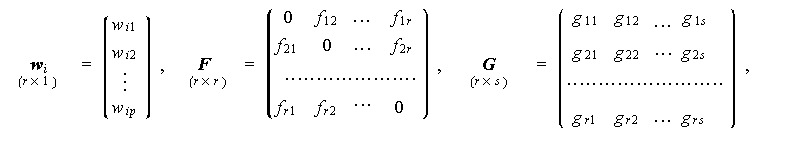
(5.4) 式は、変形するとつぎのようにも書ける：

( I _r - F ) u _i = G v _i + W _i .

(5.5)

ここで、行列 I _r は対角要素がすべて１で非対角要素はすべてゼロの行列、すなわち単位行列である。また、その次数は r である。それ故に、(5.5) 式、従って (5.4) 式のベクトル u は、行列 ( I _r - F ) の逆行列 (inverse matrix)、すなわち ( I _r - F ) ^-1 が存在しないと求めることができないことに、注意したい（逆に、逆行列が存在するような行列は、正則 non-singular と呼ばれる）。すなわち、この仮定は SEM の基本的な仮定の１つで、

SEM の基本的仮定１：　H = I _r - F は正則である。

うえの５種類の変数のうち、観測変数は x のみであり、残りの u、 v 、 e 、 w はすべて潜在変数である。これら潜在変数のそれぞれの平均（ベクトル）は、すべてゼロ（ベクトル）、すなわち以下の仮定がなされる。ここで、これらゼロベクトルの次数は、その下付き添字の値で表した：

SEM の基本的仮定２：
E ( u ) = o _r , E ( v ) = o _s , E ( e ) = o _p , E ( w ) = o _r .	(5.6)

これに対して、μ 、L 、 M 、F、及び G は定数係数の行列（μ はベクトル）であり、 μ は p 次のベクトルで x の期待値ベクトル、L は p 行 r 列の行列で、u _j から x _i への直接的な因果の強さ { l _{i j} } を表す母数、M は p 行 s 列の行列で、v _j から x _i への直接的な因果の強さ { m _{i j} } を表す母数を要素とする行列である。また、F は r 行 r 列の行列で、u _j から u _i への直接的な因果の強さ { f _{i j} } を表す係数を要素とする行列、G は r 行 s 列の行列で、v _j から u _i への直接的な因果の強さ { g _{i j} } を表す係数を要素とする行列である。L 、M 、F、G のうち、F でのみ双方向のパス（指定）が可能である。

共分散構造分析では、変数を外生変数 (exogenous variable) と内生変数 (endogenous variable) に分けることがある。外生変数は、式の右辺にのみ配置される変数を指す。(5.3) 式及び (5.4) 式の変数のうち、 e 、w 、及び v がこれに該当する。これら外生変数内の共分散（行列）を、順に Σ _e 、 Σ _w 、及び Σ _v 、外生変数全体の共分散行列を Σ _exg と書くとすれば、以下の仮定がなされる：

SEM の基本的仮定３：
	(5.7)

ここで、行列 O ₁ は r 行 p 列のゼロ行列、行列 O ₂ は s 行 p 列のゼロ行列、O ₃ は s 行 r 列のゼロ行列である。すなわち、外生変数間では共分散（したがって相関）はすべてゼロであるが、外生変数内での共分散（したがって、相関）は必ずしもゼロでない、と仮定される。一方、内生変数は、式の左辺に配置される変数を指す。(5.3) 式及び (5.4) 式の変数のうち、x 、及び u がこれに該当する。

実は、これら SEM の仮定から付随的に１つの重要な仮定が導かれる。それは、

SEM の付随的仮定：　誤差変数 e と内生潜在変数 u 間では Σ _eu = O ₁^t