|
この節では、まず SEM の各種構造について述べ、統計解析ソフト、主として SAS とそれらの関係について紹介する。
5.1.2 節では、SEM の共分散構造 Σ ( θ ) の1つの表現として、 (5.1) 式で Jöoreskog (1970) によるそれを紹介した。SEM の共分散構造すなわち 共分散のパラメータ構造は、これ以外にも色々な表現が可能である。ここでは、(5.3) 式を多少変形したものを用いて、まず Jöreskog (1970) のそれとは異なるもう1 つの一般的な表現を紹介する。そのために最初に (5.3) 式を以下のように変形し よう:
|
これにより、観測変数(確率変数)y i の期待値(ベクトル)はゼロ(ベクト ル)となる。
これを用いると、SEM の共分散構造はつぎのように表現できる:
|
この式では、観測変数の共分散に関するパラメータ構造 Σ ( θ ) に は内生潜在変数間の共分散構造 Σ u が含まれていないことに注意したい。
Σ ( θ ) は、これら以外にも色々な表現が可能であり、これまでに Bentler and Weeks の EQS モデル (EQuationS model) 、 McArdle and McDonald の RAMモデル (Reticular Action Model)、Jöreskog-Keesling-Wiley の LISRELモデル (LI near Structural RELations model)、McDonald の COSANモデル (COvariance Structure ANalysis model)、 一般化COSANモデル (generalized COSAN model)、など の各構造が提案されている。
これには2種類あり、1つはつぎのように、内生変数(ベクトル) ( y i , u i )t を、それ自身と外生変数(ベクトル) ( e i , w i , v i )t にかかわる部分の和として分解することにより 導かれる Σ ( θ ) のパラメータ構造である:
|
ここで、O 4 は p 行 p 列のゼロ行列、I p 、I r は、それぞれ p 次、r 次の単位行列である。(5.10) 式は、SAS/STAT Software (1997, p.13) では、
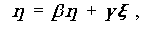 |
(5.11) |
と書かれている。ここで、
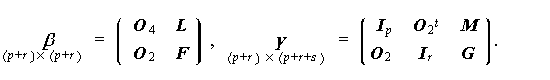 |
(5.10) 式から EQS 構造を導くために、当式をつぎのように y i に関する 式に変形してみよう。
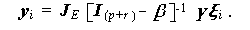 |
(5.12) |
ここで、I (p + r ) は p + r 行 p + r 列の単位行列であり、また
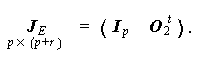 |
(5.13) |
ここで、(5.13) 式を用いると、y i = J E η i と書けることに注意せよ。 もちろん、 η i は (5.11) 式での β に被験者 i の添字をつけた ものである。行列 J E のような行列は、 選択行列 (a selection matrix) と呼ばれる。
さて、(5.12) 式における行列 ( I (p + r ) - β ) は、
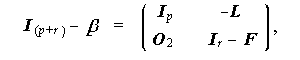 |
(5.14) |
と書けるので、前節で述べた SEM の基本的仮定1から、行列 ( I (p + r ) - β ) もまた正則となる。
いずれにせよ、(5.12) 式から EQS 構造は
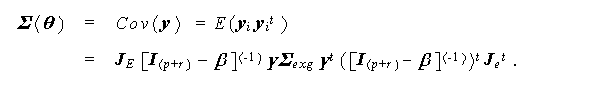 |
(5.15) |
(5.15) 式は、Bentler and Weeks (1980) の オリジナルEQS構造 (original EQS structure) とは多少異なる。
オリジナル EQS モデルでは、SEM の全変数を、それらと外生変数分の2つに分けて 表現する:
|
ここで、O 5 は、( p + r + s ) 行 ( p + r ) 列のゼロ行列、O 6 は ( p + r + s ) 行 ( p + r + s ) 列のゼロ行列である。
この時点で、(5.16) 式の右辺第1項の係数行列と、第2項の係数行列とをそれぞれ、 つぎのように書くとする:
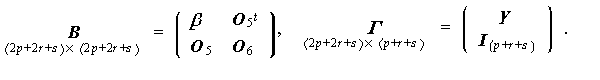 |
これらは、SAS/Stat Software (1997, p.13) の行列 B 及び Γ に他な らない。
つぎに、(5.13) 式と同様な行列を
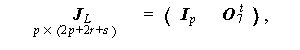 |
(5.17) |
と定義し、η i や ξ i を新たに
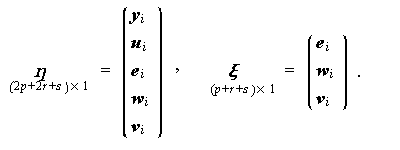 |
とおけば、y i = J L η i = J L ( I (2p + 2r + s ) - B )-1 Γ ξ i と書けることに注意せよ。O 7 は (p + 2r + s ) 行 p 列のゼロ行列 である。ここで、( I (2p + 2r + s ) - B ) も、(5.14) 式と同様、正則となる。 これを用いると、オリジナル EQS 構造は、つぎのように書ける:
|
この式の右辺は、SAS/STAT Software (1997, p.13) の LINEQS の行列 C に他 ならない。結局、EQS (LINEQS) では、うえで定義した4種の行列 J L 、B 、 Γ、 Σ exg のうち、 J L を除く3つの行列を指定すれば よい。
EQS 構造では、観測変数 y の共分散構造 Σ( θ ) を定数行列 J L を除く3種の行列で表現するのに対して、RAM 構造ではそれを2種の行列で 表現する。まず、SEM はつぎの形にまとめられる:
|
ここで、O 8 は s 行 s 列のゼロ行列である。
ここで、(5.19) 式の右辺第1項の係数行列を
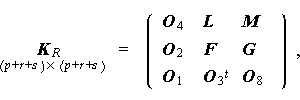 |
(5.20) |
と置き、さらに (5.13) 式や (5.17) 式と同様、行列 J を
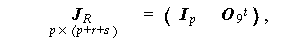 |
(5.21) |
と置くと、y i = J R η i = J R [ I (p + r + s ) - K R ]-1 η i と書けることに注意しよう。ここで、この場合はもちろん η i = ( y it , u it , v it )t である。また、(5.21) 式の行列のうち、 O 9 は r + s 行 p 列のゼロ行列である。
これより、RAM 構造はつぎのように書ける:
|
(5.22) 式の右辺は、SAS/STAT Software (1997, p.13) の RAM モデルにおける共分散 構造 C に他ならない。明らかに、RAM 構造の場合、われわれは K R と Σ exg の2種を指定すればよい。
LISREL では、測定モデルの観測変数を2種類仮定する。すなわち、(5.8) 式を 2つに分けて、
|
と仮定する。言い換えれば、観測変数 y を、内生変数 u により説明でき るものと外生変数 v により説明できるものの2つに分解する。ここで、上式で p 1 + p 2 = p であるとする。
これら2本の方程式は、つぎのように書くのと同等である:
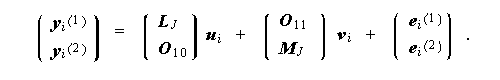 |
(5.25) |
ここで、(5.25) 式の右辺の2つのゼロ行列 O 10 及び O 11 は、 それぞれ、p 2 行 r 列、p 1 行 s 列から成る。
この時、LISREL の方程式はつぎのように書ける:
|
ここで、(5.26) 式の右辺第1項の係数行列を
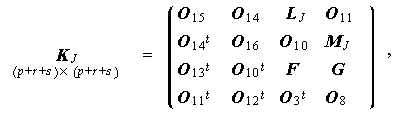 |
(5.27) |
と置き、さらに (5.13) 式、 (5.17) 式や (5.21) 式と同様、行列 J を
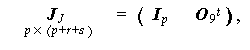 |
(5.28) |
と置くと、y i = J J η i = J R [ I ( p + r + s ) - K J ]-1 ξ i と書けることに注意しよう。ここで、この場合はもちろん、 η i = ( y i(1)t , y i(2)t , u it , v it )t である。また ξ i = ( e i(1)t , e i (2)t , w it , v it )t である。
これより、LISREL 構造はつぎのように書ける:
|
ここで、うえの式の右辺の行列 Σ exg(J ) は、次の通りである:
|
(5.29) 式及び (5.30) 式は、SAS/STAT Software (1997, p.14) の行列 C 及び P にあたる。結局、LISREL では2種の行列 K J 及び Σ exg(J ) を指定すればよい。SAS の CALIS プロシジャには、LISREL 用の特別な入力方法はないが、COSAN、LINEQS、あるいは RAM 文により、指定可能 である。
これまで見てきた EQS、RAM、LISREL 構造は、すべて McDonald (1978, 1980) の オリジナル COSAN モデル における共分散構造
|
の特殊形になっている。
SAS の CALIS プロシジャでは、うえの COSAN 構造をさらに一般化した 一般化 COSAN model による一般化 COSAN 構造
|
を扱うことが可能である。