5.2.2 節 SAS による各種構造の解析概要

SAS では、CALIS プロシジャが SEM を実行する。この節では、SAS/STAT Software (1997) に従って、CALIS プロシジャの概要と、２、３の応用例をまとめる。

5.2.2.1 節　CALIS プロシジャの特色

CALIS プロシジャの特色を列記すると、つぎのようである：

• CALIS プロシジャの仮定と推定法

  - 分布の仮定

  　SEM では、確率変数はすべて近似的に多変量正規分布に従うと仮定する。一方 サンプル数が十分大きいときは、Browne の 漸近的に分布によらない推定法 (Asymptotically distribution free estimation)（略して ADF 推定法）が使 える。

  - パラメータの推定法

  SAS では、SEM のパラメータの推定方法として、

  ＊　重みなし最小二乗法 (unweighted least squares, ULS) 　　

  ＊　一般化最小二乗法 (generalized least squares, GLS) 　

  ＊　最尤法 (maximum likelihood)

  ＊　重みつき最小二乗法 (weighted least squares, WLS, ADF)

  ＊　対角重みつき最小二乗法 (diagonally weighted least squares, DWLS)

• CALIS の各種文による各種分析方法

  - FACTOR 文

  　制約付き（確認的）因子分析又は（主）成分分析 (constrained (confirmatory) factor analysis or component analysis)

  - RAM 文

  　単純パス解析 (simple path models)

  - LINEQS 文

  　Benlter (1985) 型の EQS 構造による SEM

  - COSAN 文、MATRIX 文

  　McDonald and Fraser 型の COSAN 構造による SEM

  - FACTOR 文

• CALIS による多標本データの分析
  　CALIS では、サンプルサイズが等しい多標本データの分析のみ可能。

• CALIS による各種分析モデルの例
  　CALIS プロシジャは、McDonald (1978, 1980) のオリジナル COSAN を 一般化した一般化 COSAN モデルを扱うが、それによるモデルの具体例と して上記テキストでは以下を挙げている：
  1. オリジナル COSAN
  2. RAM モデル
  3. LINEQS（オリジナル EQS）
  4. LISREL モデル
  5. 階層的因子分析モデル (hierarchical factor analysis model)
     　一次モデル： Σ _y ( θ ) = P Σ P^t + U
     　二次モデル： Σ _y ( θ ) = P ₁ P ₂ Σ P ₂^t P ₁^t + P ₁ U ₂² P ₁^t + U ₁² .
  6. 一次自己回帰的縦断的因子モデル, McDonald (1980)

5.2.2.2 節　パス図の例１

ここでは、SAS/STAT Software (1997, p.16) に掲載されている Wheaton, et al. (1977) の パス図 (pass diagram) の例を示す。データは、９３２名の被験者 に対して施された６変数（観測内生変数）：

1. anoms:　1967 年時点での失名詞 (anomia) 傾向

2. powls:　1967 年時点での無気力感 (powerlessness)

3. anomo:　1971 年時点での失名詞 (anomia) 傾向

4. powlo:　1971 年時点での無気力感

5. yschl:　教育年数 (education/years of schooling)

6. seind:　社会・経済的指標 (Duncan's Socioeconomic index)

1. fend1:　1967 年時点での疎外感 (alienation)

2. fend2:　1971 年時点での疎外感

1. fexo1:　社会経済的地位 (socioeconomic status)

また、上記観測内生６変数の誤差項を順に、E1、E2、E3、E4、E5、E6 とし、潜在 内生２変数の誤差項（撹乱項）を順に、D1、D2 と書くものとする。図 5.1 は、 上記 Wheaton et al. (1977) のパス図の表現を多少修正したものである。

以降、パス図では図 5.1 と同様に、観測（内生）変数のみ矩形の枠で囲むものと する。したがって、矩形の枠以外の枠（円や、楕円様の枠）で囲まれた変数は各種 変数（内生潜在変数、外生潜在変数、（外生）誤差変数、（外生）撹乱変数）を 表す。また、外生潜在変数については、内生潜在変数と簡単に見分けがつくように、 太い楕円様の枠で囲むことにする。

図 5.1 からは、Wheaton et al. (1977) のデータでは、被験者の（外生潜在変数 である）社会経済的地位 (fexo1) が、（２つの内生潜在変数である）1967 年時点で の被験者の疎外感 (fend1) や同 1971 年時点での疎外感 (fend2)、及び６つの観測 変数のうちの２つである教育年数 (yschl) や社会・経済的指標の原因となっている こと、２つの内生潜在変数である２時点での被験者の疎外感のうち前者が後者の原因 となっていること、さらには前者が 1967 年の時点での（観測変数としての）失名詞 (anoms) や無気力感 (powls) の、後者が 1971 年の時点での（観測変数としての） 失名詞 (anomo) や無気力感 (powlo) の原因である、という仮説が立てられている ことがわかる。

図5.1 : Wheaton らのパス図

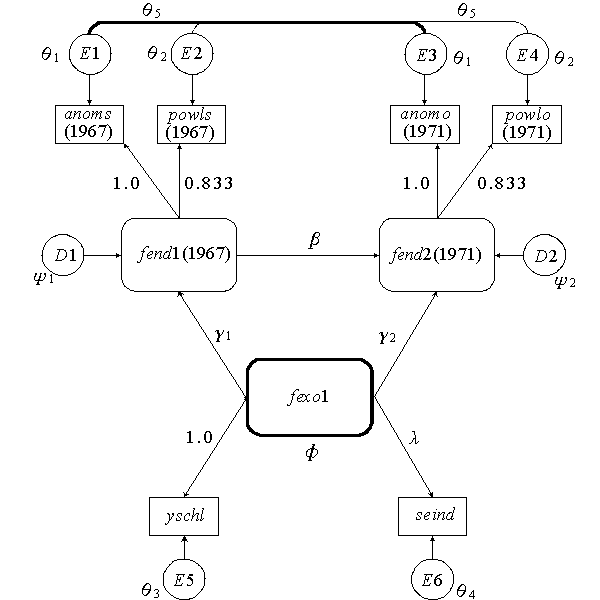ここで、図中、パスの近傍に表示してあるパス係数のうち、数値で具体的 に示されているのは何らかの仮説や過去の知見から既知のパラメータ（ 固定母 数 fixed parameters）であること、ギリシャ文字で表されているものは、（データ から値を推定すべき）未知のパラメータで、自身以外の変数との何の制約もないも の（ 自由母数 free parameters）か、さもなければ他の変数との制約関係にある もの（ 制約母数 constrained parameters) であること、に注意したい。 図 5.1 では、各観測変数の誤差を意味する誤差変数 E1 , E2 , ... , E6 の誤 差分散は、失名詞については２時点で等しい（共に、θ ₁ ）、無気力感につい ても同様であること（共に、θ ₂ ）や、失名詞についても無気力感についても ２時点間の共分散は等しい（共に、θ ₅ ）ことなどが仮定されていることも わかる。これらは、上の分類からは制約母数に入れられる。