ここでは SAS の CALIS について、前節の Wheaton et al. (1977) 等の具体例を 用いて、各種共分散構造ごとに SEM のパラメータを指定する方法を解説する。
| Wheaton データの LINEQS モデル文による SEM プログラムの例 |
5.2.1 節の EQS 構造のところで述べたように、観測変数の共分散行列のパラメータ 構造を EQS 構造、とりわけオリジナル EQS 構造で表現すると、(5.18) 式により 表されるので、われわれは行列 B 、Γ、及び Σ exg の 各要素を指示すればよい。 SAS では、EQS 構造を用いて SEM のパラメータ指定を 行う場合には、LINEQS モデル文、STD 文、COV 文などを用いる。
とりわけそれらのうち LINEQS 文は、そのための中心的な文で あり、これらの要素のうち、内生変数(観測変数と内生潜在変数)に関する方程式 (行列 B 、Γ がそのための情報を持つ)を記述するためのものであ る。
LINEQS モデル文の一般形は、つぎの通りで
LINEQS
dependent = term + term + ... ,
dependent = term + term + ... ,
................
dependent = term + term + ... ;
|
と書く。ここで、dependent ... の各行の最後のコンマを忘れないこと。また、最後の dependent ... の最後にセミコロンがあるが、これも忘れないこと。これは LINEQS 文の末尾を意味する。dependent には、観測内生変数名及び潜在 内生変数名をすべて列記する必要がある。
また、各 term は、以下の3つのうちのいずれかでなければならない:
|
ここで、上記の name はすべて SAS 名なので、8文字以内である必要がある。 また、SAS では SEM の変数名としての SAS 名に、以下のような制約があるので、 これらの制約に従う必要があるので、注意が必要である:
図5.1 の例では、図中の自由母数のうち、λ , γ 1 , γ 2 , β に対して、それぞれ順に LAM、GAM1、GAM2、BET なる SAS 名を付けるとして、対応 する (5.8) 式と (5.4) 式を、被験者用の下付き添字 i を除き、順にスカラー表 現すると、つぎのようになる。この場合にも、変数名は上の制約に従っていることを 確認するとよい:
LINEQS
anoms = fend1 + E1,
powls = .833 fend1 + E2,
anomo = fend2 + E3,
powlo = .833 fend2 + E4,
yschl = fexo1 + E5,
seind = LAM (.5) fexo1 + E6,
fend1 = GAM1(-.5)fexo1 + D1,
fend2 = BETA(.5) fend1 + GAM2(-.5)fexo1+ D2;
|
読者は、たとえ行列の計算はわからなくても、図 5.1 とこの方程式を見比べれば、 LINEQS モデル文の方程式の指定は可能であろう。
一方、EQS 構造の Σ exg(すなわち、外生変数)に関する情報を指示 するために、LINEQS モデル文では STD 文と COV 文をも用いる。前者の STD 文では、 3種の外生変数 e(観測変数の誤差)、w(内生潜在変数の誤差)、v (外生潜在変数)の分散のうち、どの分散をパラメータとして推定推定するの かを指示する。STD となっているが、それにより指定する値は標準偏差 ではなく分散である。
STD 文の一般形は、つぎの通りである:
STD
variables = pattern-definition,
variables = pattern-definition,
................
variables = pattern-definition;
|
ここで定義されない変数の分散はゼロであるとみなされる。図 5.1 の場合、観測 変数の誤差項の分散 θ 1 , θ 2 , θ 3 , θ 4 を順に THE1、 THE2、THE3、THE4 なる SAS 名、撹乱変数 D1、D2 の分散 ψ 1 、ψ 2 を PSI1、PSI2 なる SAS 名、外生潜在変数 fexo1 の分散 φ を PHI なる SAS 名 を付けるとすると、STD 文はつぎのようになる:
STD
E1-E6 = THE1 THE2 THE1-THE4 (6*3.),
D1-D2 = PSI1 PSI2 (2*4.),
fexo1 = PHI (6.);
|
同じく COV 文は、Σ exg の要素のうちの共分散、とりわけ3種の外生 変数(観測変数の誤差、内生潜在変数の誤差、及び外生潜在変数)のそれぞれの(複 数の)変数内共分散のうち、どれをパラメータとして推定すべきで、どれを固定する かを指定するためのものである。ここで定義されない要素は、ゼロとみなされる。
COV 文の一般形は、つぎの通りである:
COV
variables <* variables 2> = pattern-definition,
variables <* variables 2> = pattern-definition,
................
variables <* variables 2> = pattern-definition;
|
COV 文の各「variables ...」の左辺に * 記号を付けるやり方は リスト間共分 散 (Between-List Covariances)、 * 記号を付けないやり方は、 リスト内共分 散 (Within-List Covariance) と呼ばれる。
例えば、
COV E1-E4 = PHI1-PHI6; |
は、リスト内共分散の定義をしたことになり、
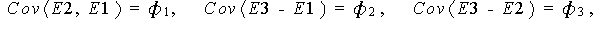 |
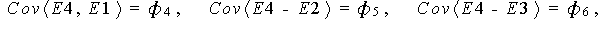 |
一方、
COV E1-E2 * E3 E4 = PHI1-PHI4; |
は、リスト間共分散の定義をしたことになり、
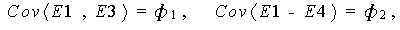 |
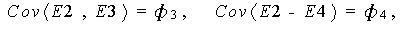 |
図 5.1 の場合、COV 文はつぎのように書く:
COV
E1 E3 = THE5 (.2),
E2 E4 = THE5 (.2);
|
Wheaton et al. (1977) のデータについて、lineqs 文のみでなく、CALIS プログラム 全体を示すと、つぎのようになる。このプログラムは、SAS/STAT Software (1997, pp.143-144) の一部をこのテキスト用に修正したものである:
data Wheaton(type=cov);
title "Stability of Alienation";
title2 "data matrix of Wheaton, Muthen, Alwin & Summers (1977)";
_type_ ='cov';
input _name_ $ anoms powls anomo powlo yschl seind;
label anoms='Anomia (1967)'
powls='Powerlessness (1967)'
anomo='Anomia (1971)'
powlo='Powerlessness (1971)'
yschl='Education'
seind='Occupational Status Index';
cards;
anoms 11.834 . . . . .
powls 6.947 9.364 . . . .
anomo 6.819 5.091 12.532 . . .
powlo 4.783 5.028 7.495 9.986 . .
yschl -3.839 -3.889 -3.841 -3.625 9.610 .
seind -21.899 -18.831 -21.748 -18.775 35.522 450.288
;
proc calis data=Wheaton cov tech=nr edf=931 pall;
lineqs
anoms= f1 + e1,
powls= .833 f1 + e2,
anomo= f2 + e3,
powlo= .833 f2 + e4,
yschl= f3 + e5,
seind= lamb (.5) f3 + e6,
f1=gam1 (-.5) f3 + d1,
f2= beta (.5) f1 + gam2 (-0.5) f3 + d2;
std
e1-e6=the1-the2 the1-the4 (6*3.),
d1-d2=psi1-psi2 (2*4.),
f3=phi (6.);
cov
e1 e3=the5 (.2),
e4 e2=the5 (.2);
run;
|
| sem-Wheaton-lineqs.sas |