|
一般に、あるモデルに 識別性 (identifiability) があるかどうかということは、 モデルの未知パラメータが既知データから一意的に決定できるか、という問題である。 SEM の場合、より正確に表現すると、モデルが識別されるということは、
|
が成り立つことである。
豊田 (1992) では、SEM のモデルの既知数、すなわち観測変数間共分散行列 S もしくは同相関行列 R の既知数 { p + p ( p - 1)/2 = p (p + 1)/2 } と、識別性を得るための制約数 n c(自由母数と制約母数の数の和)との差の問題 に重心が置かれているが、狩野 (1997) では Jöreskog (1969) 等にあるモデル 自身の線形変換による識別性のなさとパラメータ数によるそれの両方を明確に指摘 している。一方、豊田では狩野にはない詳細な識別性の具体的かつ理論的記述があり、 このテキストでは豊田 (1992) をまとめる。
ここでは、SEM の線形変換による識別性のなさを、5.1.2 節で述べた Jöreskog (1970) のやり方でなく、豊田 (1992) の表現を用いて示す:
まず、SEM の構造方程式モデル (5.4) 式を、5.1.3 節で述べた SEM の基本的仮定1 で用いた行列 H を用いて、 u i = H -1 ( G v i + w i ) と 置き、測定モデルの1つの表現である (5.8) 式に代入して整理すると、
| y i = ( LH -1 G + M ) v i + LH -1 w i + e i , | (5.37) |
と書ける。
さらに、5.1.3 節で述べた、(1) SEM の基本的仮定3、言い換えれば Σev 、 Σew 、及び Σvw が共にゼロ行列であること、及び (2) SEM の付随的仮定すなわち Σeu もゼロ行列であること、を用いると、SEM の 共分散構造は、つぎのように整理できる:
 |
(5.38) |
この式は、(5.9) 式で左辺の行列に添字 y を付けただけで、(5.9) 式そのものと 言っても差し支えない。
ここで、構造方程式モデルの潜在変数 u i 、v i 、及び w i を正則な 一次変換行列 T 1 (次数 r )、 T 2 (次数 s )、及び T 1 により u i =T 1 u i* 、 v i =T 2 v i* 、 及び w i = T 1 w i* のように変換するとする。これらにより、y i はつぎのようになる:
| y i = ( LH -1 G + M ) T 2 v i* + LH -1 T 1 w i* + e i . | (5.39) |
うえの y i を用いて Σy ( θ ) を計算し直すと、つぎのように 書ける:
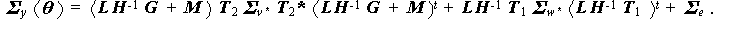 |
(5.40) |
ここで、変換 v i =T 2 v i* 、 及び w i =T 1 w i* により、 行列 Σv や Σw が
 |
(5.41) |
と書けることに注意すると、潜在変数 u i 、v i 、及び w i の正則 一次変換に対して、SEM の共分散構造 Σy ( θ ) は不変であることが わかる。
結局、この一般的な識別性のなさを解消するために、SEM では F 、G 、 L や M や、潜在変数 u i 、v i 、及び w i がらみの共分散 構造あるいは e i の幾つかを固定することにより、制約を課すのである。した がって、SEM の解が意味を持つためには、これらの制約自身が実証的なデータや経験 に基づき十分妥当なものである必要があろう。
構造方程式モデルの母数は、すべて内生潜在変数の共分散行列 Σu の中に 現れるので、構造方程式モデルの識別性は
|
と書ける。
ここで、u i の定義から Σu を計算すると、
|
ここで、H = I - F 。
(5.43) 式より、Σu ( θ ) は H (したがって F )、 G 、Σv 及び Σw により決定されることに注意。これらの うち、Σv (及び Σu と Σuv )は構造方程式モ デルの識別性を論じるときには既知と仮定されるので、 θ が識別できるた めには残りの F 、G 、及び Σw が識別できればよい。
以下の4つの条件は、これらにかかわるものである:
| 構造方程式モデルが識別されるための1つの 十分条件は、F のすべ ての要素が固定母数であることである。 |
このことを証明するには、うえの議論から、この条件により G と Σw が識別されることが証明できればよい。まず、前者については、SEM の仮定より Σuv = E ( u i v it ) = FΣuv + GΣv が成り立つ ことに注意しよう。これより、
 |
(5.44) |
ここで、(5.44) 式の右辺の Σuv と Σv は、既知との仮定 があるので、F が固定されていれば、G は決まることがわかる。
つぎに、Σw は (5.43) 式を用いて、
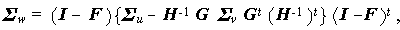 |
(5.45) |
と書けるので、やはり F が固定されていれば決まる。
Wheaton et al. (1977) の例では、(5.33) 式の F にあたる部分(あるいは、 図 5.1 の内生潜在変数間のパス係数)を見れば明らかなように、F 固定条件 が満たされていない。
ただし、F 固定条件は 十分条件 なので、これが満たされていなくても 当該モデルが識別される可能性はあることに注意したい。
一方、Thurstone データの例では、(5.35) 式の F の部分(あるいは、図 5.2 の内生潜在変数間の関係)を見れば明らかなように、( F の要素はすべて ゼロと固定されていると見れるので)F 固定条件は満たされている。
| 構造方程式モデルが識別されるための1つの 十分条件は、F が下(上) 側三角行列で、かつ Σw が対角行列であることである。 |
ここで、逐次条件とは関係なく F が下(上)側三角行列だと、H は必ず 正則になることに注意。
逐次条件は、言い換えると、 内生潜在変数間では双方向の因果はなく、 また内生潜在変数間の誤差は互いに無相関である、という仮定に他ならない。SEM では一般に外生潜在変数 e 、w 、v 間は互いに無相関と仮定するが、 それ以外では相関はあってもなくてもよい、ことに注意せよ。この点では、逐次条件 は、それらの1つの相関がない、とする特別な仮定であると言える。
最後に、(1) の F 固定条件では Σw の対角行列条件は不要であった ことに注意せよ。
Wheaton et al. (1977) の例では、F については (5.33) 式を、Σw については (5.34) 式のそれぞれの該当個所(あるいは、図 5.1)を見れば明らかな ように、逐次条件は満たされている。
Thurstone データの例では、(5.35) 式の F の部分( F の要素はすべて ゼロと固定されており、下(上)側三角行列の特殊ケースとみれる)(あるいは、 図 5.2 の関係)を見れば明らかなように、逐次条件は満たされている。
| 構造方程式モデルの r 個の方程式のうち、第 i 番目が識別されるための 1つの 必要条件は、Σw に制約がないという条件下で}、 行列 ( I - F , -G ) の第 i 行の要素が r - 1 個以上のゼロを含むこと である。 |
この条件は必要条件なので、これが満たされないとモデルは識別できないことに 注意せよ。
例1. 架空の例
つぎのような架空の構造方程式モデルを例に取れば、
|
行列 ( I - F , -G ) は、つぎのように書ける:
 |
(5.47) |
この行列は、各行共2つずつゼロを含むので、もし Σw に制約 がなければ(言い換えると、すべて自由パラメータから成るとすれば)、3つの方程 式は共に次数条件を満たす。
例2. Wheaton et al. (1977) の例
Wheaton et al. のデータでは、
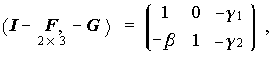 |
(5.48) |
となり、第1番目の方程式は次数条件を満たすが、第2番目のそれは満たさないことが わかる。しかし、このデータのモデルの場合、Σw に制約がある(非対角 要素がゼロ、という制約)ので、この条件の議論外にある。
一方、Thurstone データでは、
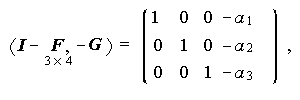 |
となり、各行共2つのゼロを含むので、もしΣw に制約がなければ、次数 条件が満たされる。しかし、このデータでは Σw に対して、対角要素は1、 非対角要素はゼロ、という制約を設けているので、この条件の議論外にある。
| 構造方程式モデルの i 番目の方程式が識別されるための 必要十分条件は、 Σw に制約がないという条件下で、行列 ( I - F , -G ) に関して、第 i 行の要素がゼロでない列と第 i 行目を削除した時 の行列のうち、行列式がゼロでないものが少なくとも1つ存在する、ということで ある。 |
上記の例1の場合には、各行の i 行目の要素がゼロでない列と、第 i 行自身を 削除した行列を Ci とすると、
 |
となり、γ 11 も γ 22 もゼロでないので、これらすべての行 列の行列式はゼロでない。したがって、例1の構造方程式モデルの各行は、もし Σw に制約がなければ、階数条件を満たす。
例2の Wheaton et al. の例では、C 1 =1 となる。しかし、C 2 は、その 第2行目の要素にゼロがないので、構成できない。つまり万が一Σw に 制約がなければ、第2番目の方程式は階数条件を満たさない。 ただし、この階数条件は Σw に制約がないという条件のもとでのもので あるが、Wheaton et al. のモデルでは、Σw に制約がある(非対角要素 がゼロ、という制約)ので、この条件の議論外にある。
観測変数間の共分散構造 Σy ( θ ) は、EQS、RAM、LISREL 構造等 における表現 Σ ( θ ) ((5.18) 式、(5.22) 式、(5.29) 式等)以外 にも、つぎのように書くことができる:
|
ここで、(5.49) 式を導くに際しては、Σeu = E ( e i u it ) より、 Σeu ( I - F )t = O 2t であること及び ( I - F ) が正 則であることから、Σeu = O 2t 、すなわち 5.1.3 節で述べた「SEM の付随的仮定」が成り立つことに注意。
そこで、測定モデルの識別性は、(5.49) 式の Σy ( θ ) に対して、
|
が成り立つことである。
ここで、簡単のために (5.49) 式の一部を以下のように書き換える:
 |
|
Wheaton et al. (1977) のモデルでは、(5.33) 式の右辺の部分行列 L と M が行列 A を構成するので、ごれらを見ると3重指標条件の4つの条件のうちの (a) は満たされていることがわかる。しかし、明らかに (b) は満たされていない。ま た、(5.34) 式の右辺の部分行列 Σe を見れば明らかなように、(c) も満 たされていない。最後の (d) は満たされている。したがって、このモデルは3重指標 条件を満たさない。
Thurstone データのモデルでは、(5.35) 式や図 5.2 より、明らかに (a)、(b)、 (c) は満たされている。(d) については、内生変数は3つとも A に1つ以上の 固定母数を持つという条件は満たしていないが、ΣM の当該対角成分(すな わち、分散)がすべて固定母数(1.0)であるから、3重指標条件は満たされている。
|
測定モデルが識別されるための1つの 十分条件は、3重指標条件が成り
立ち(ただし、その (2) については、A の各列に3つ以上でなく2つ以上の
ゼロでない母数がある、でよい)、さらに (e) ΣM の下側三角要素の各行各列に1つ以上のゼロでない母数がある、 が成り立つことである。 |
Wheaton et al. (1977) のモデルは、3重指標条件が成り立たないので、2重指標 条件も成り立たないことは明らかである。
一方、Thurstone データの場合、3重指標条件は満たされているが、内生潜在変数 と外生潜在変数間にも相関を仮定していないので、(e) が満たされない。したがって 2重指標条件は満たされない。
3重・2重指標条件が、測定モデル全体に対する識別性の条件であるのに対して、 1指標条件は 特定の構造的潜在変数(第 j 番目のそれ)を測定する観測変 数が1つしかない時(これが y i であるとする)の、当該潜在変数の識別性の条件 である:
|
Wheaton et al. (1977) の例では、潜在変数を測定する観測変数はすべて2つある ので、この条件に該当しない。Thurstone データの場合も同様である。
 、Σe の第 (i, i) 要素を
(1 - ρ i ) s i2 とする。
、Σe の第 (i, i) 要素を
(1 - ρ i ) s i2 とする。(b) の方法の長所は、(a) に比べて観測変数の測定誤差を考慮している点である。
これまでに述べてきた条件は、構造方程式モデルと測定モデルを別々に扱ってきたが、 両モデルを合わせた識別条件は、
|
Wheaton et al. (1977) のモデルでは、構造方程式モデルのみが識別可能であった。 実際の分析場面では、必要条件は満たすが十分条件は満たさないモデルの分析を行 わねばならない場合が多い。