5.4 節　分析結果の評価

　SEM では、最初に構成したモデルが最適なものかどうかはわからない。例えば、 分散の推定値が負になったり、推定共分散行列が正定値にならない、等、モデルの 仮定を満たさない結果がえられたならば、モデルを再検討しなければならない。

　また、明らかな欠点が表面上は見られなくても、一回の計算で分析を終了すること は、危険である。むしろ、分析結果をもとにモデルを再構成、再分析を繰り返すこと により、よりよいモデルを見つけなければならない。

　SEM におけるモデルの改良には、モデルの全体的評価と部分的評価がある。分析 は通常、まずモデルの全体的評価を行い、モデルのデータへの適合性を評価し、うま く適合していないときは、母数、変数、方程式などの部分的評価を個々に行い、適合 の悪い箇所を見つけモデルを修正し、再度全体的評価をする、という手順を繰り返す ことが多い。

5.4.1 節　モデルの全体的評価

　SEM モデルの全体的評価の方法は、たくさんのものが知られている。以下に代表的 なもののみを示す。

5.4.1.1 節　χ² 検定

SEM では、帰無仮説

を、対立仮説

に対して検定する。心理学の分野での多くの検定においては、心理学的（作業）仮説 は帰無仮説が棄却された時に正しい場合が多い。すなわち、例えばわれわれは、ミラー リエル錯視SEM では逆である。

ここで、データ S に対するモデル Σ( θ ) の適合度関数 f に 対して、次の量

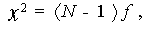(5.51)

は、N が大きい時近似的に自由度

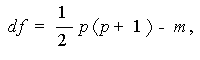(5.52)

なる χ² 分布に従う。ここで、(5.52) 式の m は、

である。