第4章 ニューロンの発火モデル
![]()
![]()
| 4.1 ニューロンの発火モデルの研究の歴史 |
| 4.2 積分発火モデル |
| 4.3 発火率モデル |
| References |
この頁は、平成28年7月18日に新たに開設しました。
この頁は、令和2年5月18日に一部更新しました。
![]()
4.1 ニューロンの発火モデルの研究の歴史
ニューロンの発火モデルは、ニューロンの発火についての McCulloch and Pitts (1943) に
さかのぼる。最近では Cannon et al. (1983), Bernander et al. (1991), van Vreeswijk and
Sompolinsky (1996), Salinas and Sejnowski (2002) などがある。
Kandel et al. (2013) によれば、積分発火モデル (integrate-and-fire model) では、つぎの仮定を置く:
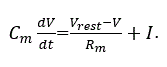
|
(1) |
ここで、Cm は膜容量、Rm は膜抵抗、Vrest はニューロンの 静止電位である。
Kandel et al. (2013) によれば、ニューロンとそれらの間の相互作用が発火率により記述される ネットワークでの1つ目の要素は、ニューロンが受け取る全シナプス電流 I とニューロンの発火率 との関係である。定常電流に対しては、この関係は発火率関数 r=F(I) によって与えられる。
電流が時間とともに変動する場合、発火率は遅延を伴い時定数τで指数関数的にこの関数に近づく と仮定すると、
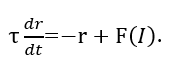
|
(2) |
2つ目の要素は、I とネットワークの他のニューロンとの関係である。ここでは、2つの 細胞集団からなるネットワークを仮定する。さらに、興奮性ニューロンの集団はすべて発火率 rE、抑制性ニューロンの集団はすべて発火率 rI で発火すると仮定す る。また、これら2つの集団への外部入力が hE および hI とする。 一方、2種類の集団間のシナプス結合強度は4種類を仮定する。それらは、WEE、 WII、WIE、WEI とする。このとき、2つの集団の対応する ニューロンそれぞれの発火率の変化は
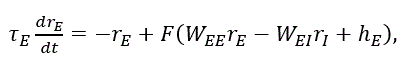
|
(3) |
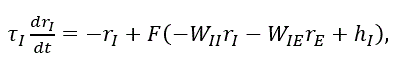
|
(4) |
微分方程式 (differential equation) で記述される。両式は、関数 F が 非線形であれば、非線形一階微分方程式系である。
Kandel et al. (2013) によれば、ニューロンとそれらの間の相互作用が発火率により記述されるネットワークでの
甘利俊一・外山敬介 (2000). 脳科学大事典 朝倉書店
Sato, M. (1990). A learning algorithm to teach spatiotempral patterns to recurrent neural networks. Biological Cybernetics, 62, 259-263.
Sato, M., & Murakami, Y. (1991). Learning nonlinear dynamics by recurrent neural networks. Proceedings of Symposium on some problems on the theory of dynamical systems in applied science, pp.49-63. World Scientific.